UStepper Robot Arm 4: 5 Βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:34

Αυτή είναι η 4η επανάληψη του ρομποτικού μου βραχίονα, το οποίο έχω αναπτύξει ως εφαρμογή για τον πίνακα ελέγχου stepper της uStepper. Δεδομένου ότι το ρομπότ διαθέτει 3 βηματικούς κινητήρες και ένα σερβο για ενεργοποίηση (στη βασική του διαμόρφωση) δεν περιορίζεται στο uStepper, αλλά μπορεί να χρησιμοποιηθεί με οποιονδήποτε πίνακα οδηγών stepper.

Ο σχεδιασμός βασίζεται σε ένα βιομηχανικό ρομπότ παλετοποιητή - και είναι σχετικά απλός. Τούτου λεχθέντος, έχω περάσει αμέτρητες ώρες για να σχεδιάσω και να το βελτιστοποιήσω τόσο για ευκολία συναρμολόγησης, όσο και για ευκολία εκτύπωσης των εξαρτημάτων.

Έκανα το σχέδιο με γνώμονα την ευκολία εκτύπωσης και την απλότητα συναρμολόγησης. Όχι ότι δεν υπάρχει τρόπος βελτίωσης σε αυτές τις δύο παραμέτρους, αλλά νομίζω ότι έχω προχωρήσει πολύ. Επιπλέον, θα ήθελα να κατεβάσω τη βιομηχανική ρομποτική σε ένα επίπεδο όπου οι χομπίστες μπορούν να την ακολουθήσουν δείχνοντας ότι μπορεί να γίνει σχετικά απλό - επίσης τα μαθηματικά για να το ελέγξουν!

Μη διστάσετε να αφήσετε ένα σχόλιο με εποικοδομητική ανατροφοδότηση τόσο για το σχέδιο, όσο κυρίως για τον τρόπο με τον οποίο το κάνω προσβάσιμο σε όλους (ειδικά στα μαθηματικά).

Βήμα 1: Απαιτούμενα μέρη, τρισδιάστατη εκτύπωση και συναρμολόγηση

Βασικά όλα όσα πρέπει να γνωρίζετε βρίσκονται στο εγχειρίδιο συναρμολόγησης. Υπάρχει ένα λεπτομερές BOM με αγορασμένα και τυπωμένα μέρη και μια λεπτομερής οδηγία συναρμολόγησης.

Η τρισδιάστατη εκτύπωση γίνεται σε λογικής ποιότητας τρισδιάστατο εκτυπωτή (FDM) με ύψος στρώματος 0,2 mm και 30 % πλήρωση. Μπορείτε να βρείτε την τελευταία επανάληψη ανταλλακτικών και οδηγιών εδώ:

Βήμα 2: Κινηματική

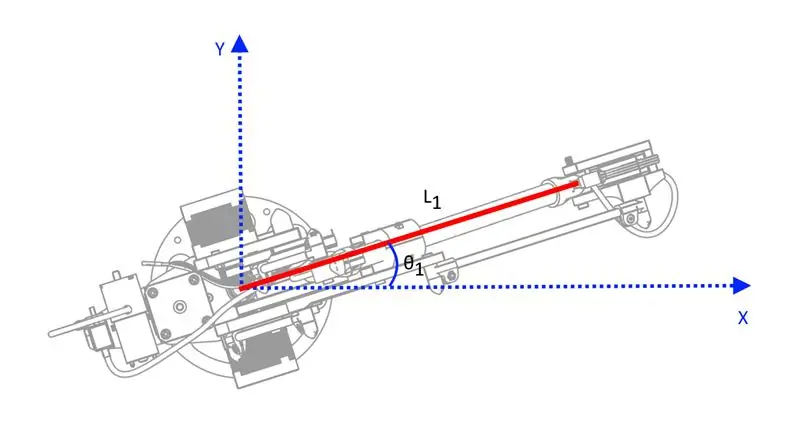
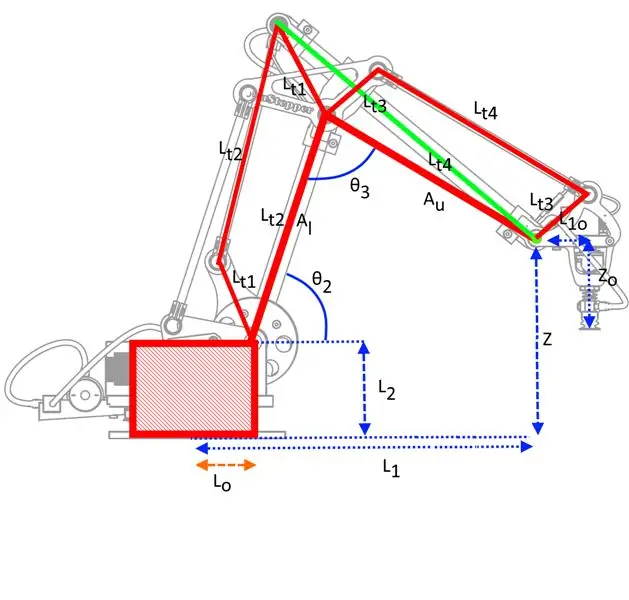
Για να κάνετε το χέρι να κινείται με τον προβλέψιμο τρόπο, πρέπει να κάνετε μαθηματικά: το OI έχει αναζητήσει πολλά μέρη για μια σχετικά απλή περιγραφή της κινηματικής που σχετίζεται με αυτόν τον τύπο ρομπότ, αλλά δεν βρήκα ένα που πιστεύω ότι ήταν ένα επίπεδο που οι περισσότεροι άνθρωποι μπορούσαν να το καταλάβουν. Έχω κάνει τη δική μου εκδοχή της κινηματικής βασισμένη αποκλειστικά στην τριγωνομετρία και όχι στους μετασχηματισμούς μήτρας που μπορεί να φαίνονται αρκετά τρομακτικοί αν δεν έχετε δουλέψει ποτέ σε αυτά τα πράγματα - ωστόσο, είναι αρκετά απλοί για το συγκεκριμένο ρομπότ αφού είναι μόνο 3 DOF.

Ωστόσο, νομίζω ότι η προσέγγισή μου στο συνημμένο έγγραφο είναι γραμμένη με σχετικά εύκολο τρόπο κατανόησης. Ρίξτε όμως μια ματιά και δείτε αν έχει νόημα για εσάς!

Βήμα 3: Κωδικοποίηση της Κινηματικής

Η κινηματική μπορεί να είναι δύσκολο να κατανοηθεί ακόμη και με τους υπολογισμούς που παρείχα στο πρώτο. Εδώ είναι πρώτα απ 'όλα μια εφαρμογή Octave - Το Octave είναι ένα δωρεάν εργαλείο με πολλές από τις ίδιες δυνατότητες που βρίσκονται στο Matlab.

L1o = 40; Zo = -70; L_2 = 73,0; Au = 188,0; Al = 182,0; Lo = 47,0; UPPERARMLEN = Au; LOWERARMLEN = Al; XOFFSET = Lo; ZOFFSET = L_2; AZOFFSET = Zo; AXOFFSET = L1o; disp («Υλοποίηση κώδικα») disp («Γωνίες εισαγωγής:») σήψη = deg2rad (30); δεξιά = deg2rad (142,5); αριστερά = deg2rad (50); rad2deg (σήψη) rad2deg (δεξιά) rad2deg (αριστερά) T1 = σήψη;#βάση T2 = δεξιά;#βραχίονας T3 = αριστερά; #elbow #FW κινηματική για να πάρετε το XYZ από γωνίες: disp ('Υπολογίζεται X, Y, Z:') z = ZOFFSET + sin (δεξιά)*LOWERARMLEN - cos (αριστερά - (pi/2 - δεξιά))*UPPERARMLEN + AZOFFSET k1 = αμαρτία (αριστερά - (pi/2 - δεξιά))*UPPERARMLEN + cos (δεξιά)* LOWERARMLEN + XOFFSET + AXOFFSET? x = cos (rot)*k1 y = sin (rot)*k1 ## αντίστροφη κινηματική για να λάβουμε γωνίες από το XYZ: rot = atan2 (y, x); x = x - cos (σήψη)*AXOFFSET; y = y - αμαρτία (σήψη)*AXOFFSET; z = z - AZOFFSET -ZOFFSET; L1 = sqrt (x*x + y*y) - XOFFSET; L2 = sqrt ((L1)*(L1) + (z)*(z)); a = (z)/L2; b = (L2*L2 + LOWERARMLEN*LOWERARMLEN - UPPARARMLEN*UPPERARMLEN)/(2*L2*LOWERARMLEN); c = (LOWERARMLEN*LOWERARMLEN + UPPARARMLEN*UPPARARMLEN - L2*L2)/(2*LOWERARMLEN*UPPERARMLEN); δεξιά = (atan2 (a, sqrt (1-a*a)) + atan2 (sqrt (1-b*b), b)); αριστερά = atan2 (sqrt (1-c*c), c); ## έξοδος υπολογισμένων γωνιών disp ('Γωνίες εξόδου:') σήψη = rad2deg (σήψη) δεξιά = rad2deg (δεξιά) αριστερά = rad2deg (αριστερά)

Με το παραπάνω σενάριο έχετε βασικά τον έτοιμο κώδικα εφαρμογής για κινηματική προς τα εμπρός και προς τα πίσω.

Forward Kinematics που χρησιμοποιείτε για τον υπολογισμό του πού θα καταλήξετε με ένα δεδομένο σύνολο γωνιών κινητήρα. Η αντίστροφη κινηματική θα υπολογίσει (αντίστροφα) ποιες γωνίες κινητήρα χρειάζεστε για να καταλήξετε στην επιθυμητή θέση x, y, z. Στη συνέχεια πρέπει να εισαχθούν περιορισμοί στην κίνηση του κινητήρα, όπως π.χ. η περιστροφική βάση μπορεί να πάει μόνο από 0 έως 359 μοίρες. Με αυτόν τον τρόπο διασφαλίζετε ότι δεν θα πάτε σε θέσεις που δεν είναι εφικτές.

Βήμα 4: Εκτέλεση του Πράγματος

Δεν είμαστε αρκετά εκεί με την εφαρμογή της βιβλιοθήκης κινηματικής, οπότε δεν μπορώ να παράσχω ακόμα. Αλλά μπορώ να σας δείξω ένα βίντεο για το πώς λειτουργεί. Είναι αρκετά σταθερό και ομαλό λόγω της χρήσης ρουλεμάν και ιμάντα, εκτός από την λογική ποιότητα των κινήσεων που είναι εδώ οι πλακέτες uStepper S.

Βήμα 5: Πρόσθετα τελικά εφέ

Έχω σχεδιάσει 3 επιπλέον τελικούς τελεστές. Το ένα είναι απλά μια οριζόντια λαβή, ένα άλλο ταιριάζει με ένα κανονικό ευρωπαϊκό κουτάκι μπύρας ή σόδας και, τέλος, υπάρχει ένα σύστημα λαβής κενού που σας επιτρέπει να τοποθετήσετε σε ένα κύπελλο, αντλία και βαλβίδα κενού.

Όλα θα είναι ή είναι διαθέσιμα εδώ (αρχεία και οδηγίες 3D STL):