
Πίνακας περιεχομένων:
- Βήμα 1: Κατανόηση του αλγορίθμου Μέρος 1: Το οριστικό ολοκλήρωμα και η χρήση του
- Βήμα 2: Κατανόηση του αλγορίθμου Μέρος 2: Αριθμητική προσέγγιση
- Βήμα 3: Κατανόηση του αλγορίθμου Μέρος 3: Ο κανόνας του μεσαίου σημείου
- Βήμα 4: Δημιουργία προγράμματος Μέρος 1: Λήψη μεταγλωττιστή/επεξεργαστή Python
- Βήμα 5: Δημιουργία του προγράμματος Μέρος 2: Εισαγωγή συναρτήσεων και καθορισμός μεταβλητών
- Βήμα 6: Δημιουργία προγράμματος Μέρος 3: Δημιουργία συνάρτησης για ενσωμάτωση
- Βήμα 7: Δημιουργία προγράμματος Μέρος 4: Εμφάνιση της απάντησης
- Βήμα 8: Εκτέλεση του προγράμματος Μέρος 1: Εκτέλεση του προγράμματος ως έχει
- Βήμα 9: Εκτέλεση του προγράμματος Μέρος 2: Ενσωμάτωση άλλων μαθηματικών συναρτήσεων
- Βήμα 10: Εκτέλεση του προγράμματος Μέρος 3: Επέκταση του προγράμματος
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:37.
- Τελευταία τροποποίηση 2025-01-23 14:39.

Αυτό είναι ένα σεμινάριο για το πώς να δημιουργήσετε και να εκτελέσετε ένα πρόγραμμα που θα αξιολογεί ορισμένα ολοκληρωμένα χρησιμοποιώντας έναν αλγόριθμο αριθμητικής ολοκλήρωσης. Χώρισα τα βήματα σε 3 ενότητες: κατανόηση του αλγορίθμου που θα χρησιμοποιηθεί για την κατασκευή του προγράμματος, κωδικοποίηση του προγράμματος χρησιμοποιώντας τη γλώσσα προγραμματισμού Python και εκτέλεση του προγράμματος. Αυτό το σεμινάριο προορίζεται για κάποιον που μπορεί να χρειαστεί να φτιάξει γρήγορα μια αριθμομηχανή για να αξιολογήσει ορισμένα ολοκληρωμένα ή ίσως χρειάζεται τον αλγόριθμο για χρήση σε ένα πρόγραμμα μεγαλύτερης κλίμακας. Αναμένεται βασική γνώση λογισμού, αλλά εξετάζονται οι σχετικές μαθηματικές πληροφορίες. Η γνώση προγραμματισμού δεν είναι αναμενόμενη, αλλά είναι χρήσιμη, καθώς περιγράφω μόνο εν συντομία πώς λειτουργεί πραγματικά ο προγραμματισμός.
Τι θα χρειαστείτε:
Ένας προσωπικός υπολογιστής με πρόσβαση στο διαδίκτυο
Βήμα 1: Κατανόηση του αλγορίθμου Μέρος 1: Το οριστικό ολοκλήρωμα και η χρήση του

Υποθέτω ότι γνωρίζετε λίγο τι είναι ένα ολοκληρωτικό στο πλαίσιο του βασικού λογισμού. Τα ακέραια είναι σημαντικά επειδή σας επιτρέπουν να αθροίσετε έναν πίνακα τιμών πολλαπλασιασμένο με ένα απειροελάχιστο μήκος. αυτό είναι χρήσιμο σε πολλούς τομείς της χρηματοδότησης, της θεωρίας αριθμών, της φυσικής, της χημείας, καθώς και σε πολλούς άλλους τομείς. Αυτό το πρόγραμμα, ωστόσο, θα σας επιτρέψει να υπολογίσετε μόνο την περιοχή κάτω από μια καμπύλη για ένα πεπερασμένο διάστημα, ή με άλλα λόγια, δεν αξιολογεί τα παράγωγα-ένας πολύ ισχυρότερος αλγόριθμος είναι απαραίτητος για αυτό. Αυτός ο αλγόριθμος είναι χρήσιμος εάν πρέπει να αξιολογήσετε ένα οριστικό ολοκλήρωμα σε ένα μεγαλύτερο πρόγραμμα που καθορίζεται για κάτι άλλο ή αν θέλετε να ελέγξετε την απάντησή σας για τυχόν οριστικά ολοκληρωμένα που γίνονται με το χέρι.
Ένα βασικό οριστικό ολοκλήρωμα αντιπροσωπεύει την περιοχή κάτω από μια καμπύλη που ορίζεται από μια συνάρτηση π.χ. f (x) Για ένα οριστικό ολοκλήρωμα, αναζητούμε την περιοχή μεταξύ δύο σημείων (με ετικέτα α και β αντίστοιχα). Στην εικόνα, η τιρκουάζ περιοχή είναι η περιοχή στην οποία αναφέρομαι και η εξίσωση για τον προσδιορισμό αυτού φαίνεται επίσης σε αυτήν την περιοχή. Η λειτουργία που εμφανίζεται στην εικόνα είναι αυθαίρετη.
Βήμα 2: Κατανόηση του αλγορίθμου Μέρος 2: Αριθμητική προσέγγιση

Ένας υπολογιστής χρειάζεται ένα ευρύ σύνολο οδηγιών για τον υπολογισμό αυτής της περιοχής κάτω από μια αυθαίρετη συνάρτηση που θα λειτουργήσει για οποιαδήποτε συνάρτηση, οπότε οι αναλυτικές μέθοδοι που ίσως γνωρίζετε δεν έχουν καμία χρησιμότητα, επειδή είναι πολύ ιδιαίτερες. Μια μέθοδος για τον υπολογισμό των ολοκληρωμάτων περίπου, που ένας υπολογιστής μπορεί πραγματικά να χειριστεί, γίνεται συμπληρώνοντας την περιοχή ενδιαφέροντος με ένα καθορισμένο από τον χρήστη ορθογώνιο ίσου πλάτους και μεταβλητού ύψους και αθροίζοντας όλα τα εμβαδά του ορθογωνίου. Οι άκαμπτες ιδιότητες των ορθογωνίων θα αφήσουν ένα μέρος της συνολικής επιφάνειας ανέγγιχτο, επομένως γιατί αυτό θεωρείται ως προσέγγιση. Ωστόσο, όσο περισσότερα ορθογώνια μπορείτε να στριμώξετε μεταξύ των ορίων (a και b), τόσο πιο ακριβής θα είναι η προσέγγιση, αφού οι άθικτες περιοχές γίνονται πιο αραιές. Δεδομένου ότι ένας υπολογιστής θα εκτελέσει την εργασία, μπορείτε να ορίσετε τον αριθμό των ορθογωνίων στην επιθυμητή περιοχή να είναι πολύ μεγάλος, καθιστώντας την προσέγγιση εξαιρετικά ακριβή. Στην υποστηρικτική εικόνα, φανταστείτε ότι κάθε ορθογώνιο στην καθορισμένη περιοχή έχει ίσο πλάτος. Έκανα ό, τι μπορούσα για να γίνουν ίσο πλάτος στο Microsoft Paint, αλλά δεν έκανα την καλύτερη δουλειά.
Βήμα 3: Κατανόηση του αλγορίθμου Μέρος 3: Ο κανόνας του μεσαίου σημείου

Αυτός ο κανόνας καθορίζει τον τρόπο με τον οποίο τα ορθογώνια γίνονται και χρησιμοποιούνται στην προσέγγιση. Κάθε ορθογώνιο από τα "N" ορθογώνια πρέπει να έχει ίσο πλάτος, Δx, αλλά κάθε nth ορθογώνιο δεν μπορεί να είναι ακριβώς το ίδιο: ο μεταβαλλόμενος συντελεστής είναι το ύψος που ποικίλλει καθώς η συνάρτηση αξιολογείται σε ένα συγκεκριμένο σημείο. Ο κανόνας του μεσαίου σημείου παίρνει το όνομά του από το γεγονός ότι αξιολογείτε το ύψος κάθε ορθογωνίου ως f (x_n), όπου "x_n" είναι το αντίστοιχο κεντρικό σημείο κάθε ορθογωνίου, όπως φαίνεται αριστερά ή δεξιά του ορθογωνίου. Η χρήση του μεσαίου σημείου είναι σαν την εφαρμογή ενός μέσου όρου που θα κάνει την προσέγγιση πιο ακριβή από ό, τι αν χρησιμοποιούσατε το δεξί ή το αριστερό. Η υποστηρικτική εικόνα για αυτό το βήμα συνοψίζει πώς ο κανόνας του μέσου σημείου ορίζεται μαθηματικά.
Βήμα 4: Δημιουργία προγράμματος Μέρος 1: Λήψη μεταγλωττιστή/επεξεργαστή Python
Τώρα που καταλαβαίνετε τον αλγόριθμο που πρέπει να εφαρμοστεί, είναι θέμα να κάνετε έναν υπολογιστή να εκτελέσει τον υπολογισμό για εσάς. Το πρώτο βήμα για να πείτε στον υπολογιστή τι να κάνει είναι να βρείτε τα εργαλεία για να το κάνετε. Αυτός ο αλγόριθμος μπορεί να κωδικοποιηθεί σε οποιαδήποτε γλώσσα. για λόγους απλότητας, αυτό το πρόγραμμα θα κωδικοποιηθεί στη γλώσσα Python. Για να δώσετε εντολή στον υπολογιστή σας να εκτελέσει λειτουργίες με την Python, θα χρειαστείτε έναν επεξεργαστή που θα λαμβάνει οδηγίες γραμμένες σε αυτήν τη γλώσσα, οι οποίες στη συνέχεια θα μεταγλωττιστούν σε γλώσσα μηχανής που μπορεί να καταλάβει ο υπολογιστής σας, ώστε να μπορεί να εκτελέσει τις εργασίες που του λέτε να κάνει. Στην εποχή μας, ένας συντάκτης και ένας μεταγλωττιστής είναι συνήθως ενσωματωμένοι, ωστόσο αυτό δεν συμβαίνει πάντα. Μπορείτε να χρησιμοποιήσετε οποιοδήποτε πρόγραμμα επεξεργασίας/μεταγλωττιστή που σας βολεύει, αλλά θα σας δείξω πώς να αποκτήσετε το προσωπικό μου αγαπημένο για Python: Canopy. Εάν έχετε ήδη έναν επεξεργαστή/μεταγλωττιστή, μπορείτε να παραλείψετε αυτά τα βήματα.
- Μεταβείτε στη διεύθυνση
- Κάντε κλικ στην επιλογή Λήψη θόλου
-
Κάντε κλικ στο κουμπί λήψης που αντιστοιχεί στο λειτουργικό σας σύστημα
Η λήψη θα ξεκινήσει αυτόματα
- Ακολουθήστε τις οδηγίες ενστάλαξης μετά την εκκίνηση του αρχείου εκτέλεσης
- Εκτελέστε το Πρόγραμμα
- Κάντε κλικ στο "Editor" από το κύριο μενού του προγράμματος
- Κάντε κλικ στην επιλογή "δημιουργία νέου αρχείου" στο κέντρο της οθόνης
Από αυτό το σημείο θα πρέπει να δείτε ένα κενό λευκό παράθυρο με έναν δρομέα που μοιάζει με ένα βασικό έγγραφο επεξεργασίας κειμένου. Είστε τώρα έτοιμοι να ξεκινήσετε την κωδικοποίηση του αλγορίθμου αριθμητικής ολοκλήρωσης για την επίλυση ορισμένων ολοκληρωμένων. Τα βήματα που ακολουθούν θα έχουν ένα απόσπασμα κώδικα που θα αντιγράψετε και μια εξήγηση για το τι κάνει αυτό το απόσπασμα για το πρόγραμμα στο σύνολό του.
Βήμα 5: Δημιουργία του προγράμματος Μέρος 2: Εισαγωγή συναρτήσεων και καθορισμός μεταβλητών

Αντιγράψτε τον κώδικα στην εικόνα.
Για οποιοδήποτε πρόγραμμα ενδέχεται να κωδικοποιήσετε, θα υπάρχουν μεταβλητές. Μια μεταβλητή είναι ένα όνομα που δίνεται σε μια τιμή που θα λειτουργήσει και η οποία μπορεί να αλλάξει. Στις περισσότερες γλώσσες προγραμματισμού (αν όχι όλες) πρέπει να προετοιμάσετε μια μεταβλητή προτού το πρόγραμμα μπορεί να κάνει αλλαγές σε αυτήν. Στην περίπτωση αυτού του προγράμματος έχω ονομάσει τις μεταβλητές "N", "a" και "b". Αυτές οι τιμές αντιπροσωπεύουν τον αριθμό των επαναλήψεων (αριθμός ΑΚΑ ορθογωνίων), το κάτω όριο και το ανώτερο όριο αντίστοιχα. Μπορείτε να ονομάσετε ό, τι θέλετε, αλλά για να ταιριάζουν με τους τύπους που δίνονται στην ενότητα "Κατανόηση του αλγορίθμου Μέρος 3: Ο κανόνας του μέσου σημείου", είναι καλύτερο να διατηρούνται οι ίδιοι. Παρατηρήστε ότι δεν έχουν οριστεί μόνο σε μια συγκεκριμένη τιμή. Αυτό συμβαίνει επειδή γίνονται εισόδους που, όταν τρέχει το πρόγραμμα, ο χρήστης του προγράμματος μπορεί να ορίσει ποια θα είναι η τιμή. Το κείμενο σε εισαγωγικά, μετά την εντολή εισαγωγής, εμφανίζεται όταν εκτελείτε το πρόγραμμα και σας ενημερώνει τι είδους τιμή πρέπει να πληκτρολογήσετε. Θα παρατηρήσετε επίσης ότι τα "int" και "float" χρησιμοποιούνται πριν από τους προσδιορισμούς εισόδου. Αυτοί οι όροι λένε στον υπολογιστή τι τύπο μεταβλητής θα είναι αυτή η τιμή. Ένα "int" είναι ένας ακέραιος αριθμός και ένα "float" είναι μια τιμή κυμαινόμενου σημείου (δηλαδή δεκαδικό). Θα πρέπει να είναι σαφές γιατί ορίζονται ως τέτοια.
Κάθε κείμενο που υπάρχει μετά από ένα "#" είναι ένα σχόλιο που επιτρέπει στον προγραμματιστή να ακολουθήσει τον κώδικα με ανθρωπιστικό τρόπο. Έχω κάνει ορισμένα σχόλια στον κωδικό μου τα οποία θα αντιγράψετε, αλλά μη διστάσετε να προσθέσετε τυχόν σχόλια που σας βοηθούν συγκεκριμένα. Το πρόγραμμα δεν θα διαβάσει τίποτα με ένα "#" πριν από αυτό ως εντολή.
Το τμήμα του κώδικα που διαβάζεται "από εισαγωγή μαθηματικών *" λέει στο πρόγραμμα να εισαγάγει μια σειρά μαθηματικών συναρτήσεων που μπορούν να χρησιμοποιηθούν χωρίς να χρειάζεται να τις προγραμματίσετε στον εαυτό σας. Το "*" σημαίνει απλά "όλα". Διαβάστε αυτό το τμήμα του κώδικα ως: από τη βιβλιοθήκη μαθηματικών εισαγάγετε όλες τις συναρτήσεις. Αυτό σας επιτρέπει να χρησιμοποιείτε μαθηματικές συναρτήσεις όπως ημίτονο, συνημίτονο, log, exp, κ.λπ. Αυτές οι συναρτήσεις μπορούν να ενσωματωθούν μαθηματικά στον κώδικα.
Βήμα 6: Δημιουργία προγράμματος Μέρος 3: Δημιουργία συνάρτησης για ενσωμάτωση

Αντιγράψτε τον κωδικό στην εικόνα κάτω από τον προηγούμενο κώδικα.
ΠΡΟΕΙΔΟΠΟΙΗΣΗ: Αυτή η ενότητα είναι πυκνή και θέλω να ξεκαθαρίσω κάποια πράγματα που θα μπορούσαν να προκαλέσουν σύγχυση. Όταν μιλάμε για προγραμματισμό, η λέξη "λειτουργία" εμφανίζεται πολύ. Αυτός ο όρος εμφανίζεται επίσης πολύ όταν μιλάτε για μαθηματικά. Έτσι, από αυτό το σημείο και μετά, όταν μιλάω για μια συνάρτηση με την έννοια του προγραμματισμού, θα γράψω "συνάρτηση Python" και όταν μιλάω για τη μαθηματική συνάρτηση, θα πω "μαθηματική συνάρτηση". Κάποια στιγμή θα χρησιμοποιήσουμε μια συνάρτηση Python ως αναπαράσταση της εν λόγω μαθηματικής συνάρτησης.
Αυτό το επόμενο απόσπασμα κώδικα είναι η καρδιά του προγράμματος. Εδώ, ορίζεται μια συνάρτηση Python που πραγματοποιεί τον αλγόριθμο της αριθμητικής ολοκλήρωσης χρησιμοποιώντας τον κανόνα του μέσου σημείου. "def Integrate (N, a, b)" διαβάζεται ως: ορίστε μια συνάρτηση που ονομάζεται "Integrate" που δέχεται τις μεταβλητές "N", "a" και "b" και επιστρέφει την περιοχή κάτω από την καμπύλη (η μαθηματική συνάρτηση) η οποία ορίζεται επίσης μέσα στη συνάρτηση "Ενσωμάτωση" Python. Μπορείτε να ονομάσετε αυτήν τη συνάρτηση Python οτιδήποτε όταν κάνετε την κωδικοποίηση, αλλά είναι λογικό να την ονομάσετε ενσωμάτωση, καθώς είναι μια συνάρτηση που ενσωματώνει πράγματι μια μαθηματική συνάρτηση.
Σε αυτό το σημείο αξίζει να σχολιάσουμε πώς ο Python διαχωρίζει μπλοκ κώδικα. Ένα μπλοκ κώδικα είναι μια ολόκληρη ενότητα που εκτελεί μια συγκεκριμένη εργασία. Διαφορετικές γλώσσες προγραμματισμού θα έχουν καθορίσει τρόπους διάκρισης αυτών των "μπλοκ". Για την Python, ένα μπλοκ διακρίνεται από εσοχές: κάθε τμήμα που εκτελεί εργασίες έχει τη δική της εσοχή και μπορεί να υπάρχουν μπλοκ εσοχής σε άλλα μπλοκ εσοχής. Αυτό αντιπροσωπεύει εργασίες εντός εργασιών και ουσιαστικά λέει τη σειρά με την οποία πρέπει να εκτελεστεί ο κώδικας. Στην περίπτωση της καθορισμένης συνάρτησης Python "Ενσωμάτωση", όλα μέσα σε αυτήν τη λειτουργία είναι τοποθετημένα σε ένα μπλοκ, διακρίνοντας έτσι τις εργασίες που θα εκτελεστούν σε αυτήν τη συνάρτηση. Υπάρχουν εσοχές σε αυτήν τη λειτουργία Python που εκτελούν επίσης τις δικές τους εργασίες. Έχει ως εξής: ορίζεται μια εντολή (εργασία), μια άνω και κάτω τελεία ακολουθεί την εντολή και αυτό που κάνει η εντολή είναι εσοχή από κάτω.
Αμέσως μετά τον ορισμό της συνάρτησης "ενσωμάτωσης" Python, θα ορίσετε μια άλλη συνάρτηση Python που ονομάζεται f (x). Αυτό αντιπροσωπεύει τη μαθηματική συνάρτηση που θα ενσωματωθεί. Για κάθε διαφορετική μαθηματική συνάρτηση που θέλετε να ενσωματώσετε, θα πρέπει να μεταβείτε σε αυτήν τη γραμμή προγράμματος για να την αλλάξετε (σε αντίθεση με τις μεταβλητές που ορίζονται κατά την εκτέλεση του προγράμματος). Κάθε συνάρτηση Python θα έχει τιμή επιστροφής, αυτό επιστρέφει η συνάρτηση όταν της ρίχνετε μια τιμή. Σε αυτήν την περίπτωση, η τιμή που τίθεται είναι "x", και αυτός ο όρος "x" θα πάρει την αξία αυτού που θα ρίξετε ποτέ-είναι μια προσωρινή τιμή.
Στη συνέχεια, ένας βρόχος for-loop λειτουργεί ως το άθροισμα που ορίζεται στους τύπους στην ενότητα "Κατανόηση του αλγορίθμου" αυτού του σεμιναρίου. Αυτή η άθροιση απαιτεί μερικές ακόμη μεταβλητές, μία από τις οποίες θα λειτουργήσει ως τιμή επιστροφής για ολόκληρη τη συνάρτηση "Ενσωμάτωση" Python. Πριν από το βρόχο for, έχω ορίσει αυτές τις μεταβλητές ως "τιμή" και "τιμή2". Ο στόχος του βρόχου for είναι να επαναλαμβάνεται σε μια σειρά τιμών για μια καθορισμένη μεταβλητή, η οποία μπορεί εύκολα να οριστεί μέσα στην εντολή for-loop. σε αυτήν την περίπτωση, αυτή η μεταβλητή είναι "n". Το εύρος για το οποίο συμβαίνει η επανάληψη είναι 1 έως N+1. Θα πρέπει να παρατηρήσετε ότι το άθροισμα που ορίζεται στους προαναφερθέντες τύπους κυμαίνεται μόνο από 1 έως Ν. Το ορίζουμε με αυτόν τον τρόπο επειδή η γλώσσα Python μετρά κάθε επαναλαμβανόμενη τιμή ξεκινώντας από το μηδέν, οπότε πρέπει ουσιαστικά να μετατοπίσουμε το εύρος των τιμών για να ταιριάζει με το επιθυμητό μας εύρος. Στη συνέχεια, ο βρόχος for επιτρέπει το άθροισμα όλων των υψών του ορθογωνίου μαζί και αποθηκεύει αυτήν την τιμή στη μεταβλητή που ονόμασα "τιμή". Αυτό φαίνεται στο κομμάτι κώδικα που εμφανίζεται ως: τιμή += f (a +((n- (1/2))*((b-a)/N))).
Από εκεί, το επόμενο κομμάτι του κώδικα χρησιμοποιεί τη μεταβλητή που ονομάζεται "τιμή2", η οποία στη συνέχεια εκχωρείται ως το άθροισμα όλων των υψών κάθε ορθογωνίου πολλαπλασιασμένο με το τυποποιημένο πλάτος κάθε ορθογωνίου-αυτή είναι η τελική μας απάντηση που θέλουμε εμφανίζεται από το πρόγραμμά μας και είναι επομένως η τιμή επιστροφής της συνάρτησης Python "Ενσωμάτωση".
Βήμα 7: Δημιουργία προγράμματος Μέρος 4: Εμφάνιση της απάντησης

Αντιγράψτε τον κωδικό στην εικόνα κάτω από τον προηγούμενο κώδικα.
Τώρα που η απάντηση μπορεί να ληφθεί μέσω της συνάρτησης "Ενσωμάτωση" Python, θέλουμε να μπορούμε να την εμφανίζουμε. Αυτό είναι απλώς θέμα τοποθέτησης των τιμών που εισήχθησαν από τον χρήστη ("N", "a" και "b") στη λειτουργία "Integrate" Python και εκτύπωσης στην οθόνη. Αυτή η εντολή εμφανίζεται στη γραμμή 21 και είναι ό, τι πρέπει να κάνετε για να ολοκληρώσετε αυτό το βήμα. Ο κώδικας στις γραμμές 19 και 20 είναι ακριβώς εκεί για να "μεγαλώσει" την έξοδο ολόκληρου του προγράμματος. "εκτύπωση (" ………………………. ")" χωρίζει την ενότητα εισαγωγής του προγράμματος από την ενότητα εξόδου και "εκτύπωση (" Εδώ είναι η απάντησή σας: ")" είναι απλώς ένας χαρακτηρισμός που η απάντηση θα να εκτυπωθεί μετά από αυτήν τη γραμμή κειμένου.
Βήμα 8: Εκτέλεση του προγράμματος Μέρος 1: Εκτέλεση του προγράμματος ως έχει

Εάν δεν χρησιμοποιείτε Canopy, τότε πιθανότατα δεν χρειάζεται καν να ακολουθήσετε αυτό το βήμα καθόλου και η εκτέλεση του προγράμματος ενδέχεται να απαιτεί διαφορετικές διαδικασίες. Στο Canopy, προτού μπορέσετε να εκτελέσετε το πρόγραμμα, θα πρέπει να το αποθηκεύσετε. Ο τύπος αρχείου για ένα πρόγραμμα Python είναι ένα αρχείο.py-αποθηκεύεται αυτόματα ως εξής. Επιλέξτε πού θέλετε να αποθηκευτεί το αρχείο και, στη συνέχεια, θα μπορείτε να εκτελέσετε το πρόγραμμα.
Εκτέλεση του προγράμματος:
- Πατήστε το πράσινο κουμπί που μοιάζει με "κουμπί αναπαραγωγής" που βρίσκεται στη γραμμή εργαλείων ακριβώς πάνω από όπου εμφανίζεται το όνομα του αρχείου σας (ανατρέξτε στην εικόνα).
- Στη συνέχεια, το πρόγραμμα θα εκτελεστεί στην κάτω οθόνη του προγράμματος επεξεργασίας, η οποία είναι γνωστή ως περιβάλλον ανάλυσης δεδομένων Canopy. Υποθέτοντας ότι έχετε αντιγράψει τις προτροπές όπως τις έγραψα, θα πρέπει να δείτε στο κάτω μέρος του περιβάλλοντος ανάλυσης δεδομένων Canopy την προτροπή: "Εισαγάγετε πόσες φορές θέλετε να αθροίσετε (περισσότερες φορές = πιο ακριβείς):." (ανατρέξτε στην εικόνα)
- Εισαγάγετε μια τιμή για το πόσες φορές θέλετε να κάνετε την επανάληψη δηλαδή 10000 (πόσα ορθογώνια θέλετε να σπρώξετε στην περιοχή σας) και μετά πατήστε enter.
- Θα εμφανιστούν περισσότερες προτροπές με προτάσεις που θα πρέπει να είναι οι γνωστές προτροπές εισαγωγής που κωδικοποιήσατε στο πρόγραμμα στο βήμα 5. Συμπληρώστε τις κατάλληλα, όπως στον αριθμό 3 παραπάνω.
- Το ολοκλήρωμα πρέπει να αξιολογηθεί και να εμφανιστεί ένα αποτέλεσμα.
Εάν κωδικοποιήσατε το πρόγραμμα όπως φαίνεται στις προηγούμενες εικόνες, έχετε μόλις ενσωματώσει f (x) = x^2 σε ορισμένα όρια. Το ολοκλήρωμα του x^2 είναι εύκολο να αξιολογηθεί με το χέρι, επομένως θα πρέπει να ελέγξετε και να βεβαιωθείτε ότι το πρόγραμμα έδωσε μια πολύ στενή απάντηση στη σωστή αναλυτική τιμή που καθορίζεται με το χέρι. Όταν τρέχω το πρόγραμμα με τις τιμές N = 10000, a = 0 και b = 10, παίρνω την απάντηση 333.33333249999964. Η σωστή αναλυτική απάντηση, είναι 333.333. Αυτό είναι απίστευτα ακριβές και γρήγορο. Πιέσατε ουσιαστικά 10, 000 ορθογώνια μεταξύ 0 και 10 στον άξονα x και τα χρησιμοποιήσατε για να προσεγγίσετε την περιοχή κάτω από την καμπύλη x^2!
Βήμα 9: Εκτέλεση του προγράμματος Μέρος 2: Ενσωμάτωση άλλων μαθηματικών συναρτήσεων

Στο προηγούμενο βήμα, αν ακολουθήσατε πιστά, ενσωματώσατε f (x) = x^2. Αυτή δεν είναι η μόνη μαθηματική συνάρτηση που μπορεί να ενσωματώσει αυτό το πρόγραμμα. Ανάκληση από το βήμα 5 εισαγάγατε τον πίνακα μαθηματικών βιβλιοθηκών των συναρτήσεων Python στο πρόγραμμα. Αυτό σας επιτρέπει να χρησιμοποιήσετε πιο περίπλοκες μαθηματικές συναρτήσεις που μπορούν να ενσωματωθούν. Ας δώσουμε μια βολή. Φυσικά, μπορείτε να χρησιμοποιήσετε οποιαδήποτε συνάρτηση θέλετε, αλλά θα δείξω περαιτέρω την ακρίβεια αυτού του κώδικα ενσωματώνοντας μια συγκεκριμένη μαθηματική συνάρτηση που αποδίδει μια πολύ γνωστή τιμή όταν ενσωματωθεί σε ένα συγκεκριμένο εύρος. Αυτή η συνάρτηση είναι f (x) = Sin [x]. Αυτή η μαθηματική συνάρτηση εμφανίζεται στην πρώτη συνοδευτική εικόνα, που απεικονίζεται από 0 έως 2π και η περιοχή ενδιαφέροντος σκιάζεται σε τιρκουάζ. Υπάρχει ίση ποσότητα θετικής περιοχής καθώς υπάρχει αρνητική περιοχή σε αυτό το διάστημα, οπότε αν αθροίσετε τη συνολική επιφάνεια, θα πρέπει να πάρετε μηδέν. Ας δούμε αν όντως συμβαίνει αυτό:
Τοποθέτηση της μαθηματικής συνάρτησης f (x) = Sin [x] στο πρόγραμμα:
- Πριν από την εκ νέου εκτέλεση του προγράμματος, κάτω από το σχόλιο "#πληκτρολογήστε τη λειτουργία σας μετά την επιστροφή", πληκτρολογήστε: sin (x) όπου βρίσκεται το x ** 2 αυτήν τη στιγμή. (ανατρέξτε στην εικόνα).
- Εκτελέστε το πρόγραμμα πατώντας ξανά το πράσινο κουμπί αναπαραγωγής.
- Πληκτρολογήστε 10000 για την τιμή Ν (πόσες φορές θέλετε να αθροίσετε).
- βάλτε "0" για το κάτω όριο.
- Βάλτε 6.2832 για το ανώτερο όριο (περίπου 2π).
- Δείτε τι αξία παίρνετε.
Όταν το έκανα αυτό, κατέληξα να παίρνω μια τιμή 1.079e-10: αυτό ισούται με.0000000001079, το οποίο είναι πραγματικά κοντά στο μηδέν, οπότε φαίνεται να είναι ακριβές και δείχνει ότι ο αλγόριθμος χειρίζεται επαρκώς την αρνητική περιοχή.
Βήμα 10: Εκτέλεση του προγράμματος Μέρος 3: Επέκταση του προγράμματος
Σε αυτό το σημείο έχετε τελειώσει: διαθέτετε έναν ολοκληρωμένο ολοκληρωμένο αλγόριθμο κωδικοποιημένο στην Python που λειτουργεί ομαλά και δίνει πολύ ακριβείς απαντήσεις. Ωστόσο, αυτό το πρόγραμμα μπορεί να βελτιωθεί. Δεν είμαι προγραμματιστής και έχω ελάχιστη εμπειρία με την Python. Στην πραγματικότητα, έπρεπε να ανανεωθώ στη χρήση της Python για να ολοκληρώσω αυτό το σεμινάριο, αλλά αυτό θα σας δώσει εμπιστοσύνη ότι η Python είναι τόσο εύκολη στην εκμάθηση γλώσσας. Η άποψή μου είναι ότι μπορείτε να επεκτείνετε αυτό το πρόγραμμα καθιστώντας το πιο αποτελεσματικό, ίσως να εφαρμόσετε κάποιο GUI και να το κάνετε πιο φιλικό προς το χρήστη.
Οι σκέψεις μου για την επέκταση του προγράμματος:
- Εφαρμόστε μια γραφική διεπαφή χρήστη που σας επιτρέπει να εκτελείτε το πρόγραμμα χωρίς να χρησιμοποιείτε το διαδραστικό περιβάλλον ανάλυσης δεδομένων Canopy
- Κάντε το έτσι ώστε η μαθηματική συνάρτηση που πρόκειται να ενσωματωθεί δεν χρειάζεται να εισάγεται μέσα στο πρόγραμμα, αλλά μπορεί να εισαχθεί μετά την εκτέλεση του προγράμματος (αρχικά προσπαθούσα να το κάνω αυτό, αλλά δεν μπορούσα να το καταλάβω).
- Ορίστε μια συνάρτηση Python "Ενσωμάτωση" έτσι ώστε να λάβει τη συνάρτηση f (x) όπως έχει οριστεί για να έχει τη συνάρτηση f (x) καθορισμένη σε αυτήν.
Αυτά είναι μόνο μερικά παραδείγματα τομέων βελτίωσης, αλλά εγγυώμαι ότι υπάρχουν πολλοί άλλοι τομείς που μπορούν να ενισχυθούν. Αφήνω λοιπόν αυτό το βήμα ως παράδειγμα των ελαττωμάτων που έχει αυτό το πρόγραμμα και ίσως μια άσκηση σε όποιον θέλει να βελτιώσει περαιτέρω το πρόγραμμα.
Συνιστάται:
Πώς να φτιάξετε ένα πρόγραμμα οδήγησης υψηλής τάσης για ένα βηματικό μοτέρ: 5 βήματα

Πώς να φτιάξετε ένα πρόγραμμα οδήγησης υψηλής τάσης για ένα βηματικό μοτέρ: εδώ θα δούμε πώς να φτιάξετε ένα πρόγραμμα οδήγησης βηματικού κινητήρα χρησιμοποιώντας τον ελεγκτή TB6560AHQ της Toshiba. Αυτός είναι ένας πλήρης ελεγκτής που χρειάζεται μόνο 2 μεταβλητές ως είσοδο και κάνει όλη τη δουλειά. Αφού χρειάστηκα δύο από αυτά, τα έκανα και τα δύο χρησιμοποιώντας το
Πώς να δημιουργήσετε ένα απλό πρόγραμμα συνομιλίας στη Visual Basic χρησιμοποιώντας το Microsoft Winsock Control: 7 βήματα
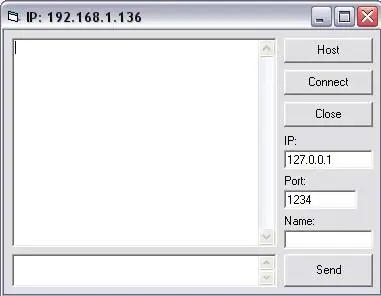
Πώς να φτιάξετε ένα απλό πρόγραμμα συνομιλίας στη Visual Basic χρησιμοποιώντας το Microsoft Winsock Control: Σε αυτό το instuctable θα σας δείξω πώς να κάνετε ένα απλό πρόγραμμα συνομιλίας στο visual Basic. Θα εξετάσω τι κάνει όλος ο κώδικας, έτσι θα μάθετε καθώς τον φτιάχνετε και στο τέλος θα σας δείξω πώς να τον χρησιμοποιήσετε
Πώς να δημιουργήσετε ένα κινούμενο GIF από ένα αρχείο βίντεο χρησιμοποιώντας μόνο δωρεάν λογισμικό: 4 βήματα
Πώς να φτιάξετε ένα κινούμενο GIF από ένα αρχείο βίντεο χρησιμοποιώντας μόνο δωρεάν λογισμικό: για όσους από εσάς δεν γνωρίζετε ένα GIF είναι η πιο συχνά χρησιμοποιούμενη μορφή εικόνας που υποστηρίζει πολλαπλά καρέ σε μια παρουσίαση παρουσίασης ή κινούμενη εικόνα. Με άλλα λόγια, μπορείτε να βάλετε σύντομα βίντεο όπου συνήθως πηγαίνουν μόνο εικόνες. Wantedθελα να κάνω ένα GIF από βίντεο κλιπ
Πώς να δημιουργήσετε ένα πρόγραμμα αναπαραγωγής βίντεο Adobe Flash: 8 βήματα
Πώς να δημιουργήσετε ένα Adobe Flash Video Player: Μόλις επιστρέψατε από τις διακοπές και έχετε πολλά βίντεο για κοινή χρήση. Δημιουργήστε το δικό σας προσαρμοσμένο πρόγραμμα αναπαραγωγής βίντεο για να επιδείξετε αυτές τις αναμνήσεις στο διαδίκτυο. Θα χρειαστείτε έναν υπολογιστή με πρόσβαση στο Διαδίκτυο Αρχείο βίντεο Adobe Flash CS4A
Πώς να δημιουργήσετε ελεύθερα ένα πρόγραμμα οδήγησης κινητήρα L293D: 8 βήματα

Πώς να διαμορφώσετε ελεύθερα έναν οδηγό κινητήρα L293D: Πρόσφατα έκανα ένα έργο που περιελάμβανε βηματικούς κινητήρες και χρειαζόμουν ένα πρόγραμμα οδήγησης κινητήρα που είχε μικρό συντελεστή φόρμας και είχε 4 εξόδους. Αφού τελείωσα και τελειοποίησα την ελεύθερη μορφή μου για αυτό το πρόγραμμα οδήγησης, αποφάσισα να το βάλω εδώ, καθώς φαινόταν ότι δεν ήταν πολλοί άνθρωποι
