Gesture Hawk: Ρομπότ ελεγχόμενης χειρονομίας με χρήση διεπαφής βασισμένη στην επεξεργασία εικόνας: 13 βήματα (με εικόνες)

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:35

Το Gesture Hawk παρουσιάστηκε στο TechEvince 4.0 ως μια απλή διεπαφή ανθρώπου-μηχανής που βασίζεται στην επεξεργασία εικόνας. Η χρησιμότητά του έγκειται στο γεγονός ότι δεν απαιτούνται πρόσθετοι αισθητήρες ή φορετά, εκτός από ένα γάντι για τον έλεγχο του ρομποτικού αυτοκινήτου που λειτουργεί με την αρχή της διαφορικής κίνησης. Σε αυτό το διδακτικό, θα σας καθοδηγήσουμε στην αρχή λειτουργίας πίσω από την παρακολούθηση αντικειμένων και τον εντοπισμό χειρονομιών που χρησιμοποιείται στο σύστημα. Μπορείτε να κατεβάσετε τον πηγαίο κώδικα αυτού του έργου από το Github μέσω συνδέσμου:

Βήμα 1: ΑΠΑΙΤΟΥΜΕΝΑ ΠΡΑΓΜΑΤΑ:

1. L298N Πρόγραμμα οδήγησης κινητήρα
2. DC Motors
3. Πλαίσιο ρομπότ αυτοκινήτου
4. Arduino Uno
5. Μπαταρίες LiPo
6. Καλώδιο USB Arduino (μακρύ)
7. Βιβλιοθήκη OpenCV με Python

Βήμα 2: ΑΡΧΗ ΕΡΓΑΣΙΑΣ:

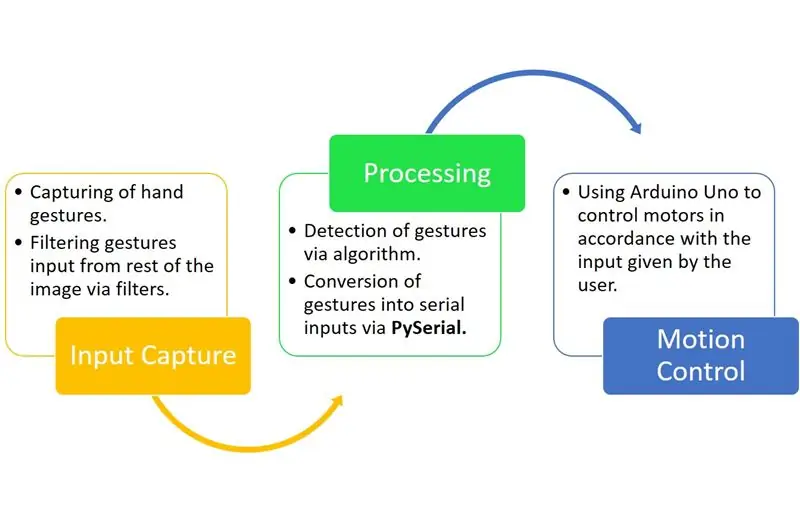
Το Gesture Hawk είναι ένα τριφασικό σύστημα επεξεργασίας όπως μπορείτε να δείτε στο παραπάνω διάγραμμα.

Βήμα 3: ΛΗAPΗ ΚΑΙ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΣΟΔΟΥ:

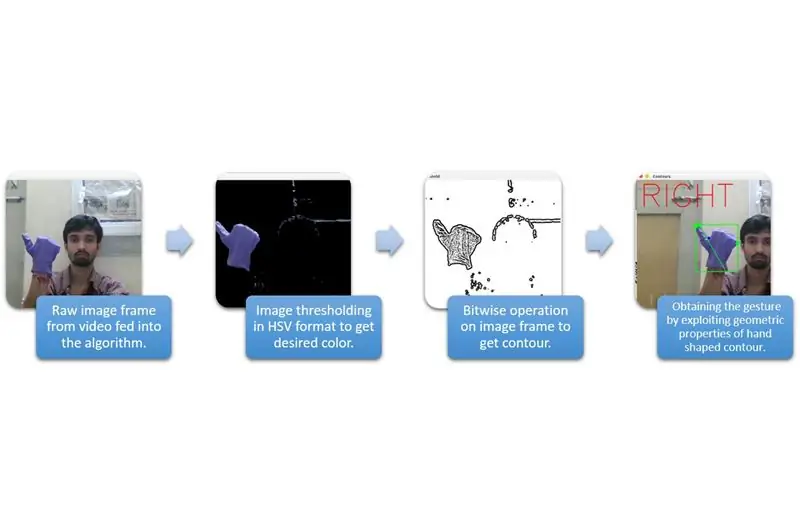
Η καταγραφή εισόδου μπορεί να γίνει κατανοητή στις ευρύτερες κατηγορίες που δίνονται στο παραπάνω διάγραμμα.

Για να εξαγάγουμε το σχήμα του χεριού από το περιβάλλον, πρέπει να χρησιμοποιήσουμε μάσκα ή φιλτράρισμα συγκεκριμένου χρώματος (σε αυτή την περίπτωση - βιολετί μπλε »). Για να το κάνετε αυτό, πρέπει να μετατρέψετε την εικόνα από BGR σε μορφή HSV που μπορεί να γίνει χρησιμοποιώντας το ακόλουθο απόσπασμα κώδικα.

hsv = cv2.cvtColor (πλαίσιο, cv2. COLOR_BGR2HSV)

Τώρα, το επόμενο βήμα είναι να βρείτε το επιθυμητό εύρος παραμέτρων HSV για να εξαγάγετε το χέρι μέσω μάσκας ή φίλτρου. Για αυτό, ο καλύτερος τρόπος είναι να χρησιμοποιήσετε γραμμές παρακολούθησης για την εύρεση κατάλληλου εύρους. Ακολουθεί το στιγμιότυπο οθόνης μιας γραμμής κομματιών που χρησιμοποιείται για αυτό το έργο.

Βήμα 4:

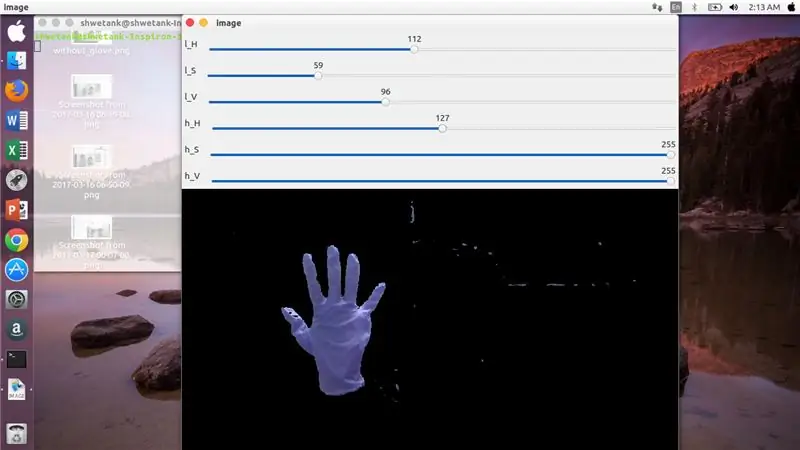
Βήμα 5:

Εδώ, υπάρχει ένα απόσπασμα κώδικα που δίνεται παρακάτω για να δημιουργήσετε μια τέτοια γραμμή παρακολούθησης για κατασκευή μάσκας:

εισαγωγή cv2

εισαγωγή numpy ως npdef τίποτα (x): pass cv2.namedWindow ('image') img = cv2. VideoCapture (0) cv2.createTrackbar ('l_H', 'image', 110, 255, τίποτα) cv2.createTrackbar ('l_S ',' image ', 50, 255, τίποτα) cv2.createTrackbar (' l_V ',' image ', 50, 255, τίποτα) cv2.createTrackbar (' h_H ',' image ', 130, 255, τίποτα) cv2. createTrackbar ('h_S', 'image', 255, 255, τίποτα) cv2.createTrackbar ('h_V', 'image', 255, 255, τίποτα) ενώ (1): _, frame = img.read ()

hsv = cv2.cvtColor (πλαίσιο, cv2. COLOR_BGR2HSV) lH = cv2.getTrackbarPos ('l_H', 'image') lS = cv2.getTrackbarPos ('l_S', 'image') lV = cv2.getTrackbarPos ('l_V', 'εικόνα') hH = cv2.getTrackbarPos ('h_H', 'image') hS = cv2.getTrackbarPos ('h_S', 'image') hV = cv2.getTrackbarPos ('h_V', 'image') lower_R = np πίνακας ([lH, lS, lV]) υψηλότερη_R = np. σειρά ([hH, hS, hV]) μάσκα = cv2.inRange (hsv, lower_R, υψηλότερη_R) res = cv2.bitwise_and (πλαίσιο, πλαίσιο, μάσκα = μάσκα) cv2.imshow ('image', res) k = cv2.waitKey (1) & 0xFF αν k == 27: break cv2.destroyAllWindows ()

Βήμα 6: ΜΕΡΟΣ ΕΠΕΞΕΡΓΑΣΙΑΣ:

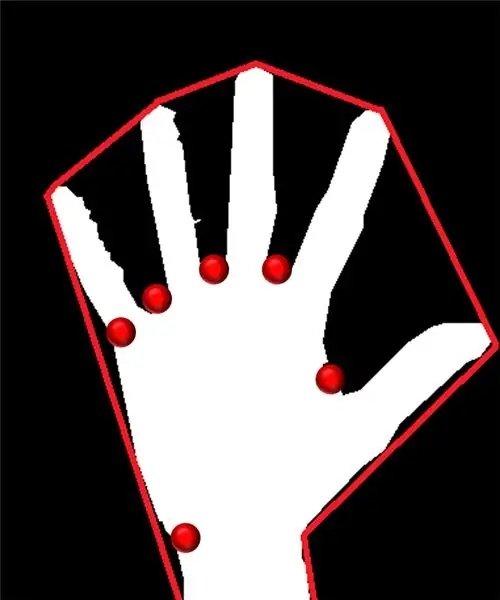
Λοιπόν, έχουμε το γεωμετρικό σχήμα ενός χεριού, τώρα ήρθε η ώρα να το εκμεταλλευτούμε και να το χρησιμοποιήσουμε για να καταλάβουμε τη χειρονομία.

Κυρτό κύτος:

Μέσω κυρτού κύτους, προσπαθούμε να προσαρμόσουμε ένα κατά προσέγγιση πολύγωνο μέσω ακραίων σημείων που υπάρχουν στο σχήμα. Η εικόνα που υπάρχει στα αριστερά δείχνει το κατά προσέγγιση πολύγωνο που είχε αντιστοιχιστεί στο σχήμα με τα κυρτά σημεία να σημειώνονται με κόκκινο.

Τα κυρτά σημεία είναι εκείνα τα σημεία στο σχήμα που βρίσκονται πιο μακριά από μια πλευρά αυτού του κατά προσέγγιση πολυγώνου. Όμως, το πρόβλημα με το κυρτό κύτος είναι ότι κατά τον υπολογισμό του, θα έχουμε μια σειρά από όλα τα κυρτά σημεία, αλλά αυτό που χρειαζόμαστε είναι το μπλε μυτερό κυρτό σημείο. Θα σας πούμε γιατί απαιτείται.

Για να βρούμε αυτό το κυρτό σημείο, πρέπει να εφαρμόσουμε τον κάθετο τύπο απόστασης για να βρούμε την απόσταση του κυρτού σημείου με την πλησιέστερη πλευρά. Παρατηρήσαμε ότι το μπλε αιχμηρό σημείο έχει τη μέγιστη απόσταση από το πλάι και έτσι παίρνουμε αυτό το σημείο.

Βήμα 7:

Βήμα 8:

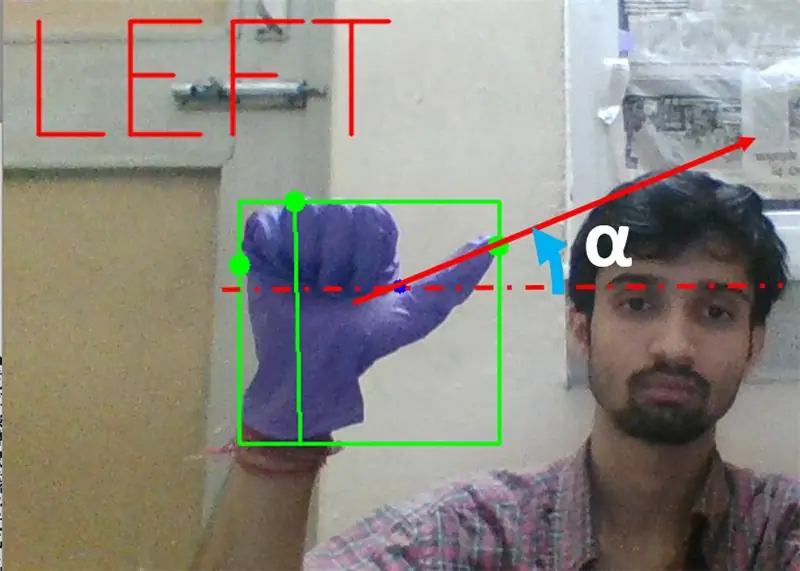
Στη συνέχεια πρέπει να βρούμε την κλίση της γραμμής που ενώνει την άκρη του αντίχειρα (ή το ακραίο σημείο) σε αυτό το κυρτό σημείο με οριζόντιο.

Βήμα 9:

Στην παραπάνω περίπτωση, η γωνία α πρέπει να είναι μεταξύ 0 και 90 μοιρών εάν η κίνηση είναι για αριστερή στροφή. Δηλαδή το μαύρισμα (α) πρέπει να είναι θετικό.

Βήμα 10:

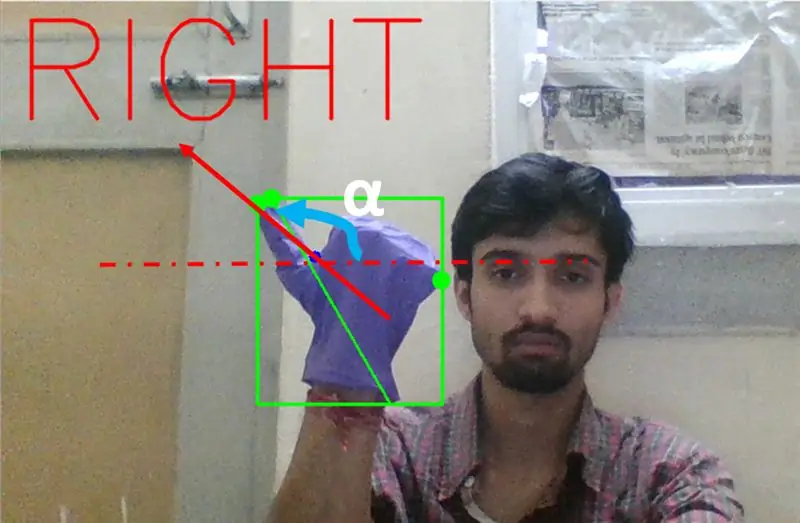
Στην παραπάνω περίπτωση, η γωνία α πρέπει να είναι μεταξύ 180 και 90 μοιρών εάν η κίνηση είναι για δεξιά στροφή. Δηλαδή το μαύρισμα (α) πρέπει να είναι αρνητικό.

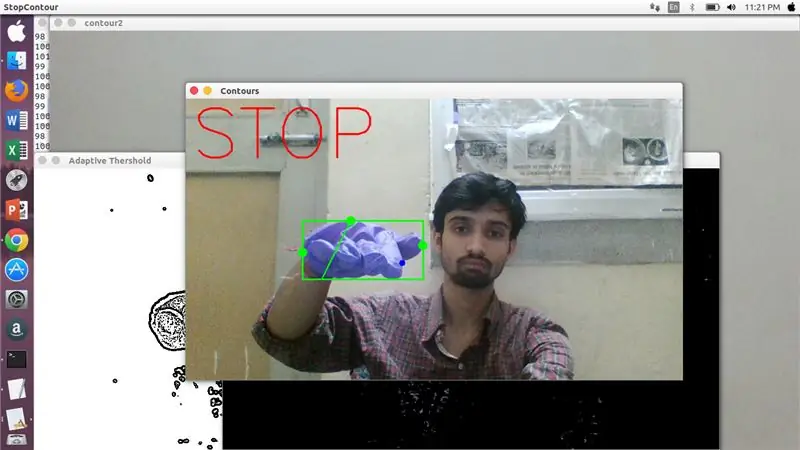
Επομένως, εάν το Tan α είναι θετικό, τότε στρίψτε αριστερά. Εάν το Tan α είναι αρνητικό, τότε στρίψτε δεξιά. Τώρα, ήρθε η ώρα να δούμε πώς να εντοπίσουμε την πιο σημαντική εντολή διακοπής.

Εδώ, εξετάζεται μια καθορισμένη αναλογία (που βρέθηκε με χτύπημα και δοκιμή) και σε μέγιστες περιπτώσεις αυτός ο λόγος αποστάσεων παραμένει σε αυτό το συγκεκριμένο εύρος.

Βήμα 11:

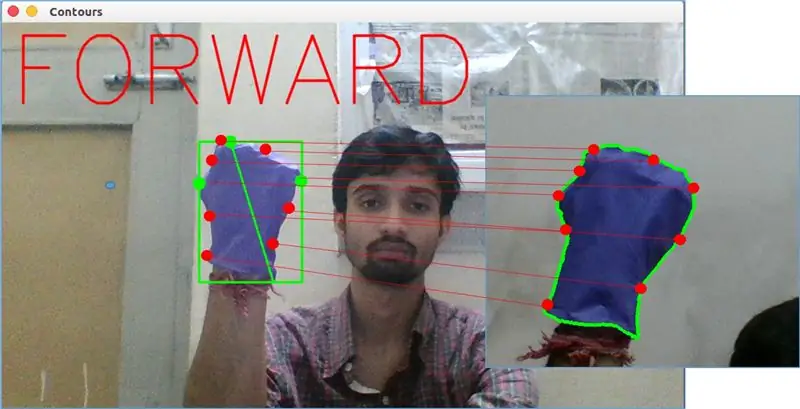
Επιτέλους, η κίνηση προς τα εμπρός αναλύεται με τη λειτουργία matchShape () στο OpenCV. Αυτή η συνάρτηση συγκρίνει το σχήμα δύο μετρητών, σε αυτήν την περίπτωση, μεταξύ του παραδείγματος προπόνησης σε πλήρη εικόνα στην παραπάνω εικόνα με το περίγραμμα στην αριστερή πλευρά της παραπάνω εικόνας. Επιστρέφει μια τιμή που κυμαίνεται από 0 έως 2 ή 3, σύμφωνα με την παραλλαγή που υπάρχει στο σχήμα δύο περιγραμμάτων. Για το ίδιο ίδιο περίγραμμα, επιστρέφει 0.

ret = cv2.matchShapes (cnt1, cnt2, 1, 0.0)

Εδώ, τα cn1 και cnt2 είναι τα δύο περιγράμματα που πρέπει να συγκριθούν.

Βήμα 12: ΕΛΕΓΧΟΣ ΚΙΝΗΣΗΣ:

PySerial:

Χρησιμοποιήσαμε τη βιβλιοθήκη PySerial της python για να μετατρέψουμε τα επεξεργασμένα δεδομένα σε σειριακά δεδομένα για επικοινωνία στο Arduino Uno μέσω καλωδίου USB Arduino. Μόλις εντοπιστεί μια συγκεκριμένη χειρονομία από το opencv, δημιουργήσαμε μια προσωρινή μεταβλητή πείτε ‘x’ και της εκχωρήσαμε κάποια μοναδική τιμή και τη μετατρέψαμε σε σειριακή είσοδο χρησιμοποιώντας την ακόλουθη γραμμή εντολών:-

εισαγωγή σειριακού #για εισαγωγή Pyserial βιβλιοθήκης

σειριακό (Serial)

serial.write (b'x ') # x είναι το αλφάβητο που αποστέλλεται στη θύρα … b είναι η μετατροπή αυτής της συμβολοσειράς σε byte.

Επεξεργασία Arduino:

Τώρα το arduino κωδικοποιείται με τέτοιο τρόπο ώστε κάθε διαφορετικό σειριακό x να χαρτογραφείται γραμμικά σε συγκεκριμένη ενέργεια που είναι υπεύθυνη για την ομαλή κίνηση του ρομπότ (ας πούμε ότι η ανίχνευση της αριστερής χειρονομίας θα ενεργοποιήσει τους κινητήρες στα δεξιά για να στρίψουν αριστερά). Μπορούμε να ελέγξουμε την κίνηση κάθε τροχού μεταφραστικά αλλά και περιστροφικά αλλάζοντας σωστά τον κώδικα.

L298N Πρόγραμμα οδήγησης κινητήρα:-

Το Motor Driver χρησιμοποιείται ως διαμεσολαβητής μεταξύ του κινητήρα και της πηγής ισχύος, καθώς οι κινητήρες δεν μπορούν να τροφοδοτηθούν απευθείας λόγω των χαμηλών τάσεων. Η μπαταρία Li-Po είναι συνδεδεμένη με τον ακροδέκτη εισόδου 12V και συνδέουμε την πρίζα του arduino με την πρίζα εισόδου 5V του οδηγού μοτέρ που συνδέει τελικά τη γείωση του Li-Po καθώς και το arduino σε μια κοινή πρίζα του οδηγού κινητήρα.

Τώρα οι ακροδέκτες των κινητήρων συνδέονται στις πρίζες που δίνονται. Τέλος, συνδέουμε τους ακροδέκτες εισόδου για τον κινητήρα στις υποδοχές εξόδου PWM του arduino, επιτρέποντάς μας να αποφασίσουμε με ακρίβεια τις πλευρές περιστροφής και μετάφρασης της κίνησης.