Πώς να μετρήσετε τον κύκλο υψηλής συχνότητας και λειτουργίας, ταυτόχρονα, χρησιμοποιώντας έναν μικροελεγκτή .: 4 βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:36

Ξέρω τι νομίζετε: "Ε; Υπάρχουν πολλές οδηγίες για τον τρόπο χρήσης μικροελεγκτών για τη μέτρηση της συχνότητας του σήματος. Χασμουρητό." Αλλά περιμένετε, υπάρχει μια καινοτομία σε αυτό: Περιγράφω μια μέθοδο μέτρησης συχνοτήτων πολύ υψηλότερη από ό, τι αντέχει ένας μικροελεγκτής (MCU) και ο κύκλος λειτουργίας του σήματος - όλα ταυτόχρονα!

Το εύρος συχνοτήτων της συσκευής εκτείνεται από ~ 43 Hz έως ~ 450 kHz, ενώ ο κύκλος λειτουργίας κυμαίνεται από 1% έως 99%.

Επιτρέψτε μου να εξηγήσω το μέρος "μπορεί να αντέξει": ένα MCU μετρά την περίοδο ενός σήματος τετραγωνικού κύματος, T, παρακολουθώντας το χρόνο μεταξύ δύο επόμενων συμβάντων μετάβασης. Για παράδειγμα, από χαμηλή προς υψηλή τάση πηδά σε μία από τις ακίδες εισόδου/εξόδου. Το κάνει μετρώντας τον αριθμό των παλμών του εσωτερικού του ρολογιού. Απλώς, το ανώτατο όριο για τις μετρημένες συχνότητες πρέπει να υπακούει στο θεώρημα δειγματοληψίας Nyqvist-Shannon. δηλαδή, θα ισούται περίπου με το ήμισυ της συχνότητας ρολογιού των MCU. Στην πραγματικότητα, το όριο είναι πολύ, πολύ χαμηλότερο, επειδή το MCU πρέπει να εκτελέσει κώδικα για να χειριστεί διακοπές, να αποθηκεύσει μεταβλητές, να κάνει αριθμητικές πράξεις, να εμφανίσει αποτελέσματα κ.λπ. Στα πειράματά μου με MCU 48 MHz ο ελάχιστος αριθμός κύκλων ρολογιού μεταξύ μετρήσιμων μεταβάσεων ήταν περίπου 106. Επομένως, το ανώτερο όριο του μετρήσιμου εύρους συχνοτήτων σε αυτή την περίπτωση θα είναι 48, 000 /212 /2 = 226,4 kHz.

Ενώ το MCU μετρά την περίοδο του σήματος, μπορεί επίσης να καθορίσει το πλάτος του παλμού του, P: ο χρόνος της τάσης του σήματος που παραμένει υψηλός. Με άλλα λόγια, ο χρόνος μεταξύ χαμηλών προς υψηλών και υψηλών προς χαμηλών μεταβάσεων. Ο κύκλος λειτουργίας του σήματος ορίζεται στη συνέχεια ως το ακόλουθο ποσοστό:

Καθήκον = 100% * Ρ / Τ

Ακριβώς όπως στην περίπτωση της συχνότητας, υπάρχει ένα πρακτικό όριο στο πλάτος του παλμού. Χρησιμοποιώντας το παραπάνω παράδειγμα, 106 κύκλοι ρολογιού θα περιορίσουν το πλάτος του παλμού σε λιγότερο από 2,21 μικροδευτερόλεπτα. Or, τουλάχιστον 50% στα 226,4 kHz.

Ένας από τους τρόπους αύξησης του ανώτερου ορίου συχνότητας των σημάτων τετραγωνικών κυμάτων είναι η εφαρμογή ψηφιακών διαιρέσεων που χρησιμοποιούν σαγιονάρες. Ο διαχωρισμός της συχνότητας εισόδου με n θα επέκτεινε το μετρήσιμο ανώτερο εύρος n φορές. Αυτά είναι υπέροχα νέα, οι ψηφιακοί διαχωριστές έχουν ένα θεμελιώδες ελάττωμα: το διαιρεμένο σήμα χάνει τις πληροφορίες πλάτους παλμού (και κύκλου λειτουργίας)! Λόγω του τρόπου με τον οποίο λειτουργούν τα διαχωριστικά, η παραγωγή τους έχει πάντα 50% κύκλο λειτουργίας. Bummer…

Στις επόμενες σελίδες, ωστόσο, θα δείξω πώς να διαιρέσω ψηφιακά τη συχνότητα και να διατηρήσω το αρχικό πλάτος παλμών επιτρέποντάς μου να μετρήσω σήματα πολύ πέρα από τα όρια που επιβάλλονται από την άμεση καταμέτρηση.

Βήμα 1: Διαίρεση ψηφιακών συχνοτήτων

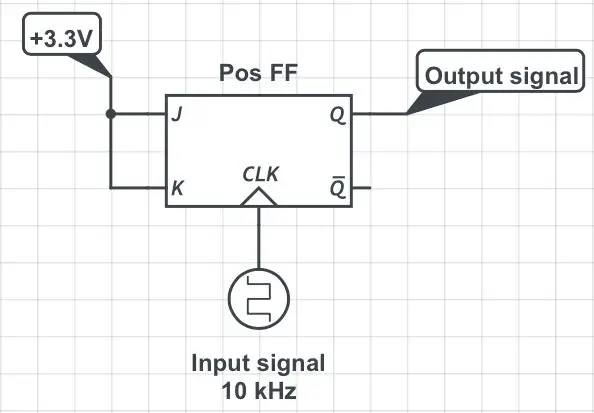
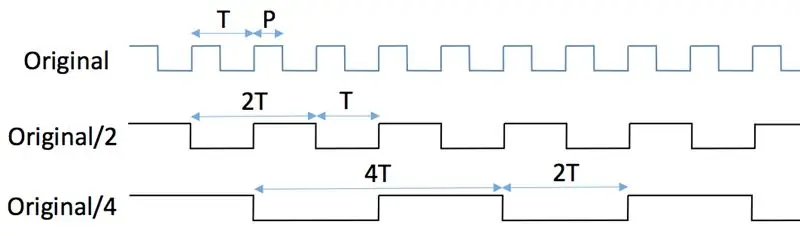
Τα παραδοσιακά ψηφιακά διαχωριστικά συχνοτήτων χρησιμοποιούν σαγιονάρες. αυτό το σεμινάριο εξηγεί όμορφα τις αρχές πώς να κατασκευάσετε διαχωριστικά χρησιμοποιώντας τυπικά σαγιονάρες JK. Αυτό λύνει το πρόβλημα των συχνοτήτων εισόδου πολύ υψηλών για το MCU, αλλά έχει ένα σημαντικό μειονέκτημα: το διαιρεμένο σήμα έχει κύκλο λειτουργίας 50%, ανεξάρτητα από τη λειτουργία του σήματος εισόδου! Για να δείτε γιατί συμβαίνει, κοιτάξτε τις δύο πρώτες φιγούρες. Το αρχικό σήμα με την περίοδο T και το πλάτος του παλμού P τροφοδοτείται στον πείρο ρολογιού μιας σαγιονάρτας JK ενώ οι ακίδες J και K του διατηρούνται ψηλά ανά πάσα στιγμή (πρώτο σχήμα). Η λογική των 3.3V υποτίθεται σε ολόκληρο. Ας υποθέσουμε ότι το flip-flop ενεργοποιείται από τη θετική (δηλαδή, ανερχόμενη) άκρη του ρολογιού. Υπό αυτές τις συνθήκες, αλλαγές της κατάστασης του πείρου εξόδου (μεμονωμένα "flips" και "flops") συμβαίνουν κάθε φορά που ο πείρος του ρολογιού μεταβαίνει από χαμηλά σε υψηλά. Η υψηλή προς τη χαμηλή μετάβαση του ρολογιού (δηλ. Το αρνητικό άκρο) αγνοείται εντελώς. Δείτε το δεύτερο σχήμα. Ο ακροδέκτης εξόδου, Q, εκπέμπει ένα σήμα του οποίου η περίοδος είναι διπλάσια από την αρχική περίοδο, δηλαδή η συχνότητά του μειώνεται στο μισό. Το πλάτος παλμών εξόδου είναι πάντα ίσο με Τ. Κατά συνέπεια, το αρχικό πλάτος παλμού, Ρ, χάνεται.

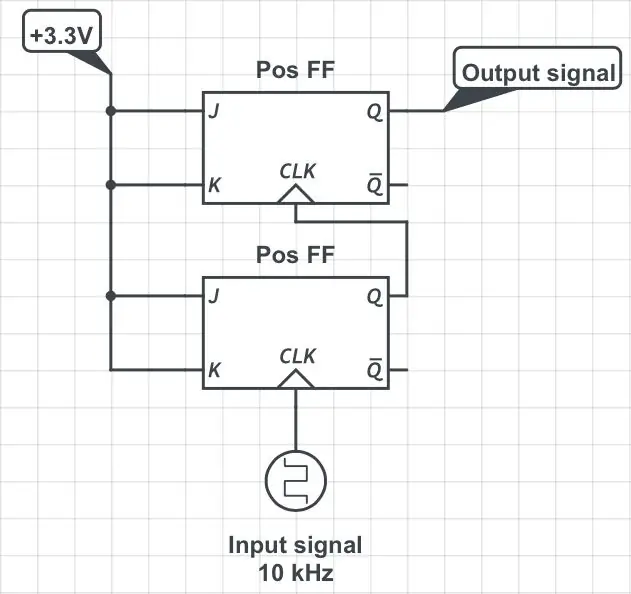
Η προσθήκη ενός άλλου flip-flop JK σε μια διαμόρφωση που φαίνεται στο τρίτο σχήμα διαιρεί την αρχική συχνότητα με 4. Η προσθήκη περισσότερων σαγιονάρων με τον ίδιο διαδοχικό τρόπο διαιρεί τη συχνότητα με τις επόμενες δυνάμεις 2: 8, 16, 32 κ.λπ.

Πρόβλημα: πώς να διαιρέσετε τη συχνότητα ενός τετραγωνικού κύματος διατηρώντας παράλληλα το πλάτος του παλμού;

Η ιδέα είναι να προσθέσετε σωστά μια αρνητική άκρη ενεργοποιημένη JK flip-flop στο μείγμα. Ας το ονομάσουμε "Neg FF". δείτε το τέταρτο σχήμα. Εδώ, "σωστά" σημαίνει ότι οι ακίδες J και K του νέου flip-flop είναι δεμένες με τις ακίδες εξόδου Q και Qbar, αντίστοιχα, του διαχωριστή-προς-4 ("Pos FF") που απεικονίζεται στο προηγούμενο σχήμα. (Εδώ, η "γραμμή" είναι η οριζόντια γραμμή πάνω από το σύμβολο Q που υποδεικνύει τη λογική άρνηση.) Για να δείτε τι επιτυγχάνεται, ρίξτε μια ματιά στον πίνακα λειτουργιών του "Neg FF" στο πέμπτο σχήμα: Οι ακίδες εξόδου του Neg, Q και Qbar, αντικατοπτρίζει την κατάσταση των ακίδων εισόδου του, J και K, αντίστοιχα. Αυτό σημαίνει ότι αντικατοπτρίζουν την κατάσταση του Q και του Qbar του Pos. Όμως, η δράση του Neg's flip-flop πρέπει να περιμένει το αρνητικό άκρο του αρχικού σήματος, το οποίο φτάνει τη στιγμή P μετά το θετικό άκρο. Αχα!

Οι προκύπτουσες κυματομορφές απεικονίζονται στο έκτο σχήμα. Το σήμα εξόδου "Pos Q" εκπέμπει σε 1/4 συχνότητα, το "Pos Qbar" είναι αντίστροφο, το "Neg Q" ακολουθεί το "Pos Q" που μετατοπίζεται κατά το πλάτος του παλμού P και το "Neg Qbar" είναι το αντίστροφο. Μπορείτε να επαληθεύσετε ότι το λογικό ΚΑΙ των "Pos Qbar" και "Neg Q" παράγει μια παλμική αμαξοστοιχία που χαρακτηρίζεται από το αρχικό πλάτος παλμών P και 1/4 της συχνότητας. Λοταρία!

Στην αρχή χρησιμοποίησα ακριβώς αυτό το σήμα εξόδου για να τροφοδοτήσω το MCU. Ωστόσο, αποδείχθηκε ότι ήταν προβληματικό για πολύ μικρά πλάτη παλμών λόγω του περιορισμού των 106 κύκλων του MCU που αναφέρεται στην Εισαγωγή. Έχω λύσει αυτό το μικρό πρόβλημα επιλέγοντας μια άλλη έξοδο: "Pos Qbar" ΚΑΙ "Neg Qbar". Μια ματιά στις κυματομορφές θα σας πείσει ότι το πλάτος παλμών της συγκεκριμένης κυματομορφής, P ', κυμαίνεται μεταξύ T και 2T αντί για το εύρος (0, T) για το P. Το P μπορεί εύκολα να ανακτηθεί από το P' με:

P = 2T - P '

Βήμα 2: Προτεινόμενο υλικό

Μου αρέσει πολύ ο σχετικός νεοεισερχόμενος στους ηλεκτρονικούς χομπίστες: Atmel SAM D21 MCU με βάση τον επεξεργαστή 32-bit ARM Cortex M0+ που λειτουργεί σε ρυθμό ρολογιού 48 MHz, πολύ υψηλότερος από τους παλαιότερους Atmels. Για αυτό το έργο αγόρασα:

• Πλακέτα ItsyBitsy M0 Express MCU από το Adafruit
• Έτυχε να έχω μια επαναφορτιζόμενη μπαταρία LiPo από το Adafruit
• Μονόχρωμη οθόνη OLED 128x32 SPI (το μαντέψατε: Adafruit)
• Διπλό σακίδιο JK με διπλή θετική άκρη SN74HC109 από την Texas Instruments
• Διπλό JK σαγιονάρες SN74HC112 με ενεργοποίηση αρνητικού άκρου από την Texas Instruments
• Τετράκλινο AND gate CD74AC08E από Texas Instruments
• Τετραπλή ή πύλη CD74AC32E από την Texas Instruments

Βήμα 3: Το κύκλωμα

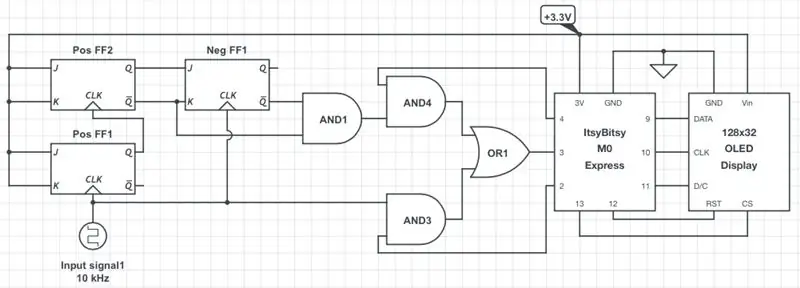
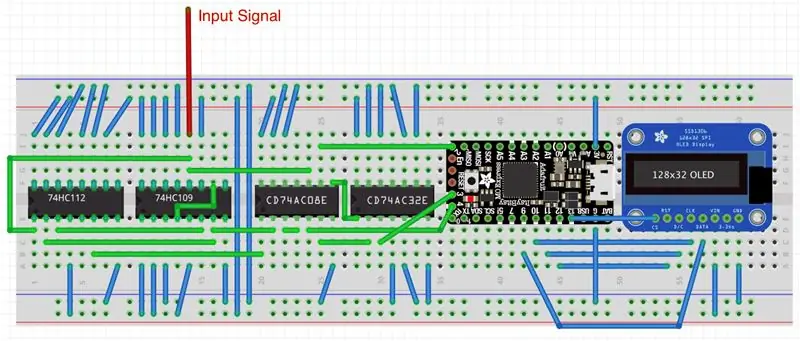
Το πρώτο σχήμα δείχνει ένα απλοποιημένο σχήμα του μετρητή συχνότητας/λειτουργίας. Η λογική CMOS των 3,3 V υποτίθεται σε ολόκληρο. Κατά συνέπεια, το πλάτος του τετραγωνικού κύματος εισόδου πρέπει να είναι μεταξύ του αντίστοιχου V_IH επίπεδο (δηλαδή, 2 V) και 3,3 V. Εάν όχι, πρέπει να το κλιμακώσετε προς τα πάνω ή προς τα κάτω ανάλογα. Στις περισσότερες περιπτώσεις αρκεί ένας απλός διαιρέτης τάσης. Εάν θέλετε να σχεδιάσετε την έκδοση του μετρητή σας σε διαφορετικό λογικό επίπεδο, τότε πρέπει να χρησιμοποιήσετε ένα άλλο μικροελεγκτή (MCU), μπαταρία και μια οθόνη που λειτουργεί στο επιθυμητό επίπεδο. Οι λογικές πύλες και οι σαγιονάρες που χρησιμοποιούνται σε αυτό το έργο λειτουργούν με λογικά επίπεδα οπουδήποτε μεταξύ 2 V και 6 V και θα πρέπει να είναι εντάξει στις περισσότερες περιπτώσεις.

Όπως φαίνεται, το ItsyBitsy MCU χρησιμοποιεί ακίδες 9-13 για επικοινωνία με την οθόνη μέσω του πρωτοκόλλου λογισμικού SPI. Ο πείρος 3V παρέχει ισχύ σε ολόκληρο το κύκλωμα. Ο ακροδέκτης ψηφιακής εισόδου 3 δέχεται το αναλυμένο σήμα, ενώ οι ακίδες 2 και 4 ελέγχουν την πηγή σήματος: είτε άμεσο σήμα που προέρχεται από την πύλη AND3 (χαμηλές συχνότητες εισόδου), είτε σήμα διαιρούμενο με 4 μέσω της πύλης AND4 (υψηλές συχνότητες εισόδου) όπως περιγράφεται στο βήμα 2 Ο κώδικας, που συζητήθηκε στο επόμενο βήμα, ανιχνεύει αυτόματα το εισερχόμενο εύρος συχνοτήτων και αλλάζει κατάλληλα την πηγή σήματος.

Το σχήμα δεν δείχνει την πραγματική πολυπλοκότητα των συνδέσεων ψηφιακών τσιπ. Η δεύτερη εικόνα δείχνει πώς θα φαινόταν το έργο σε μια σανίδα ψωμιού. Το σήμα εισόδου έρχεται μέσω ενός κόκκινου σύρματος στον πείρο 2CLK του διπλού θετικού άκρου flip-flop. ΠΡΟΣΟΧΗ: Κανονικά, όλοι οι ακροδέκτες J και K αυτού του σαγιονάρου πρέπει να είναι ψηλά, αλλά ο SN74HC109 συγκεκριμένα διαθέτει τον πείρο Kbar - έναν ανεστραμμένο πείρο Κ - αντ 'αυτού. Επομένως, αυτός ο πείρος πρέπει να είναι γειωμένος! Το πρώτο flip-flop αρνητικού άκρου στο SN74HC112 έχει τον ακροδέκτη 1K και 1J που συνδέεται με τους ακροδέκτες 1Q και 1Qbar του SN74HC109. Το δεύτερο flip-flop στο SN74HC112 δεν χρησιμοποιείται και οι ακίδες εισόδου του (2K, 2J, 2CLRbar) είναι γειωμένες. Όλες οι άλλες πρόσθετες ακίδες PREbar (προεπιλογή) και CLRbar (διαγραφή) σε όλες τις σαγιονάρες πρέπει να είναι συνδεδεμένες σε λογικό υψηλό. Οι αχρησιμοποίητες ακίδες ρολογιού και εξόδου παραμένουν ασύνδετες. Ομοίως, οι αχρησιμοποίητες ακίδες εισόδου σε όλες τις πύλες είναι γειωμένες, ενώ οι αχρησιμοποίητες ακίδες εξόδου παραμένουν ασύνδετες. Όπως συζήτησα στο «Αόρατος δολοφόνος του δακτυλίου τηλεφώνου» με οδηγίες, η γείωση αχρησιμοποίητων ακίδων εισόδου λογικών τσιπ εξαλείφει τις τυχαίες ταλαντώσεις και εξοικονομεί ενέργεια από την μπαταρία.

Βήμα 4: Ο κώδικας και η μέτρηση χαμηλών συχνοτήτων

Φυσικά, όλη η ενέργεια πραγματοποιείται στον παρακάτω κώδικα. Όταν η είσοδος που εισέρχεται στον ακροδέκτη 3 αλλάζει από ψηφιακό χαμηλό σε υψηλό, το MCU αρχίζει να μετρά τους παλμούς του εσωτερικού του ρολογιού 48 MHz. Σημειώνει τη στιγμή μετάβασης από υψηλή σε χαμηλή και συνεχίζει την καταμέτρηση μέχρι τον επόμενο διακόπτη χαμηλής προς υψηλής, όταν επανεκκινεί ξανά ολόκληρη τη διαδικασία. Η πρώτη καταμέτρηση αντιπροσωπεύει το πλάτος του παλμού, ενώ ολόκληρη η μέτρηση αντιπροσωπεύει την περίοδο του σήματος. Και αυτό είναι όλο το μυστικό.

Η CPU σημειώνει αυτές τις μεταβάσεις μέσω διακοπών υλικού. Το SAMD21 έχει πολλά ρολόγια. ο κωδικός μου χρησιμοποιεί ένα TC3. Αρχικά, ξεκίνησα διαβάζοντας το φύλλο δεδομένων του M0 για πολλή προσπάθεια για την κωδικοποίηση του χειριστή διακοπών, αλλά σύντομα ανακάλυψα έναν πολύ σχετικό κώδικα στις αναρτήσεις του Φόρουμ Arduino από χρήστες electro_95, MartinL και Rucus των οποίων η συμβολή είναι αναγνωρίζεται δεόντως. Ενσωμάτωσα και τροποποίησα τον συνδυασμένο κωδικό τους στον δικό μου. εξοικονομώντας μου πολύ χρόνο!

Όπως ανέφερα προηγουμένως, η ανάλυση σήματος περιορίζεται από cles 106 κύκλους CPU για την εκτέλεση κώδικα μεταξύ διακοπών. Η ψηφιακή διαίρεση με διατήρηση του πλάτους του παλμού φροντίζει για υψηλές συχνότητες. Οι χαμηλές συχνότητες, από την άλλη πλευρά, δημιουργούν μια άλλη πρόκληση: δεδομένου ότι ο μετρητής ρολογιού TC3 έχει μήκος 16 bit, ξεχειλίζει αφού ξεπεράσει το όριο 65, 536 μετρήσεων. Κάποιος μπορεί να χειριστεί αυτήν την κατάσταση προσθέτοντας μια διακοπή υπερχείλισης, αλλά επέλεξε μια διαφορετική λύση: Το TC3 μπορεί να χρησιμοποιήσει ένα ρολόι CPU με προεπιλεγμένη κλίμακα (δηλαδή διαιρεμένη σε λογισμικό) αντί για ένα υλικό 48 MHz. Έτσι, εάν η περίοδος του σήματος πλησιάσει το όριο υπερχείλισης, ο κώδικας μπορεί να δώσει εντολή στο TC3 να χρησιμοποιήσει μετρητές 24 MHz για την επόμενη περίοδο και, voila, ο μετρητής πέσει κάτω από τους 32, 768 μετρήσεις. Για ακόμη χαμηλότερες συχνότητες, το TC3 μπορεί να λάβει εντολή να μετρήσει παλμούς 12 MHz, κλπ. Ο κατάλληλος προδιαγραφέας προσδιορίζεται αυτόματα με βάση τη συχνότητα του σήματος, με υστέρηση, προκειμένου να διατηρείται ο μετρητής TC3 εντός του ορίου υπερχείλισης. Ως αποτέλεσμα, το κάτω άκρο της εμβέλειας της συσκευής είναι περίπου 43 Hz.

Είστε ευπρόσδεκτοι να αλλάξετε τον κωδικό και να τον χρησιμοποιήσετε στο έργο σας, αλλά αναφέρετε την πηγή του κατά τη δημοσίευση αποτελεσμάτων.

Σύνδεσμος προς τον κώδικα.