DIY Laser Steering Module για Arduino: 14 βήματα (με εικόνες)

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:37

Σε αυτό το Instructable, θα δείξω την κατασκευή μιας μονάδας διεύθυνσης δέσμης λέιζερ διπλού άξονα, μονής καθρέφτη, χρησιμοποιώντας τρισδιάστατα τυπωμένα μέρη και φθηνά εξαρτήματα από το eBay.

Αυτό το έργο έχει ομοιότητες με το Arduino Laser Show με το Full XY Control και το Arduino Laser Show With Real Galvos, αλλά πιστεύω ότι είναι το πρώτο που χρησιμοποίησε 3D εκτυπωμένο σχέδιο με φθηνά σωληνοειδή. Βάζω όλα τα αρχεία σχεδίασης κάτω από το GPLv3, έτσι ώστε ο σχεδιασμός να μπορεί να βελτιωθεί και να βελτιωθεί.

Αν και προς το παρόν έχω συγκεντρώσει μόνο τη μονάδα και έχω γράψει έναν πολύ βασικό κωδικό δοκιμής, η ελπίδα μου είναι ότι μια μέρα θα μπορέσω να τον ανεβάσω στο επόμενο επίπεδο ενσωματώνοντας τον κώδικα διανυσματικών γραφικών από το προηγούμενο Instructable, Super Fast Analog Voltages από το Arduino.

Βήμα 1: Συγκεντρώστε τα μέρη που δεν εκτυπώνονται σε 3D

Το συγκρότημα λέιζερ αποτελείται από τα ακόλουθα μέρη:

• 4 μικροσωληνοειδή
• Ένας καθρέφτης 1/2 ιντσών
• Τέσσερις βίδες Μ3

Οι συγκεκριμένες ηλεκτρομαγνητικές βαλβίδες που χρησιμοποίησα αγοράστηκαν στο eBay για 1,45 $ η κάθε μία. Ο στρογγυλός καθρέφτης βρέθηκε στο διάδρομο χειροτεχνίας στο HobbyLobby - ένα πακέτο των 25 μου κόστισε λιγότερο από 3 δολάρια. Μπορείτε επίσης να βρείτε καθρέφτες στο eBay.

Θα χρειαστείτε επίσης έναν φθηνό δείκτη λέιζερ, πάλι, από το eBay. Ένα βιολετί λέιζερ μαζί με ένα λαμπερό φύλλο βινυλίου είναι ένας εξαιρετικός συνδυασμός για αυτό το έργο!

Ένα σύνολο βοηθητικών χεριών δεν είναι απαραίτητο, αλλά θα είναι πολύ χρήσιμο για τη συγκράτηση και τοποθέτηση του δείκτη λέιζερ. Ένα μεγάλο συνδετικό συνδετήρα μπορεί να χρησιμοποιηθεί για να κρατήσετε πατημένο το κουμπί λειτουργίας.

Θα χρειαστείτε ένα Arduino (χρησιμοποίησα ένα Arduino Nano) και έναν τρόπο οδήγησης των σωληνοειδών. Όπως δήλωσε ο VajkF στα σχόλια, θα μπορούσατε να χρησιμοποιήσετε προκατασκευασμένη γέφυρα H, όπως αυτές που βασίζονται στο L298 ή στο L9110. Αυτά είναι άμεσα διαθέσιμα στο eBay για λίγα δολάρια και μπορούν επίσης να χρησιμοποιηθούν για οδήγηση κινητήρων και ρομποτικών έργων.

Δεδομένου ότι δεν είχα γέφυρα H, έφτιαξα τον δικό μου οδηγό από διακριτά εξαρτήματα:

• Τέσσερα διπολικά τρανζίστορ NPN (χρησιμοποίησα MPS3704)
• Τέσσερις αντιστάσεις (χρησιμοποίησα αντίσταση 1,2k ohm)
• Τέσσερις δίοδοι (χρησιμοποίησα 1N4004)
• Μπαταρία 9V και υποδοχή μπαταρίας

Τα ηλεκτρονικά εξαρτήματα ήταν από το εργαστήριό μου, οπότε δεν έχω ακριβές κόστος για αυτά, αλλά αν δεν έχετε ήδη τα εξαρτήματα ή δεν μπορείτε να τα καθαρίσετε, είναι πιθανότατα πιο αποδοτικό να χρησιμοποιήσετε μια προκατασκευασμένη γέφυρα Η. Παρ 'όλα αυτά, θα σας δώσω τα σχήματα για τη δημιουργία του δικού σας.

Βήμα 2: Τρισδιάστατη εκτύπωση της μονάδας διεύθυνσης καθρέφτη

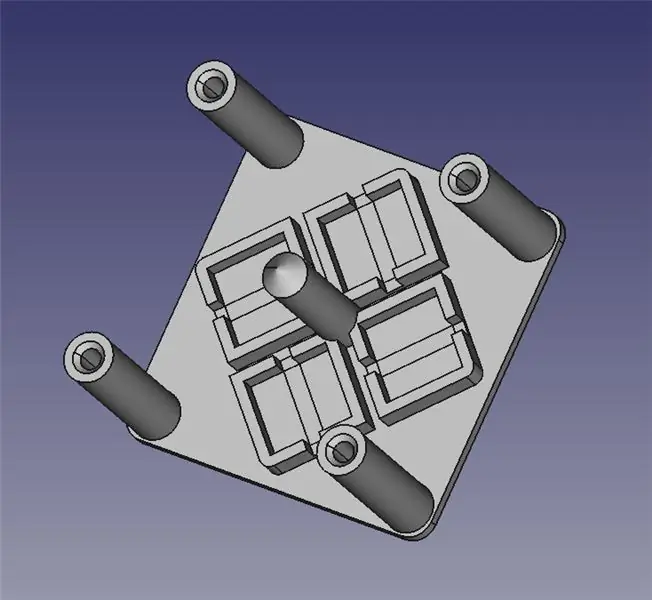
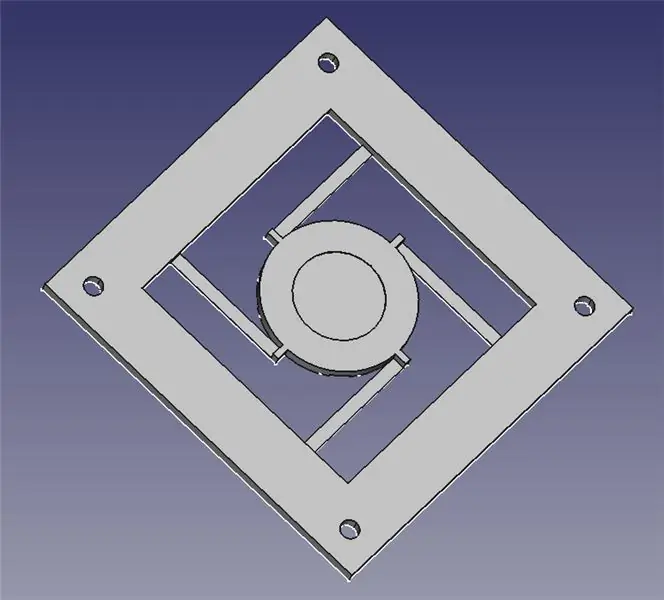
Η μονάδα διεύθυνσης λέιζερ αποτελείται από δύο τρισδιάστατα εκτυπωμένα μέρη: μια βάση για την τοποθέτηση τεσσάρων σωληνοειδών και μια αρθρωτή πλατφόρμα για τον καθρέφτη.

Σας έχω επισυνάψει τα δύο αρχεία STL σε τρισδιάστατη εκτύπωση, καθώς και αρχεία FreeCAD σε περίπτωση που χρειαστεί να τροποποιήσετε το σχέδιο. Όλο το περιεχόμενο βρίσκεται κάτω από το GPLv3, οπότε είστε ελεύθεροι να κάνετε και να μοιραστείτε τις βελτιώσεις σας!

Βήμα 3: Συναρμολογήστε τη μονάδα λέιζερ

• Χρησιμοποιήστε θερμή κόλλα για να τοποθετήσετε τις τέσσερις σωληνοειδείς στο κάτω κομμάτι.
• Χρησιμοποιήστε ζεστή κόλλα για να κολλήσετε τον καθρέφτη στο κέντρο του άνω κομματιού.
• Τοποθετήστε τα μεταλλικά έμβολα στις ηλεκτρομαγνητικές βαλβίδες και στη συνέχεια τοποθετήστε το επάνω κομμάτι στους στύλους (αλλά μην το βιδώσετε). Περιστρέψτε ελαφρά το επάνω κομμάτι και χρησιμοποιώντας ένα μικρό κατσαβίδι, σηκώστε κάθε έμβολο στη θέση του. Το χείλος του δίσκου πρέπει να γλιστρήσει μέσα στην αυλάκωση του εμβόλου. Προσοχή, καθώς οι μεντεσέδες με 3D εκτύπωση είναι πολύ εύθραυστοι. Με υπομονή και πιθανώς μερικές αποτυχημένες προσπάθειες, θα πρέπει να μπορείτε να τοποθετήσετε και τα τέσσερα έμβολα χωρίς να στρίψετε ή να ασκήσετε πίεση στους μεντεσέδες.
• Μόλις τοποθετηθούν όλα τα έμβολα, τοποθετήστε εν μέρει τις βίδες Μ3, αλλά πριν τις σφίξετε, πιέστε ελαφρά προς τα κάτω κάθε έμβολο και βεβαιωθείτε ότι ο καθρέφτης γέρνει ελεύθερα. Εάν δεν κινείται ελεύθερα ή πιάνει, μπορεί να χρειαστεί να αφαιρέσετε την επάνω πλάκα, να αφαιρέσετε μία ή περισσότερες σωληνοειδείς σωλήνες και να την επανασυνδέσετε σε μικρή εξωτερική γωνία (η τοποθέτηση αποστάσεων μεταξύ αυτής και της κεντρικής στύλας μπορεί να βοηθήσει σε αυτό) Το

Βήμα 4: Εκτυπώστε το κολάρο δείκτη λέιζερ

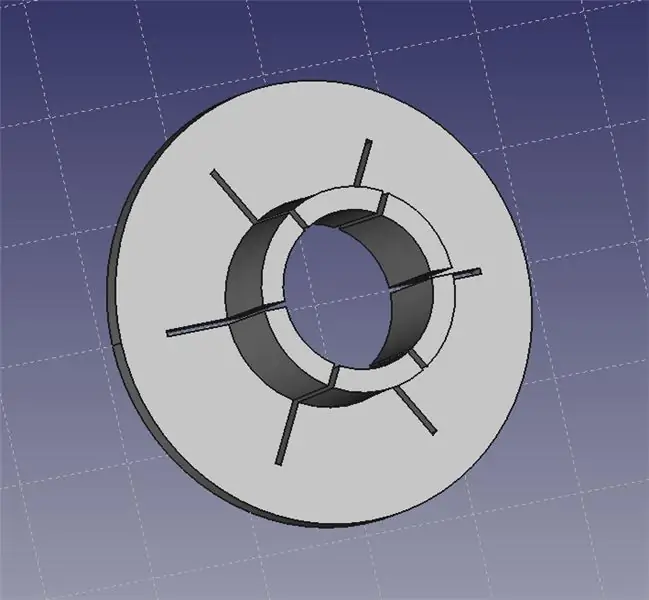
Το κολάρο του δείκτη λέιζερ ταιριάζει στην κεφαλή του δείκτη λέιζερ. Στη συνέχεια, μπορείτε να χρησιμοποιήσετε ένα σύνολο βοηθητικών χεριών για να πιάσετε το γιακά και να σας επιτρέψει να τοποθετήσετε το λέιζερ ακριβώς στον πάγκο σας.

Βήμα 5: Συναρμολογήστε το κύκλωμα οδήγησης

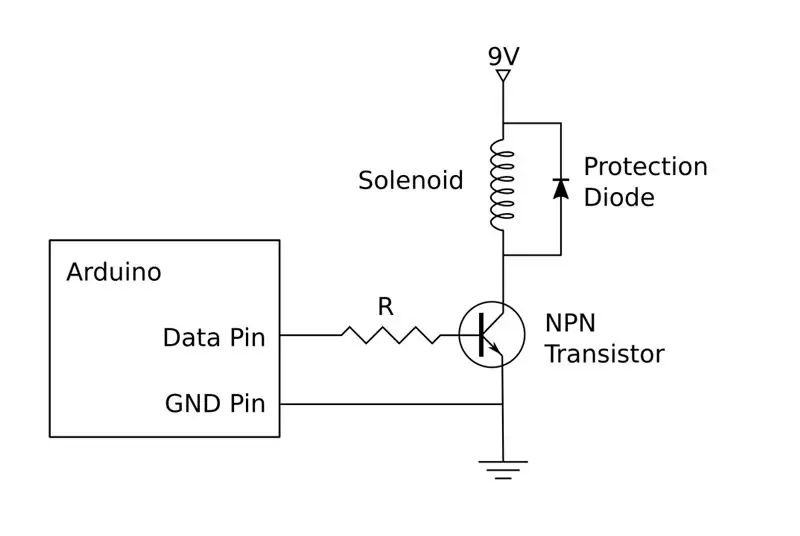
Το κύκλωμα κίνησης εμφανίζεται στο σχηματικό σχήμα. Όπως αναφέρθηκε προηγουμένως, η έκδοση μου είναι κατασκευασμένη από διακριτά στοιχεία, αλλά θα μπορούσατε επίσης να χρησιμοποιήσετε μια άμεσα διαθέσιμη γέφυρα H. Εάν επιλέξετε να δημιουργήσετε το δικό σας, θα χρειαστεί να δημιουργήσετε τέσσερα αντίγραφα αυτού του κυκλώματος, ένα για καθένα από τα τέσσερα σωληνοειδή.

Κάθε κύκλωμα θα συνδέεται με έναν πείρο Arduino, δύο για τον έλεγχο της αριστερής και της δεξιάς ηλεκτρομαγνητικής βαλβίδας και δύο για τις σωληνοειδείς πάνω και κάτω. Αυτά θα πρέπει να συνδεθούν με ακίδες με δυνατότητα PWM, όπως παρακάτω:

• Pin 9: Up Solenoid
• Pin 3: Down Solenoid
• Καρφίτσα 11: Αριστερή ηλεκτρομαγνητική βαλβίδα
• Καρφίτσα 10: Δεξιά σωληνοειδής

Μία μπαταρία 9V μπορεί να χρησιμοποιηθεί για την οδήγηση και των τεσσάρων κυκλωμάτων ηλεκτρομαγνητικών σωληνοειδών ή μπορείτε να χρησιμοποιήσετε τροφοδοτικό πάγκου. Το Arduino θα τελειώσει με την τροφοδοσία USB και δεν θα πρέπει να είναι συνδεδεμένο με τη θετική πλευρά της μπαταρίας των 9V. Ωστόσο, η αρνητική πλευρά της μπαταρίας χρησιμοποιείται ως σημείο αναφοράς γείωσης και πρέπει να συνδεθεί με τον πείρο GND στο Arduino καθώς και με τις ακίδες εκπομπής στα τρανζίστορ.

Βήμα 6: Ανεβάστε το δείγμα κώδικα

Το δείγμα κώδικα έχει ενημερωθεί με τις ακόλουθες δυνατότητες:

• Ρυθμίζει τη συχνότητα PWM έτσι ώστε ο μηχανισμός να είναι σχεδόν αθόρυβος σε χαμηλές ταχύτητες. Το βουητό στο Motion Test 1 έχει φύγει τελείως!
• Προσθέτει ως εξισώσεις τάσης με βάση το έγγραφο του Schimpf προκειμένου να "γραμμικοποιηθεί" η μη γραμμική απόκριση των ηλεκτρομαγνητικών σωληνοειδών.

Έχω συμπεριλάβει επίσης μια υλοποίηση ενός Lorenz Attractor με βάση τον κώδικα από αυτό το ιστολόγιο.

Η πιστότητα των αποτελεσμάτων αφήνει αρκετά επιθυμητά, αλλά το δουλεύω ακόμα!:)

Τα επόμενα βήματα απεικονίζουν μερικές από τις τεχνικές που χρησιμοποιούνται στον κώδικα.

Βήμα 7: Μείωση της έντασης

Στο Motion Test 1, μπορείτε να ακούσετε ένα δυνατό βουητό, ιδιαίτερα κατά τη διάρκεια της κίνησης πάνω και κάτω. Αποδεικνύεται ότι αυτό προκλήθηκε από την προεπιλεγμένη συχνότητα κοπής PWM του Arduino που ήταν εντός του ακουστικού εύρους. Η ταχεία ενεργοποίηση και απενεργοποίηση της τάσης του πηνίου θα τους προκαλούσε δόνηση σε αυτή τη συχνότητα, κάνοντάς τα μικρά μικρά μεγάφωνα.

Για να λύσω αυτό το πρόβλημα, αύξησα τη συχνότητα PWM στον κώδικα:

#define PWM_FREQ_31372Hz 0x01 // Ρυθμίζει τη συχνότητα PWM στα 31372.55 Hz #ορίζει PWM_FREQ_3921Hz 0x02 // Ρυθμίζει τη συχνότητα PWM σε 3921.16 Hz #define PWM_FREQ_980Hz 0x03 // Ρυθμίσεις PWMTM & 0b11111000) | συχνότητα; // Ρύθμιση χρονοδιακόπτη1 (ακίδες 9 & 10) συχνότητας TCCR2B = (TCCR2B & 0b11111000) | συχνότητα; // Ρύθμιση συχνότητας χρονοδιακόπτη2 (ακίδες 3 & 11)}

Η ρύθμιση της συχνότητας Arduino PWM είναι ένα χρήσιμο τέχνασμα για να απενεργοποιήσετε τις ηλεκτρομαγνητικές βαλβίδες ή τους κινητήρες. Πειραματιστείτε με τις διαφορετικές επιλογές συχνοτήτων για να δείτε ποια σας δίνει τα καλύτερα αποτελέσματα. Αν και περιλαμβάνει κάποιον πιο προηγμένο προγραμματισμό, ένας καλός πόρος για το πώς λειτουργούν τα χρονόμετρα είναι εδώ.

Βήμα 8: Ρύθμιση των τάσεων για μείωση της παραμόρφωσης

Οι αρχικές μου δοκιμές κίνησης έδειξαν ότι ήταν σημαντική παραμόρφωση στην απόκριση των σωληνοειδών. Στο Motion Test 3 (αριστερή εικόνα), αυτό που υποτίθεται ότι ήταν μια κυκλική σπείρα έγινε αντίθετα ένας ορθογώνιος ιστός με οδοντωτές άκρες.

Η επίλυση αυτού του προβλήματος απαιτούσε λίγα μαθηματικά, αλλά μπόρεσα να εντοπίσω ένα καταπληκτικό χαρτί στον ιστό που με βοήθησε να καταλάβω το πρόβλημα αρκετά καλά για να το λύσω στο λογισμικό.

Αυτό που ακολουθεί σας καθοδηγεί στη διαδικασία που πέρασα για να συντονίσω το σύστημα και να βελτιώσω την εμφάνιση των ιχνών που προκύπτουν!

Βήμα 9: Τελειοποίηση του Λογισμικού, Με Μαθηματικά

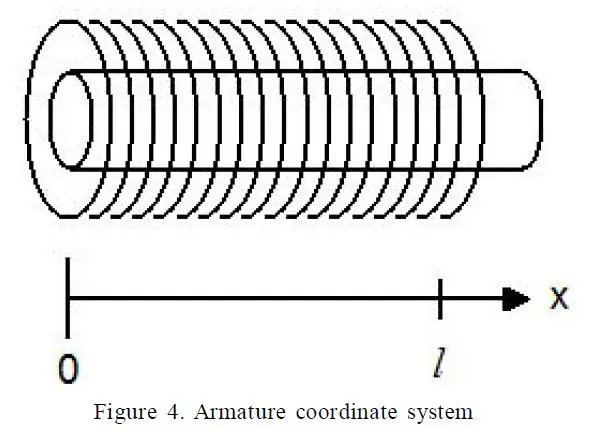
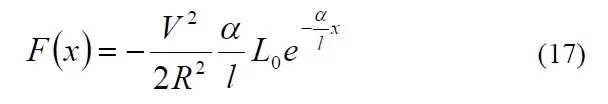
Το μυστικό για τη ρύθμιση του συστήματος αποδείχθηκε ότι ήταν ένα εξαιρετικό έγγραφο που ονομάζεται "A Detailed Explanation of Solenoid Force" από τον Paul H. Schimpf του Πανεπιστημίου Eastern Washington (σύνδεσμος). Συγκεκριμένα, η εξίσωση 17 μου έδωσε την ηλεκτρομαγνητική δύναμη από την άποψη διαφόρων όρων.

Οι παρακάτω όροι ήταν εύκολο να μετρηθούν:

• R - Η αντίσταση του σωληνοειδούς μου
• l - Το μήκος της ηλεκτρομαγνητικής βαλβίδας
• x - Η μετατόπιση του εμβόλου στην ηλεκτρομαγνητική βαλβίδα
• V - Η τάση στην ηλεκτρομαγνητική βαλβίδα

Knewξερα επίσης ότι η δύναμη που ασκεί η ηλεκτρομαγνητική βαλβίδα έπρεπε να εξισορροπήσει τη δύναμη από τα ελαστικά με 3D εκτύπωση στον καθρέφτη διπλού άξονα. Η δύναμη ενός ελατηρίου διέπεται από τον νόμο του Χουκ, ο οποίος αναφέρεται ως εξής:

F = -kx

Αν και δεν ήξερα την τιμή του k, τουλάχιστον ήξερα ότι η δύναμη που πήρα από την εξίσωση 17 από το χαρτί του Schimpf έπρεπε να ισούται με τη δύναμη του νόμου του Χουκ.

Η τιμή του άλφα (α) ήταν δύσκολη. Παρόλο που οι εξισώσεις 13 και 14 έδειξαν πώς να υπολογίσετε αυτές τις τιμές από την περιοχή της ηλεκτρομαγνητικής βαλβίδας (Α), τον αριθμό των στροφών (Ν) και τις τιμές μαγνητικής διαπερατότητας (μ), δεν ήθελα να χρειαστεί να σπάσω μια ηλεκτρομαγνητική βαλβίδα για να μετρήσω αριθμό στροφών, ούτε ήξερα το υλικό από το οποίο κατασκευάστηκε ο πυρήνας του ηλεκτρομαγνητικού μου.

Βήμα 10: Ένας φθηνός δοκιμαστής εξαρτημάτων σώζει την ημέρα

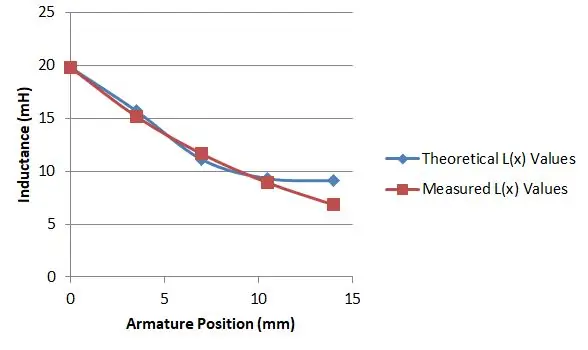
Αποδείχθηκε ωστόσο ότι η εξίσωση 15 και 16 μου έδωσε αυτό που χρειαζόμουν. Είχα έναν φθηνό ελεγκτή εξαρτημάτων M328 που είχα αγοράσει από το eBay για 10 $. Wasταν σε θέση να το χρησιμοποιήσει για να μετρήσει την επαγωγή του σωληνοειδούς μου και διαπίστωσα ότι σπρώχνοντας τον οπλισμό σε διαφορετικά βάθη μου έδωσε διαφορετικές τιμές επαγωγής.

Η μέτρηση του με τον οπλισμό πλήρως τοποθετημένο μου έδωσε την τιμή του L (0).

Το μήκος του σωληνοειδούς μου ήταν 14mm, οπότε μέτρησα την επαγωγή με τον οπλισμό σε πέντε θέσεις και αυτό μου έδωσε διάφορες τιμές για το L (x):

• L (0,0) = 19,8 mH
• L (3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L (14) = 9,1 mH

Στη συνέχεια χρησιμοποίησα ένα υπολογιστικό φύλλο για να σχεδιάσω τις τιμές μου έναντι της τιμής της εξίσωσης 15 και 16, για μια συγκεκριμένη επιλογή μr και στη συνέχεια άλλαξα την επιλογή μου μέχρι να βρω μια καλή αντιστοιχία. Αυτό συνέβη όταν το μr ήταν 2,9, όπως φαίνεται στο γράφημα.

Βήμα 11: Βρείτε τη Σταθερή άνοιξη Κ, λύστε το πρόβλημα

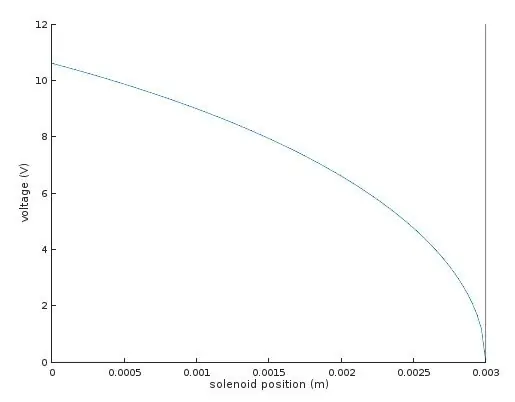
Το μόνο άγνωστο που απομένει ήταν το Κ, η σταθερά του ελατηρίου. Το μέτρησα εφαρμόζοντας 9V σε μία από τις ηλεκτρομαγνητικές βαλβίδες στη διάταξη διπλού άξονα και μετρώντας την απόσταση κατά την οποία ο καθρέφτης τραβήχτηκε προς τα κάτω. Με αυτές τις τιμές, μπόρεσα να λύσω τις εξισώσεις για το Κ, που διαπίστωσα ότι ήταν περίπου 10.41.

Είχα τώρα τις τιμές που χρειαζόμουν για να υπολογίσω το τράβηγμα της ηλεκτρομαγνητικής βαλβίδας σε διάφορες θέσεις κατά τη διάρκεια της διαδρομής. Ρυθμίζοντας το F (x) ίσο με τη δύναμη του ελατηρίου από το νόμο του Χουκ, μπορώ να λύσω για την απαιτούμενη τάση V.

Το γράφημα δείχνει την τάση που απαιτείται για τη μετακίνηση του σωληνοειδούς σε οποιαδήποτε επιθυμητή θέση x.

Στα δεξιά, όπου η τάση είναι μηδενική και η θέση είναι 3 mm, αυτό αντιστοιχεί στο ουδέτερο σημείο ανάπαυσης της ηλεκτρομαγνητικής βαλβίδας όταν οι μεντεσέδες που εκτυπώνονται 3D είναι πλήρως χαλαροί. Η κίνηση προς τα αριστερά στο γράφημα αντιστοιχεί στο τράβηγμα του οπλισμού στην ηλεκτρομαγνητική βαλβίδα ενάντια στο τράβηγμα των μεντεσέδων με τρισδιάστατη εκτύπωση-αυτό απαιτεί αρχικά περισσότερη τάση, αλλά καθώς ο οπλισμός μπαίνει βαθύτερα στο σωληνοειδές, η έλξη αυξάνεται και η απαιτούμενη τάση κίνησης μειώνεται.

Αυτή η σχέση είναι σίγουρα μη γραμμική, αλλά με τις εξισώσεις από το χαρτί του Schimpf, μπορώ να γράψω τον κωδικό Arduino μου για να βγάλει τις σωστές τάσεις, έτσι ώστε η εκτροπή της δέσμης να είναι γραμμική:

float positionToVoltage (float x) {

// Επαναφορά δύναμης που ασκείται από μεντεσέδες (Νόμος του Χουκ) στο επιθυμητό x. const float spring_F = -spring_K * (x - spring_X0); // Τάση τέτοια ώστε η δύναμη έλξης της ηλεκτρομαγνητικής βαλβίδας να αντιστοιχεί στην // δύναμη επαναφοράς των μεντεσέδων επιστρέφει sqrt (-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp (-a*x/solenoid_len))); }

Αυτό οδηγεί σε μια πολύ πιο κυκλική σπείρα από ό, τι στην αρχική δοκιμή κίνησης. Αποστολή εξετελέσθει!

Βήμα 12: Ερώτηση και απαντήσεις σχετικά με το κύκλωμα προγράμματος οδήγησης χρησιμοποιώντας διακριτά στοιχεία

Γιατί δεν μπορώ να συνδέσω την ηλεκτρομαγνητική βαλβίδα απευθείας στο Arduino;

Είναι θέμα του πόσο ρεύμα μπορεί να προσφέρει το Arduino χωρίς να υποστεί ζημιά. Αυτό είναι περίπου 40mA ανά καρφίτσα. Γνωρίζοντας ότι το Arduino λειτουργεί σε 5V, μπορούμε να χρησιμοποιήσουμε τον νόμο του Ohm για να υπολογίσουμε την απαιτούμενη ελάχιστη αντίσταση του φορτίου (στην περίπτωση αυτή, της ηλεκτρομαγνητικής βαλβίδας). Ο διαχωρισμός των 5 βολτ με 0,040 αμπέρ μας δίνει, 125 ωμ. Εάν το φορτίο έχει μεγαλύτερη αντίσταση, μπορούμε να το συνδέσουμε απευθείας με το Arduino, διαφορετικά δεν μπορούμε. Μια μικρή ηλεκτρομαγνητική βαλβίδα έχει συνήθως αντίσταση 50 ohm, οπότε δεν μπορούμε να την οδηγήσουμε απευθείας από το Arduino. Αν το κάναμε, θα τραβούσε 100mA, το οποίο είναι σαφώς υπερβολικό.

Γιατί χρησιμοποιείτε 9V για την ηλεκτρομαγνητική βαλβίδα, αλλά 5V για το Arduino;

Το Arduino λειτουργεί στα 5V, αλλά αυτό είναι λίγο πολύ για μια ηλεκτρομαγνητική βαλβίδα. Η χρήση ενός τρανζίστορ μας επιτρέπει να επιλέξουμε μια τάση για την ηλεκτρομαγνητική βαλβίδα που είναι ανεξάρτητη από τα 5V που χρησιμοποιούνται για το Arduino.

Πώς μπορώ να ξέρω εάν ένα τρανζίστορ είναι κατάλληλο για αυτό το έργο;

Ακριβώς όπως το Arduino, η κύρια απαίτηση είναι το ρεύμα που ρέει μέσω της ηλεκτρομαγνητικής βαλβίδας να μην υπερβαίνει τις μέγιστες ονομαστικές τιμές για το τρανζίστορ (συγκεκριμένα, το ρεύμα του συλλέκτη). Μπορούμε εύκολα να υπολογίσουμε το χειρότερο σενάριο μετρώντας την αντίσταση της ηλεκτρομαγνητικής βαλβίδας και στη συνέχεια διαιρώντας την τάση τροφοδοσίας με αυτήν. Στην περίπτωση ρεύματος τροφοδοσίας 9V για τις ηλεκτρομαγνητικές βαλβίδες και αντίστασης σωληνοειδών 50 ohms, το χειρότερο σενάριο μας βάζει στα 180mA. Το MPS3704, για παράδειγμα, έχει βαθμολογία για μέγιστο ρεύμα συλλέκτη 600 mA, το οποίο μας δίνει περιθώριο περίπου 3.

Πώς μπορώ να καθορίσω την ελάχιστη τιμή της αντίστασης που πρέπει να τεθεί μεταξύ της εξόδου του Arduino και της βάσης του τρανζίστορ;

Η έξοδος του Arduino θα συνδέσει το βασικό σκέλος των διπολικών τρανζίστορ μέσω μιας αντίστασης περιορισμού ρεύματος. Δεδομένου ότι το Arduino λειτουργεί σε 5V, μπορούμε πάλι να χρησιμοποιήσουμε το νόμο του Ohm για να υπολογίσουμε την απαιτούμενη αντίσταση για τον περιορισμό του ρεύματος κάτω από 40mA. Δηλαδή, διαιρέστε 5 βολτ με 0,04 αμπέρ για να λάβετε μια τιμή τουλάχιστον 125 ωμ. Υψηλότερες τιμές αντίστασης θα μειώσουν το ρεύμα, δίνοντάς μας έτσι ακόμη μεγαλύτερο περιθώριο ασφαλείας.

Υπάρχει μέγιστη τιμή για αυτήν την αντίσταση την οποία δεν πρέπει να υπερβώ;

Αποδεικνύεται, ναι. Ένα τρανζίστορ έχει αυτό που είναι γνωστό ως τρέχον κέρδος. Για παράδειγμα, εάν το κέρδος είναι 100, σημαίνει ότι αν βάλουμε 1mA στη βάση, τότε μέχρι 100mA θα ρέει μέσω του φορτίου που ελέγχει το τρανζίστορ. Εάν βάλουμε 1,8mA στη βάση, τότε μέχρι το 180mA θα ρέει μέσω του φορτίου. Δεδομένου ότι υπολογίσαμε νωρίτερα ότι στα 9V, 180mA ρέει μέσω της ηλεκτρομαγνητικής βαλβίδας, τότε ένα βασικό ρεύμα 1,8mA είναι το «γλυκό σημείο», και λιγότερο και το σωληνοειδές μας δεν θα ενεργοποιηθεί εντελώς.

Γνωρίζουμε ότι το Arduino βγάζει 5V και θέλουμε να ρεύσει 1,8mA, οπότε χρησιμοποιούμε τον νόμο του Ohm (R = V/I) για να υπολογίσουμε την αντίσταση (R = V/I). 5V διαιρούμενο με 1,8mA δίνει αντίσταση 2777 ohms. Επομένως, με βάση τις υποθέσεις που κάναμε, αναμένουμε ότι η αντίσταση πρέπει να κυμαίνεται μεταξύ 125 και 2777 - η επιλογή κάτι περίπου 1000 ωμ μας δίνει ένα αρκετά καλό περιθώριο ασφάλειας με κάθε τρόπο.

Βήμα 13: Ανάλυση τρέχοντων προβλημάτων και πιθανών λύσεων

Το τρέχον πρωτότυπο δείχνει δυνατότητες, αλλά παραμένουν αρκετά προβλήματα:

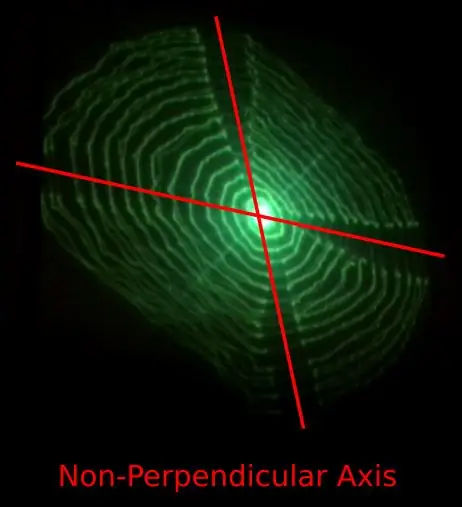
1. Η κίνηση κατά μήκος του άξονα Χ και Υ δεν φαίνεται να είναι κάθετη.
2. Υπάρχει άλμα όταν ο καθρέφτης αλλάζει κατεύθυνση.
3. Η ανάλυση είναι αρκετά χαμηλή και υπάρχουν ορατά μοτίβα σκαλοπατιών.
4. Σε υψηλότερες ταχύτητες κίνησης, η διαδρομή του λέιζερ παραμορφώνεται από κραδασμούς και κουδούνισμα.

Το ζήτημα 1) μπορεί να προκληθεί από το σχεδιασμό των τρισδιάστατων εκτυπωμένων εύκαμπτων μεντεσέδων που μεταδίδουν κίνηση κατά μήκος ενός άξονα στον κάθετο άξονα.

Το ζήτημα 2) οφείλεται στην χαλάρωση της σύζευξης μεταξύ των εμβόλων οδήγησης και της πλατφόρμας καθρέφτη, αυτό προκαλεί το σπασμωδικό καθρέφτη και παραλείπει στις μεταβάσεις μεταξύ του άξονα Χ και Υ. Αυτή η ξαφνική κίνηση οδηγεί σε ένα σκοτεινό κενό σε σχήμα Χ όπου η κουκκίδα λέιζερ κάνει μια ταχύτερη ανεξέλεγκτη κίνηση.

Τεύχος 3) συμβαίνει επειδή το προεπιλεγμένο Arduino PWM έχει μόνο 255 επίπεδα και αρκετά από αυτά χάνονται λόγω του σχήματος της καμπύλης τάσης. Αυτό θα μπορούσε να βελτιωθεί σημαντικά με τη χρήση του timer1, το οποίο είναι 16-bit και θα μπορούσε να έχει 65536 μοναδικές τιμές.

Τεύχος 4) συμβαίνει επειδή ο καθρέφτης και ο συρόμενος οπλισμός της ηλεκτρομαγνητικής βαλβίδας (έμβολα) αποτελούν σημαντική ποσότητα κινούμενης μάζας.

Καθώς τα ζητήματα 1) και 2) σχετίζονται με τον μηχανικό σχεδιασμό, μια πιθανότητα μπορεί να είναι η αφαίρεση των μεταλλικών εμβόλων και η αντικατάστασή τους με μικρούς μαγνήτες σπάνιας γης που είναι τοποθετημένοι απευθείας στην πλάκα κλίσης. Οι ηλεκτρομαγνητικές βαλβίδες θα ήταν ένα ανοιχτό πηνίο που θα προσελκύει ή θα απωθεί τους μαγνήτες χωρίς να κάνει φυσική επαφή. Αυτό θα οδηγούσε σε ομαλότερη κίνηση και θα εξαλείφει την πιθανότητα σπασμού, μειώνοντας παράλληλα τη συνολική μάζα.

Η μείωση της μάζας είναι η κύρια λύση για το ζήτημα 4), αλλά τυχόν εναπομείναντα προβλήματα θα μπορούσαν να στοχευθούν απευθείας στο λογισμικό εφαρμόζοντας ένα προφίλ ελέγχου κίνησης στο λογισμικό για επιτάχυνση και επιβράδυνση του καθρέφτη με ελεγχόμενο τρόπο. Αυτό έχει ήδη γίνει ευρέως στο υλικολογισμικό τρισδιάστατων εκτυπωτών και παρόμοιες μέθοδοι μπορεί να λειτουργήσουν και εδώ. Ακολουθούν ορισμένοι πόροι που σχετίζονται με τον έλεγχο κίνησης όπως ισχύει για τους 3D εκτυπωτές:

• "Μαθηματικά προφίλ ελέγχου κίνησης", Chuck Lewin (σύνδεσμος)
• "Jerk Controlled Motion Explained", (σύνδεσμος)

Υποψιάζομαι ότι η προσθήκη ενός τραπεζοειδούς προφίλ ελέγχου κίνησης θα επέτρεπε στον καθρέφτη να κινείται σε πολύ μεγαλύτερες ταχύτητες χωρίς τεχνουργήματα ήχων ή κραδασμών.

Βήμα 14: Μελλοντική εργασία και πιθανές εφαρμογές

Παρόλο που η ανάπτυξη λύσεων σε αυτά τα προβλήματα θα απαιτήσει αρκετή δουλειά, ελπίζω ότι αυτή η μονάδα διεύθυνσης δέσμης ανοιχτού κώδικα μπορεί να γίνει μια προσιτή εναλλακτική λύση για έργα που βασίζονται σε γαλβανόμετρα σε εφαρμογές όπως:

• Ένα φθηνό σόου με λέιζερ για DJ και VJ.
• Μια ηλεκτρομηχανική διανυσματική οθόνη για ένα vintage arcade παιχνίδι όπως το Vectrex.
• Ένας εκτυπωτής SLA 3D τύπου ρητίνης DIY που στο πνεύμα της κίνησης RepRap, μπορεί να εκτυπώσει τη δική του μονάδα διεύθυνσης λέιζερ.
• Digitalηφιακή μετατόπιση ή οπτική σταθεροποίηση εικόνας για κάμερες.

Δεύτερο Βραβείο στο Διαγωνισμό Arduino 2017