
Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:37.
- Τελευταία τροποποίηση 2025-01-23 14:39.



Σε αυτό το Instructable θα σας δείξω πώς να φτιάξετε ένα παιχνίδι Tic Tac Toe με AI χρησιμοποιώντας ένα Arduino. Μπορείτε είτε να παίξετε ενάντια στο Arduino είτε να παρακολουθήσετε το Arduino να παίζει εναντίον του.
Χρησιμοποιώ έναν αλγόριθμο που ονομάζεται "minimax algorithm", ο οποίος μπορεί να χρησιμοποιηθεί όχι μόνο για τη δημιουργία τεχνητής νοημοσύνης για το Tic Tac Toe, αλλά και για μια ποικιλία άλλων παιχνιδιών όπως το Four in a Row, τα πούλια ή ακόμα και το σκάκι. Παιχνίδια όπως το σκάκι είναι πολύ περίπλοκα και απαιτούν πολύ πιο εκλεπτυσμένες εκδόσεις του αλγορίθμου. Για το παιχνίδι Tic Tac Toe, μπορούμε να χρησιμοποιήσουμε την απλούστερη έκδοση του αλγορίθμου, η οποία ωστόσο είναι αρκετά εντυπωσιακή. Στην πραγματικότητα, το AI είναι τόσο καλό που είναι αδύνατο να νικήσεις το Arduino!
Το παιχνίδι είναι εύκολο να χτιστεί. Χρειάζεστε μόνο μερικά στοιχεία και το σκίτσο που έχω γράψει. Πρόσθεσα επίσης μια πιο λεπτομερή εξήγηση του αλγορίθμου, αν θέλετε να καταλάβετε πώς λειτουργεί.
Βήμα 1: Δημιουργήστε και παίξτε
Για να δημιουργήσετε το παιχνίδι Tic Tac Toe θα χρειαστείτε τα ακόλουθα στοιχεία:
- Ένα Arduino Uno
- 9 LED WS2812 RGB
- 9 κουμπιά
- μερικά καλώδια καλωδίων και βραχυκυκλωτήρων
Συνδέστε τα εξαρτήματα όπως φαίνεται στο σκίτσο Fritzing. Στη συνέχεια, ανεβάστε τον κωδικό στο Arduino σας.
Από προεπιλογή, το Arduino κάνει την πρώτη στροφή. Για να γίνουν τα πράγματα λίγο πιο ενδιαφέροντα, η πρώτη κίνηση επιλέγεται τυχαία. Μετά την πρώτη κίνηση, το Arduino χρησιμοποιεί τον αλγόριθμο minimax για να καθορίσει την καλύτερη δυνατή κίνηση. Ξεκινάτε ένα νέο παιχνίδι επαναφέροντας το Arduino.
Μπορείτε να παρακολουθήσετε το Arduino να «σκέφτεται» ανοίγοντας το Serial Monitor. Για κάθε πιθανή κίνηση, ο αλγόριθμος υπολογίζει μια βαθμολογία που υποδεικνύει εάν αυτή η κίνηση θα οδηγήσει σε νίκη (τιμή 10) ή απώλεια (τιμή -10) για το Arduino ή ισοπαλία (τιμή 0).
Μπορείτε επίσης να παρακολουθήσετε το Arduino να παίζει εναντίον του, σχολιάζοντας τη γραμμή "#define DEMO_MODE" στην αρχή του σκίτσου. Αν ανεβάσετε το τροποποιημένο σκίτσο, το Arduino κάνει την πρώτη κίνηση τυχαία και στη συνέχεια χρησιμοποιεί τον αλγόριθμο minimax για να καθορίσει την καλύτερη κίνηση για κάθε παίκτη σε κάθε στροφή.
Σημειώστε ότι δεν μπορείτε να κερδίσετε κόντρα στο Arduino. Κάθε παιχνίδι είτε θα τελειώσει ισόπαλο είτε θα χάσετε, αν κάνετε λάθος. Αυτό συμβαίνει επειδή ο αλγόριθμος επιλέγει πάντα την καλύτερη δυνατή κίνηση. Όπως ίσως γνωρίζετε, ένα παιχνίδι Tic Tac Toe θα καταλήγει πάντα ισόπαλο εάν και οι δύο παίκτες δεν κάνουν λάθος. Στη λειτουργία επίδειξης, κάθε παιχνίδι τελειώνει με ισοπαλία γιατί, όπως όλοι γνωρίζουμε, οι υπολογιστές δεν κάνουν ποτέ λάθη;-)
Βήμα 2: Ο αλγόριθμος Minimax

Ο αλγόριθμος αποτελείται από δύο στοιχεία: μια λειτουργία αξιολόγησης και μια στρατηγική αναζήτησης. Η συνάρτηση αξιολόγησης είναι μια συνάρτηση που αποδίδει μια αριθμητική τιμή στις θέσεις του πίνακα. Εάν η θέση είναι μια τελική θέση (δηλ. Μια θέση όπου ο μπλε παίκτης ή ο κόκκινος παίκτης έχει κερδίσει ή όπου κανένας παίκτης δεν έχει κερδίσει), η λειτουργία αξιολόγησης είναι πολύ απλή: Ας υποθέσουμε ότι το Arduino παίζει μπλε και ο άνθρωπος παίζει κόκκινο Το Εάν η θέση είναι μια νικήτρια θέση για το μπλε, η συνάρτηση εκχωρεί μια τιμή 10 σε αυτήν τη θέση. Εάν είναι μια νικήτρια θέση για το κόκκινο, η συνάρτηση εκχωρεί μια τιμή -10 στη θέση. και αν η θέση είναι ισοπαλία, η συνάρτηση εκχωρεί μια τιμή 0.
Όταν είναι η σειρά του Arduino, θέλει να επιλέξει μια κίνηση που μεγιστοποιεί την αξία της συνάρτησης αξιολόγησης, επειδή η μεγιστοποίηση της αξίας σημαίνει ότι θα προτιμήσει μια νίκη έναντι μιας ισοπαλίας (10 είναι μεγαλύτερη από 0) και θα προτιμήσει μια ισοπαλία από την ήττα (0 είναι μεγαλύτερη από -10). Με ανάλογο επιχείρημα, η αντίπαλος θέλει να παίξει με τέτοιο τρόπο ώστε να ελαχιστοποιεί την αξία της συνάρτησης αξιολόγησης.
Για μια μη τελική θέση, ο αλγόριθμος υπολογίζει την τιμή της συνάρτησης αξιολόγησης με μια αναδρομική στρατηγική αναζήτησης. Ξεκινώντας από την τρέχουσα θέση, προσομοιώνει εναλλάξ όλες τις κινήσεις που μπορεί να κάνει ο μπλε παίκτης και ο κόκκινος παίκτης. Αυτό μπορεί να απεικονιστεί ως δέντρο, όπως στο διάγραμμα. Όταν φτάσει σε μια τελική θέση, αρχίζει να κάνει πίσω, μεταφέροντας την αξία της συνάρτησης αξιολόγησης από το χαμηλότερο επίπεδο αναδρομής στο υψηλότερο επίπεδο αναδρομής. Εκχωρεί το μέγιστο (αν στο αντίστοιχο βήμα αναδρομής είναι η σειρά του μπλε παίκτη) ή το ελάχιστο (αν στο αντίστοιχο βήμα είναι η σειρά του κόκκινου παίκτη) των τιμών της συνάρτησης αξιολόγησης από το χαμηλότερο επίπεδο επανάληψης στη θέση υψηλότερο επίπεδο αναδρομής. Τέλος, όταν ο αλγόριθμος ολοκληρώσει το βήμα πίσω και φτάσει ξανά στην τρέχουσα θέση, χρειάζεται αυτή η κίνηση (ή μία από τις κινήσεις) που έχει τη μέγιστη τιμή της συνάρτησης αξιολόγησης.
Αυτό μπορεί να ακούγεται λίγο αφηρημένο, αλλά στην πραγματικότητα δεν είναι τόσο δύσκολο. Εξετάστε τη θέση που εμφανίζεται στην κορυφή του διαγράμματος. Στο πρώτο βήμα επαναφοράς, υπάρχουν τρεις διαφορετικές κινήσεις που μπορεί να κάνει το μπλε. Το μπλε προσπαθεί να μεγιστοποιήσει την τιμή της συνάρτησης αξιολόγησης. Για κάθε μία από τις κινήσεις που μπορεί να κάνει το μπλε, υπάρχουν δύο κινήσεις που μπορεί να κάνει το κόκκινο. Το κόκκινο προσπαθεί να ελαχιστοποιήσει την τιμή της συνάρτησης αξιολόγησης. Εξετάστε την κίνηση όπου παίζει το μπλε στην επάνω δεξιά γωνία. Εάν το κόκκινο παίζει στο κέντρο, το κόκκινο έχει κερδίσει (-10). Αν, από την άλλη πλευρά, το κόκκινο παίζει στο κεντρικό κάτω πλαίσιο, το μπλε θα κερδίσει στην επόμενη κίνηση (10). Έτσι, αν το μπλε παίζει στην επάνω δεξιά γωνία, το κόκκινο θα παίζει στο κεντρικό πλαίσιο, αφού αυτό ελαχιστοποιεί την τιμή της συνάρτησης αξιολόγησης. Αντίστοιχα, εάν το μπλε παίζει στο κεντρικό κάτω πλαίσιο, το κόκκινο θα παίξει ξανά στο κεντρικό πλαίσιο, επειδή αυτό ελαχιστοποιεί τη λειτουργία αξιολόγησης. Αν, από την άλλη πλευρά, το μπλε παίζει στο κέντρο, δεν έχει σημασία ποια κίνηση κάνει το κόκκινο, το μπλε θα κερδίζει πάντα (10). Δεδομένου ότι το μπλε θέλει να μεγιστοποιήσει τη συνάρτηση αξιολόγησης, θα παίξει στο κεντρικό πλαίσιο, καθώς αυτή η θέση έχει ως αποτέλεσμα μεγαλύτερη τιμή της συνάρτησης αξιολόγησης (10) από τις άλλες δύο κινήσεις (-10).
Βήμα 3: Αντιμετώπιση προβλημάτων και περαιτέρω βήματα
Εάν πιέσετε ένα κουμπί και ανάψει ένα διαφορετικό LED από αυτό που αντιστοιχεί στο κουμπί, πιθανότατα είτε μπλέξατε τα καλώδια στις ακίδες A0-A2 ή 4-6, είτε συνδέσατε τα LED με λάθος σειρά.
Σημειώστε επίσης ότι ο αλγόριθμος δεν επιλέγει πάντα μια κίνηση που θα αφήσει το Arduino να κερδίσει όσο το δυνατόν γρηγορότερα. Στην πραγματικότητα, πέρασα λίγο χρόνο για να διορθώσω τον αλγόριθμο επειδή το Arduino δεν επέλεξε μια κίνηση που θα ήταν μια νικηφόρα κίνηση. Μου πήρε λίγο χρόνο μέχρι να συνειδητοποιήσω ότι αντίθετα είχε επιλέξει μια κίνηση που εγγυάται ότι θα κερδίσει μία κίνηση αργότερα. Εάν θέλετε, μπορείτε να προσπαθήσετε να τροποποιήσετε τον αλγόριθμο έτσι ώστε να προτιμά πάντα μια νικηφόρα κίνηση από μια μεταγενέστερη νίκη.
Μια πιθανή επέκταση αυτού του έργου θα ήταν να χρησιμοποιήσετε τον αλγόριθμο για να δημιουργήσετε μια τεχνητή νοημοσύνη για 4x4 ή ακόμη και 5x5 Tic Tac Toe. Ωστόσο, σημειώστε ότι ο αριθμός των θέσεων που χρειάζεται να εξετάσει ο αλγόριθμος αυξάνεται πολύ γρήγορα. Θα χρειαστεί να βρείτε τρόπους για να κάνετε τη λειτουργία αξιολόγησης πιο έξυπνη, αντλώντας τιμές σε θέσεις που δεν είναι τελικές, με βάση την πιθανότητα η θέση να είναι καλή ή κακή για τον συγκεκριμένο παίκτη. Μπορεί επίσης να προσπαθήσετε να κάνετε την αναζήτηση πιο έξυπνη σταματώντας την αναδρομή νωρίς εάν μια κίνηση αποδειχθεί λιγότερο άξια περαιτέρω εξερεύνησης από τις εναλλακτικές κινήσεις.
Το Arduino πιθανότατα δεν είναι η καλύτερη πλατφόρμα για τέτοιες επεκτάσεις λόγω της περιορισμένης μνήμης του. Η αναδρομή αφήνει τη στοίβα να αναπτυχθεί κατά την εκτέλεση του προγράμματος και αν η στοίβα μεγαλώσει πολύ, μπορεί να καταστρέψει τη μνήμη του προγράμματος, οδηγώντας σε σφάλματα ή ακανόνιστη συμπεριφορά. Επέλεξα το Arduino για αυτό το έργο κυρίως επειδή ήθελα να δω αν θα μπορούσε να γίνει και για εκπαιδευτικούς σκοπούς, όχι επειδή είναι η καλύτερη επιλογή για αυτού του είδους το πρόβλημα.
Συνιστάται:
Self Balancing Robot - Αλγόριθμος ελέγχου PID: 3 βήματα

Self Balancing Robot - Αλγόριθμος Ελέγχου PID: Αυτό το έργο σχεδιάστηκε επειδή με ενδιέφερε να μάθω περισσότερα για τους Αλγόριθμους Ελέγχου και πώς να εφαρμόσω αποτελεσματικά λειτουργικούς βρόχους PID. Το έργο βρίσκεται ακόμη σε φάση ανάπτυξης καθώς δεν έχει ακόμη προστεθεί μια μονάδα Bluetooth η οποία θα
Παιχνίδι Arduino Touch Tic Tac Toe: 6 βήματα (με εικόνες)

Παιχνίδι Arduino Touch Tic Tac Toe: Αγαπητοί φίλοι καλώς ήρθατε σε ένα άλλο σεμινάριο Arduino! Σε αυτό το λεπτομερές σεμινάριο θα δημιουργήσουμε ένα παιχνίδι Arduino Tic Tac Toe. Όπως μπορείτε να δείτε, χρησιμοποιούμε οθόνη αφής και παίζουμε ενάντια στον υπολογιστή. Ένα απλό παιχνίδι όπως το Tic Tac Toe είναι
Κορδικός αλγόριθμος χρησιμοποιώντας VHDL: 4 βήματα
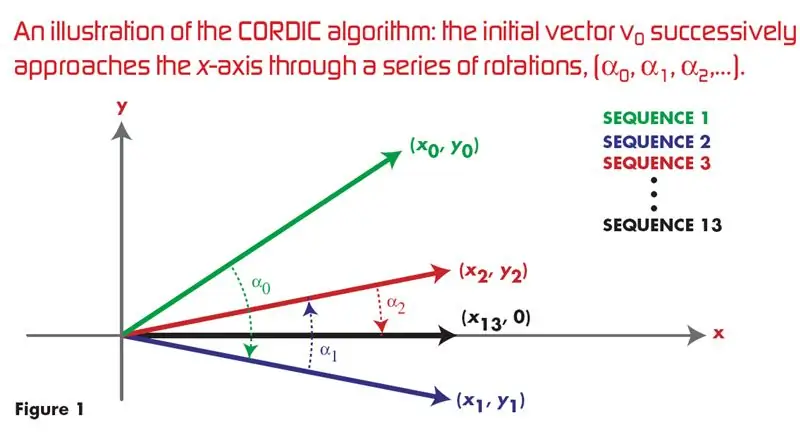
Cordic Algorithm Using VHDL: ## Αυτός είναι ο πιο δημοφιλής σύνδεσμος στο Google για εφαρμογή VHDL του CORDIC ALGORITHM για τη δημιουργία κυμάτων ημιτόνου και συνημίτονου ## Αυτή τη στιγμή υπάρχουν πολλοί αλγόριθμοι αποδοτικών υλικού, αλλά αυτοί δεν είναι πολύ γνωστοί κυριαρχία του μαλακού πολέμου
Επιτραπέζιο παιχνίδι Τεχνητή Νοημοσύνη: ο αλγόριθμος Minimax: 8 βήματα
Επιτραπέζιο παιχνίδι Τεχνητή Νοημοσύνη: ο αλγόριθμος Minimax: Αναρωτηθήκατε ποτέ πώς κατασκευάζονται οι υπολογιστές με τους οποίους παίζετε στο σκάκι ή στα πούλια; Λοιπόν, μην κοιτάξετε πέρα από αυτό το Instructable γιατί θα σας δείξει πώς να φτιάξετε μια απλή αλλά αποτελεσματική τεχνητή νοημοσύνη (AI) χρησιμοποιώντας τον αλγόριθμο Minimax! Χρησιμοποιώντας τη
Διαδραστικό παιχνίδι Tic-Tac Toe ελεγχόμενο με Arduino: 6 βήματα

Διαδραστικό παιχνίδι Tic-Tac Toe Controlled With Arduino: Ο στόχος του έργου Physical Tic-Tac-Toe είναι να μετακινήσει ένα γνωστό παιχνίδι στη φυσική σφαίρα. Αρχικά, το παιχνίδι παίζεται από δύο παίκτες σε ένα κομμάτι χαρτί - βάζοντας σύμβολα «Χ» και «Ο» σε στροφή. Η ιδέα μας ήταν να εξετάσουμε τη συμπεριφορά των παικτών
