Ρομπότ αυτοεξισορρόπησης χρησιμοποιώντας αλγόριθμο PID (STM MC): 9 βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:37

Πρόσφατα έχει γίνει πολλή δουλειά στην αυτοεξισορρόπηση αντικειμένων. Η έννοια της αυτοεξισορρόπησης ξεκίνησε με την εξισορρόπηση του ανεστραμμένου εκκρεμούς. Αυτή η ιδέα επεκτάθηκε και στον σχεδιασμό των αεροσκαφών. Σε αυτό το έργο, έχουμε σχεδιάσει ένα μικρό μοντέλο αυτόματου ρομπότ εξισορρόπησης χρησιμοποιώντας τον αλγόριθμο PID (αναλογικό, ολοκληρωμένο, παράγωγο). Από τότε, αυτή η μέθοδος είναι το νέο πρόσωπο των συστημάτων ελέγχου βιομηχανικής διαδικασίας. Αυτή η έκθεση εξετάζει τις μεθόδους που εμπλέκονται στην αυτοεξισορρόπηση αντικειμένων. Αυτό το έργο πραγματοποιήθηκε ως εξάμηνο για να κατανοήσει τη συσχέτιση του PID με την αποτελεσματικότητα των διαφόρων βιομηχανικών διαδικασιών. Εδώ εστιάζουμε μόνο στην παροχή μιας σύντομης ανασκόπησης για την αποτελεσματικότητα και την εφαρμογή του ελέγχου PID. Αυτή η εργασία αναπτύχθηκε παρέχοντας μια σύντομη εισαγωγή στα συστήματα ελέγχου και τις σχετικές ορολογίες, με προσθήκη στα κίνητρα για το έργο. Πραγματοποιήθηκαν πειραματισμοί και παρατηρήσεις, τα πλεονεκτήματα και τα μειονεκτήματα περιγράφονται με το τέλος των μελλοντικών βελτιώσεων. Ένα μοντέλο ρομπότ αυτο -εξισορρόπησης αναπτύχθηκε για να κατανοήσει την αποτελεσματικότητα του PID στον κόσμο του συστήματος ελέγχου. Περνώντας κάποιες αυστηρές δοκιμές και πειράματα, ανακαλύφθηκαν τα πλεονεκτήματα και τα μειονεκτήματα του συστήματος ελέγχου PID. Διαπιστώθηκε ότι παρά τα πολλά πλεονεκτήματα του ελέγχου PID έναντι παλαιότερων μεθόδων, αυτό το σύστημα εξακολουθεί να απαιτεί πολλές βελτιώσεις. Ελπίζουμε ότι ο αναγνώστης θα κατανοήσει καλά τη σημασία της αυτοεξισορρόπησης, την αποτελεσματικότητα και τις ανεπάρκειες του ελέγχου PID

Βήμα 1: Εισαγωγή

Με την έλευση των υπολογιστών και την εκβιομηχάνιση των διαδικασιών, σε όλη την ιστορία του ανθρώπου, υπήρχε πάντα έρευνα για την ανάπτυξη τρόπων για τον εντοπισμό διαδικασιών και το πιο σημαντικό, για τον αυτόματο έλεγχο αυτών. Ο σκοπός είναι να μειωθεί η εμπλοκή του ανθρώπου σε αυτές τις διαδικασίες, μειώνοντας έτσι το σφάλμα σε αυτές τις διαδικασίες. Ως εκ τούτου, αναπτύχθηκε το πεδίο "Μηχανική Συστήματος Ελέγχου". Η Μηχανική Συστήματος Ελέγχου μπορεί να οριστεί ως χρήση διαφόρων μεθόδων για τον έλεγχο της λειτουργίας μιας διαδικασίας ή συντήρησης ενός σταθερού και προτιμώμενου περιβάλλοντος, είτε χειροκίνητο είτε αυτόματο.

Ένα απλό παράδειγμα θα μπορούσε να είναι ο έλεγχος της θερμοκρασίας σε ένα δωμάτιο. Ο χειροκίνητος έλεγχος σημαίνει την παρουσία ενός ατόμου σε μια τοποθεσία που ελέγχει τις παρούσες συνθήκες (αισθητήρας), τη συγκρίνει με την επιθυμητή τιμή (επεξεργασία) και λαμβάνει τα κατάλληλα μέτρα για να αποκτήσει την επιθυμητή τιμή (ενεργοποιητής). Το πρόβλημα με αυτήν τη μέθοδο είναι ότι δεν είναι πολύ αξιόπιστο καθώς ένα άτομο είναι επιρρεπές σε λάθη ή αμέλεια στη δουλειά του. Επίσης, ένα άλλο πρόβλημα είναι ότι ο ρυθμός της διαδικασίας που ξεκινά από τον ενεργοποιητή δεν είναι πάντα ομοιόμορφος, που σημαίνει ότι μερικές φορές μπορεί να συμβεί γρηγορότερα από ό, τι απαιτείται ή μερικές φορές μπορεί να είναι αργός. Η λύση αυτού του προβλήματος ήταν η χρήση μικροελεγκτή για τον έλεγχο του συστήματος. Ο μικροελεγκτής είναι

προγραμματισμένο για τον έλεγχο της διαδικασίας, σύμφωνα με συγκεκριμένες προδιαγραφές, συνδεδεμένο σε ένα κύκλωμα (θα συζητηθεί αργότερα), τροφοδοτούσε την επιθυμητή τιμή ή συνθήκες και επομένως ελέγχει τη διαδικασία για να διατηρήσει την επιθυμητή τιμή. Το πλεονέκτημα αυτής της διαδικασίας είναι ότι δεν απαιτείται ανθρώπινη παρέμβαση σε αυτή τη διαδικασία. Επίσης, ο ρυθμός της διαδικασίας είναι ομοιόμορφος

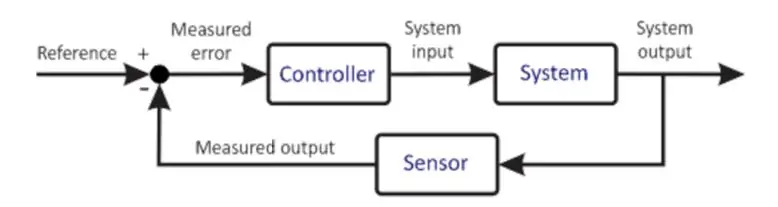
Βασικό Σύστημα Ελέγχου

Το προηγούμενο διάγραμμα δείχνει μια πολύ απλοποιημένη έκδοση ενός συστήματος ελέγχου. Ο μικροελεγκτής βρίσκεται στην καρδιά κάθε Συστήματος Ελέγχου. Είναι ένα πολύ σημαντικό συστατικό επομένως, η επιλογή της πρέπει να γίνει προσεκτικά με βάση τις απαιτήσεις του Συστήματος. Ο μικροελεγκτής λαμβάνει μια είσοδο από το χρήστη. Αυτή η είσοδος καθορίζει την επιθυμητή κατάσταση του συστήματος. Ο μικροελεγκτής λαμβάνει επίσης μια είσοδο ανάδρασης από τον αισθητήρα. Αυτός ο αισθητήρας είναι συνδεδεμένος στην έξοδο του συστήματος, οι πληροφορίες του οποίου επιστρέφονται στην είσοδο. Ο μικροεπεξεργαστής, με βάση τον προγραμματισμό του, εκτελεί διάφορους υπολογισμούς και δίνει έξοδο στον ενεργοποιητή. Ο ενεργοποιητής, με βάση την έξοδο, ελέγχει το εργοστάσιο για να προσπαθήσει να διατηρήσει αυτές τις συνθήκες. Ένα παράδειγμα θα μπορούσε να είναι ένας οδηγός κινητήρα που οδηγεί έναν κινητήρα όπου ο οδηγός κινητήρα είναι ο ενεργοποιητής και ο κινητήρας είναι η εγκατάσταση. Ο κινητήρας περιστρέφεται με συγκεκριμένη ταχύτητα. Ο συνδεδεμένος αισθητήρας διαβάζει την κατάσταση της εγκατάστασης αυτήν τη στιγμή και την τροφοδοτεί ξανά στον μικροελεγκτή. Ο μικροελεγκτής συγκρίνει ξανά, κάνει υπολογισμούς και έτσι, ο κύκλος επαναλαμβάνεται. Αυτή η διαδικασία είναι επαναλαμβανόμενη και ατελείωτη, όπου ο μικροελεγκτής διατηρεί τις επιθυμητές συνθήκες

Βήμα 2: Σύστημα ελέγχου βασισμένο σε PID

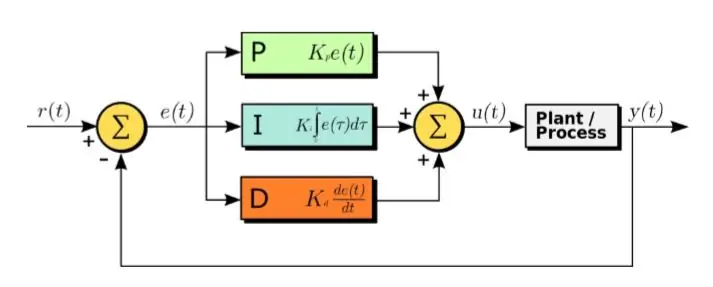
Ο αλγόριθμος PID είναι μια αποτελεσματική μέθοδος σχεδιασμού ενός συστήματος ελέγχου.

Ορισμός

Το PID σημαίνει Αναλογικό, Ολοκληρωτικό και Παράγωγο. Σε αυτόν τον αλγόριθμο, το σήμα σφάλματος που λαμβάνεται είναι η είσοδος. Και η ακόλουθη εξίσωση εφαρμόζεται στο σήμα σφάλματος

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ ολοκλήρωμα (e (t)) (1.1)

Σύντομη επεξήγηση

Όπως φαίνεται στην παραπάνω εξίσωση, το ολοκλήρωμα και το παράγωγο των σημάτων σφάλματος υπολογίζονται, πολλαπλασιάζονται με τις αντίστοιχες σταθερές τους και προστίθενται μαζί με τη σταθερά Kp πολλαπλασιασμένη με e (t). Η έξοδος τροφοδοτείται στη συνέχεια στον ενεργοποιητή που κάνει το σύστημα να λειτουργεί. Τώρα ας δούμε κάθε μέρος της συνάρτησης με τη σειρά. Αυτή η λειτουργία επηρεάζει άμεσα τον χρόνο ανόδου, τον χρόνο πτώσης, την κορυφή έναντι της βολής, τον χρόνο καθίζησης και το σφάλμα σταθερής κατάστασης.

• Αναλογικό μέρος: Το αναλογικό μέρος μειώνει το χρόνο ανόδου και μειώνει το σφάλμα σταθερής κατάστασης. Αυτό σημαίνει ότι το σύστημα θα πάρει λιγότερο χρόνο για να φτάσει στην κορυφαία τιμή του και όταν φτάσει στη σταθερή του κατάσταση, το σφάλμα σταθερής κατάστασης θα είναι χαμηλό. Ωστόσο, αυξάνει την υπέρβαση αιχμής.

• Παράγωγο μέρος: Το παράγωγο μέρος μειώνει την υπέρβαση και τον χρόνο καθίζησης. Αυτό σημαίνει ότι η παροδική κατάσταση του συστήματος θα είναι πιο αποσβεσμένη. Επίσης, το σύστημα θα φτάσει στη σταθερή του κατάσταση σε μικρότερο χρόνο. Ωστόσο, δεν έχει καμία επίδραση στον χρόνο ανόδου ή σφάλμα σταθερής κατάστασης.

• Αναπόσπαστο μέρος: Το αναπόσπαστο μέρος μειώνει τον χρόνο ανόδου και εξαλείφει εντελώς το σφάλμα σταθερής κατάστασης. Ωστόσο, αυξάνει την υπέρβαση αιχμής και τον χρόνο καθίζησης.

• Συντονισμός: Ένα καλό σύστημα ελέγχου θα έχει χαμηλό χρόνο ανόδου, χρόνο καθίζησης, μέγιστη υπέρβαση και σφάλμα σταθερής κατάστασης. Επομένως, τα Kp, Kd, Ki πρέπει να συντονιστούν για να προσαρμόσουν τη συμβολή των παραπάνω παραγόντων, προκειμένου να αποκτήσουν ένα καλό Σύστημα Ελέγχου.

Το σχήμα έχει επισυναφθεί που δείχνει την επίδραση της αλλαγής διαφόρων παραμέτρων στον αλγόριθμο PID.

Βήμα 3: Ρομπότ αυτοεξισορρόπησης

Ένα αυτορυθμιζόμενο ρομπότ είναι ένα πολυεπίπεδο ρομπότ με δύο τροχούς.

Το ρομπότ θα προσπαθήσει να ισορροπήσει με την εφαρμογή οποιασδήποτε άνισης δύναμης. Θα ισορροπήσει με την εφαρμογή δύναμης που αντιτίθεται στο αποτέλεσμα των δυνάμεων στο ρομπότ.

Μέθοδοι αυτοεξισορρόπησης

Υπάρχουν τέσσερις μέθοδοι αυτοεξισορρόπησης των ρομπότ. Αυτές είναι οι εξής:

Self Balancing χρησιμοποιώντας Two IR Tilt Sensor

Αυτός είναι ένας από τους πιο ωμούς τρόπους εξισορρόπησης του ρομπότ καθώς απαιτεί πολύ λιγότερο υλικό και σχετικά εύκολο αλγόριθμο. Σε αυτήν την προσέγγιση, χρησιμοποιούνται δύο κεκλιμένοι αισθητήρες IR για τη μέτρηση της απόστασης μεταξύ του εδάφους και του ρομπότ. Με βάση την απόσταση που υπολογίζεται, το PID μπορεί να χρησιμοποιηθεί για να οδηγήσει τους κινητήρες για να ισορροπήσει το ρομπότ ανάλογα. Ένα μειονέκτημα αυτής της μεθόδου είναι ότι ο αισθητήρας IR μπορεί να χάσει ορισμένες ενδείξεις. Ένα άλλο πρόβλημα είναι ότι απαιτείται διακοπή και βρόχοι για τον υπολογισμό της απόστασης που αυξάνει την πολυπλοκότητα του αλγορίθμου. Ως εκ τούτου, αυτή η μέθοδος εξισορρόπησης ρομπότ δεν είναι πολύ αποδοτική.

Self Balancing χρησιμοποιώντας επιταχυνσιόμετρο

Το επιταχυνσιόμετρο μας δίνει την επιτάχυνση του σώματος σε 3 άξονες. Η επιτάχυνση προσανατολισμένη στον άξονα y (προς τα πάνω) και στον άξονα x (προς τα εμπρός) μας δίνει το μέτρο για τον υπολογισμό της κατεύθυνσης της βαρύτητας και συνεπώς για τον υπολογισμό της γωνίας κλίσης. Η γωνία υπολογίζεται ως εξής:

θ = arctan (Ay/Ax) (1.2)

Το μειονέκτημα της χρήσης αυτής της μεθόδου είναι ότι κατά την κίνηση του ρομπότ, η οριζόντια επιτάχυνση θα προστεθεί επίσης στις ενδείξεις που είναι θόρυβος υψηλής συχνότητας. Ως εκ τούτου, η γωνία κλίσης θα είναι ανακριβής.

Self Balancing χρησιμοποιώντας γυροσκόπιο

Ένα γυροσκόπιο χρησιμοποιείται για τον υπολογισμό των ταχυτήτων γωνίας κατά μήκος των τριών αξόνων. Η γωνία κλίσης λαμβάνεται χρησιμοποιώντας την ακόλουθη εξίσωση.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

Ένα μεγάλο μειονέκτημα της χρήσης του γυροσκοπίου είναι ότι έχει μια μικρή DC Bias η οποία είναι θόρυβος χαμηλής συχνότητας και σε λίγη ώρα οι τιμές που επιστρέφονται είναι εντελώς λανθασμένες. Αυτό, μετά την ενσωμάτωση, θα προκαλέσει την απομάκρυνση του μηδενικού σημείου. Ως αποτέλεσμα, το ρομπότ θα παραμείνει στην κατακόρυφη θέση του για κάποιο χρονικό διάστημα και θα πέσει όταν έρθει η μετατόπιση.

Αυτοεξισορρόπηση χρησιμοποιώντας επιταχυνσιόμετρο και γυροσκόπιο

Όπως συζητήθηκε παραπάνω, η χρήση μόνο επιταχυνσιόμετρου ή γυροσκοπίου δεν θα μας δώσει τη σωστή γωνία κλίσης. Για να το εξηγήσουμε αυτό, χρησιμοποιούνται τόσο επιταχυνσιόμετρο όσο και γυροσκόπιο. Και τα δύο είναι ενσωματωμένα στο MPU6050. Σε αυτό λαμβάνουμε τα δεδομένα και από τους δύο και στη συνέχεια τα συγχωνεύουμε είτε χρησιμοποιώντας φίλτρο Kalman είτε συμπληρωματικό φίλτρο.

• Φίλτρο Kalman: Το φίλτρο Kalman υπολογίζει την καλύτερη εκτίμηση της κατάστασης ενός δυναμικού συστήματος από θορυβώδεις μετρήσεις, ελαχιστοποιώντας το μέσο τετραγωνικό σφάλμα της εκτίμησης. Λειτουργεί σε δύο στάδια, πρόβλεψη και διόρθωση, δεδομένων των διακριτών στοχαστικών εξισώσεων που περιγράφουν τη δυναμική του συστήματος. Ωστόσο, είναι ένας πολύ περίπλοκος αλγόριθμος που εφαρμόζεται ειδικά σε περιορισμένο υλικό μικροελεγκτή.

• Συμπληρωματικό φίλτρο: Αυτός ο αλγόριθμος χρησιμοποιεί κυρίως τα δεδομένα που λαμβάνονται από το γυροσκόπιο και τα ενσωματώνει με την πάροδο του χρόνου για να πάρει τη γωνία κλίσης. Χρησιμοποιεί επίσης ένα μικρό ποσοστό των μετρήσεων του επιταχυνσιόμετρου. Το συμπληρωματικό φίλτρο, στην πραγματικότητα, ελαχιστοποιεί τον θόρυβο υψηλής συχνότητας του επιταχυνσιόμετρου και τον θόρυβο χαμηλής συχνότητας του γυροσκοπίου και στη συνέχεια τα λιώνει για να δώσει την καλύτερη ακριβή γωνία κλίσης.

Βήμα 4: Σχεδιασμός ρομπότ

Έχουμε σχεδιάσει ένα ρομπότ αυτο -εξισορρόπησης χρησιμοποιώντας το Proportional Derivative controller που εφαρμόζεται από το Complementary Filter για MPU6050. Αυτό το μικρό μοντέλο του Self Balancing Robot θα μας δείξει τη χρησιμότητα των συστημάτων ελέγχου στο Self Balancing των ρομπότ.

Εφαρμογή συστήματος:

Το σύστημα είναι ένα ρομπότ αυτο -εξισορρόπησης. Εφαρμόζεται χρησιμοποιώντας τον ελεγκτή PID, ο οποίος είναι ένας αναλογικός ενσωματωμένος ελεγκτής παραγώγων. Ισορροπούμε το ρομπότ οδηγώντας τους τροχούς του προς την κατεύθυνση της πτώσης του. Με αυτόν τον τρόπο, προσπαθούμε να κρατήσουμε το κέντρο βάρους του ρομπότ πάνω από το σημείο περιστροφής. Για να οδηγήσουμε τους τροχούς προς την κατεύθυνση της πτώσης του, θα πρέπει να γνωρίζουμε πού πέφτει το ρομπότ και την ταχύτητα με την οποία πέφτει. Αυτά τα δεδομένα λαμβάνονται χρησιμοποιώντας MPU6050 που διαθέτει επιταχυνσιόμετρο και γυροσκόπιο. Το MPU6050 μετρά τη γωνία κλίσης και δίνει την έξοδο του στον μικροελεγκτή. Το MPU6050 διασυνδέεται με τον πίνακα STM μέσω I2C. Στο I2C, ένα καλώδιο είναι για το ρολόι που ονομάζεται SCL. Το άλλο είναι για τη μεταφορά δεδομένων που είναι SDA. Σε αυτό, χρησιμοποιείται επικοινωνία κύριου σκλάβου. Η διεύθυνση εκκίνησης και η τελική διεύθυνση είναι συγκεκριμένη για να γνωρίζουμε από πού ξεκινούν και πού τελειώνουν τα δεδομένα. Έχουμε εφαρμόσει το Συμπληρωματικό Φίλτρο εδώ για MPU6050 που είναι ένα μαθηματικό φίλτρο για τη συγχώνευση των εξόδων του επιταχυνσιόμετρου και του γυροσκοπίου. Μετά τη λήψη των δεδομένων από το MPU6050, ο μικροελεγκτής θα πραγματοποιήσει υπολογισμούς για να γνωρίζει πού πέφτει. Με βάση τους υπολογισμούς, ο μικροελεγκτής STM θα δώσει εντολές στον οδηγό του κινητήρα να οδηγήσει τα οχήματα προς την κατεύθυνση της πτώσης που θα ισορροπήσει το ρομπότ.

Βήμα 5: Στοιχεία έργου

Τα ακόλουθα στοιχεία χρησιμοποιήθηκαν στο έργο ρομπότ αυτο -εξισορρόπησης:

STM32F407

Ένας μικροελεγκτής σχεδιασμένος από την ST Microelectronics. Λειτουργεί στην αρχιτεκτονική ARM Cortex-M.

Πρόγραμμα οδήγησης κινητήρα L298N

Αυτό το IC χρησιμοποιείται για τη λειτουργία του κινητήρα. Παίρνει δύο εξωτερικές εισόδους. Ένας από τον μικροελεγκτή που του παρέχει σήμα PWM. Ρυθμίζοντας το πλάτος του παλμού, μπορείτε να ρυθμίσετε την ταχύτητα του κινητήρα. Η δεύτερη είσοδός του είναι η πηγή τάσης που απαιτείται για την οδήγηση του κινητήρα, η οποία είναι μια μπαταρία 12V στην περίπτωσή μας.

DC Motor

Ένα DC Motor λειτουργεί με τροφοδοσία DC. Σε αυτό το πείραμα, το DC Motor λειτουργεί με τη χρήση των οπτικών ζεύξεων που είναι συνδεδεμένα στο πρόγραμμα οδήγησης του κινητήρα. Για την οδήγηση του κινητήρα χρησιμοποιήσαμε το Motor Drive L298N.

MPU6050

Το MPU6050 χρησιμοποιείται για τη λήψη πληροφοριών σχετικά με το πού πέφτει το ρομπότ. Μετρά τη γωνία κλίσης ως προς το σημείο μηδενικής κλίσης που είναι η θέση του MPU6050 όταν το πρόγραμμα αρχίζει να τρέχει.

Το MPU6050 διαθέτει επιταχυνσιόμετρο 3 αξόνων και γυροσκόπιο 3 αξόνων. Το επιταχυνσιόμετρο μετρά την επιτάχυνση κατά μήκος των τριών αξόνων και το γυροσκόπιο μετρά τη γωνιακή ταχύτητα των τριών αξόνων. Για να συνδυάσουμε την έξοδο, πρέπει να φιλτράρουμε τους θορύβους και των δύο. Για να φιλτράρετε τους θορύβους, έχουμε το Kalman και το Συμπληρωματικό φίλτρο. Έχουμε εφαρμόσει συμπληρωματικό φίλτρο στο έργο μας.

Opto Couple 4N35

Το οπτικό ζεύγος είναι μια συσκευή που χρησιμοποιείται για την απομόνωση του τμήματος χαμηλής τάσης και του τμήματος υψηλής τάσης του κυκλώματος. Όπως υποδηλώνει το όνομα, λειτουργεί με βάση το φως. Όταν το τμήμα χαμηλής τάσης λαμβάνει σήμα, ρέει ρεύμα στο τμήμα υψηλής τάσης

Βήμα 6: Δομή του ρομπότ

Η δομή του ρομπότ εξηγείται ως εξής:

Φυσική δομή

Το αυτορυθμιζόμενο ρομπότ αποτελείται από δύο στρώματα που αποτελούνται από διαφανές πλαστικό γυαλί. Οι λεπτομέρειες δύο στρωμάτων δίνονται παρακάτω:

Πρώτο στρώμα

Στο κάτω μέρος του πρώτου στρώματος, έχουμε τοποθετήσει ένα κελί για την τροφοδοσία της πλακέτας STM. Επίσης δύο κινητήρες 4 βολτ έκαστος έχουν τοποθετηθεί σε κάθε πλευρά με ελαστικά συνδεδεμένα για να κινείται το ρομπότ. Στο επάνω μέρος του πρώτου στρώματος, έχουν τοποθετηθεί δύο μπαταρίες 4 βολτ έκαστη (συνολικά 8 βολτ) και οδηγός κινητήρα IC (L298N) για τη λειτουργία των κινητήρων.

Δεύτερο στρώμα

Στο επάνω στρώμα του ρομπότ, έχουμε τοποθετήσει τον πίνακα STM στο Perf Board. Ένας άλλος πίνακας τεσσάρων συζεύξεων opto τοποθετείται στο επάνω στρώμα. Το γυροσκόπιο τοποθετείται επίσης στο πάνω στρώμα του ρομπότ από την κάτω πλευρά. Και τα δύο εξαρτήματα τοποθετούνται στο μεσαίο τμήμα έτσι ώστε το κέντρο βάρους να διατηρείται όσο το δυνατόν χαμηλότερα.

Κέντρο βάρους του ρομπότ

Το κέντρο βάρους διατηρείται όσο το δυνατόν χαμηλότερα. Για το σκοπό αυτό, έχουμε τοποθετήσει βαριές μπαταρίες στο κάτω στρώμα και ελαφριά εξαρτήματα όπως η πλακέτα STM και τα οπτικά ζεύγη στο επάνω στρώμα.

Βήμα 7: Κωδικός

Ο κώδικας καταρτίστηκε στο Atollic TrueStudio. Το στούντιο STM χρησιμοποιήθηκε για σκοπούς εντοπισμού σφαλμάτων.

Βήμα 8: Συμπέρασμα

Μετά από πολλούς πειραματισμούς και παρατηρήσεις, φτάνουμε τελικά στο σημείο όπου συνοψίζουμε τα αποτελέσματά μας και συζητάμε πόσο μακριά καταφέραμε να εφαρμόσουμε και να επεξεργαστούμε την αποτελεσματικότητα του συστήματος.

Γενική ανασκόπηση

Κατά τη διάρκεια του πειραματισμού, η ταχύτητα του κινητήρα ελέγχθηκε επιτυχώς χρησιμοποιώντας τον αλγόριθμο PID. Η καμπύλη ωστόσο δεν είναι ακριβώς μια ομαλή ευθεία. Υπάρχουν πολλοί λόγοι για αυτό:

• Ο αισθητήρας, αν και συνδεδεμένος σε φίλτρο χαμηλής διέλευσης, εξακολουθεί να παρέχει ορισμένες ντεμπούτες. αυτά οφείλονται στις μη γραμμικές αντιστάσεις και σε ορισμένους αναπόφευκτους λόγους των αναλογικών ηλεκτρονικών.

• Ο κινητήρας δεν περιστρέφεται ομαλά υπό μικρή τάση ή PWM. Παρέχει τραντάγματα που ενδέχεται να προκαλέσουν λανθασμένες τιμές που τροφοδοτούνται στο σύστημα.

• Λόγω της ταλάντευσης, ο αισθητήρας μπορεί να χάσει ορισμένες σχισμές παρέχοντας υψηλότερες τιμές. • Ένας άλλος σημαντικός λόγος για σφάλματα μπορεί να είναι η συχνότητα του κεντρικού ρολογιού του μικροελεγκτή STM. Αυτό το μοντέλο μικροελεγκτή STM παρέχει ένα βασικό ρολόι 168MHz. Αν και αντιμετωπίστηκε αυτό το πρόβλημα σε αυτό το έργο, υπάρχει μια γενική αντίληψη για αυτό το μοντέλο ότι δεν παρέχει ακριβώς τόσο υψηλή συχνότητα.

Η ταχύτητα ανοιχτού βρόχου παρέχει μια πολύ ομαλή γραμμή με μερικές μόνο απροσδόκητες τιμές. Ο αλγόριθμος PID λειτουργεί επίσης, παρέχοντας πολύ χαμηλό χρόνο καθίζησης του κινητήρα. Ο αλγόριθμος PID του κινητήρα δοκιμάστηκε υπό διάφορες τάσεις διατηρώντας σταθερή την ταχύτητα αναφοράς. Η αλλαγή τάσης δεν αλλάζει την ταχύτητα του κινητήρα, δείχνοντας ότι ο αλγόριθμος PID λειτουργεί άψογα

Αποτελεσματικότητα

Εδώ συζητάμε για την αποτελεσματικότητα του ελεγκτή PID που παρατηρήσαμε κατά τη διάρκεια του πειραματισμού.

Απλή εφαρμογή

Έχουμε δει στην ενότητα πειραματισμών και παρατηρήσεων ότι ένας ελεγκτής PID είναι πολύ εύκολο να εφαρμοστεί. Απαιτεί μόνο τρεις παραμέτρους ή σταθερές που πρέπει να ρυθμιστούν για να υπάρχει σύστημα ελέγχου ταχύτητας

Ασύγκριτη αποδοτικότητα για γραμμικά συστήματα

Ο γραμμικός ελεγκτής PID είναι ο πιο αποτελεσματικός στην οικογένεια των ελεγκτών, επειδή η λογική είναι πολύ απλή και η εφαρμογή είναι ευρέως διαδεδομένη σε περίπτωση γραμμικών ή αρκετά γραμμικών εφαρμογών.

Περιορισμοί

Εξηγήσαμε αφηρημένα για τους Περιορισμούς αυτού του συστήματος. Εδώ συζητάμε μερικά από αυτά που παρατηρήσαμε.

Επιλογή σταθερών

Έχουμε δει ότι, αν και ένας ελεγκτής PID είναι εύκολο να εφαρμοστεί, εξακολουθεί να είναι ένα σημαντικό μειονέκτημα του συστήματος ότι το βήμα της επιλογής της τιμής των σταθερών είναι επίπονο. καθώς κάποιος πρέπει να κάνει δύσκολους υπολογισμούς. Ο άλλος τρόπος είναι η μέθοδος χτυπήματος και δοκιμής, αλλά επίσης δεν είναι αποτελεσματική.

Οι σταθερές δεν είναι πάντα σταθερές

Τα πειραματικά αποτελέσματα έδειξαν ότι για διαφορετικές τιμές της ταχύτητας αναφοράς για τον κινητήρα, ο ελεγκτής PID δυσλειτουργούσε για τις ίδιες τιμές των σταθερών PID. Για διαφορετικές ταχύτητες, οι σταθερές έπρεπε να επιλεγούν διαφορετικά και αυτό αυξάνει το υπολογιστικό κόστος εκθετικά.

Μη γραμμική

Ο ελεγκτής PID που χρησιμοποιείται στην περίπτωσή μας είναι γραμμικός, επομένως, μπορεί να εφαρμοστεί μόνο σε γραμμικά συστήματα. Για μη γραμμικά συστήματα, ο ελεγκτής πρέπει να εφαρμόζεται διαφορετικά. Παρόλο που διατίθενται διαφορετικές μη γραμμικές μέθοδοι PID, απαιτούν περισσότερες παραμέτρους για να επιλεγούν. Αυτό και πάλι καθιστά το σύστημα ανεπιθύμητο λόγω του υψηλού υπολογιστικού κόστους.

Απαιτείται αρχική ώθηση

Δείξαμε στην ενότητα πειραματισμού ότι για μια σχετικά μικρή ταχύτητα αναφοράς όπου το σφάλμα είναι αρκετά μικρό στην αρχή, το PWM που παρέχεται από το PID είναι τόσο μικρό που δεν δημιουργεί την απαιτούμενη ροπή εκκίνησης για τον κινητήρα. Έτσι, ο κινητήρας σε ορισμένες δοκιμές δεν λειτουργεί ή σε άλλες δοκιμές παρέχει μεγάλη υπέρβαση και μεγαλύτερο χρόνο καθίζησης.

Βήμα 9: Ιδιαίτερες ευχαριστίες

Ευχαριστώ ιδιαίτερα τα μέλη της ομάδας μου που με βοήθησαν σε αυτό το έργο.

Σύντομα θα ανεβάσω τον σύνδεσμο στο βίντεο.

Ελπίζω να βρείτε αυτό το διδακτικό ενδιαφέρον.

Αυτός είναι ο Tahir Ul Haq από την εγγραφή UET. Στην υγειά σας !!!