
Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:34.
- Τελευταία τροποποίηση 2025-01-23 14:39.

Η δημιουργία και των 7 βασικών λογικών πύλων στο Excel δεν είναι πολύ δύσκολη. Εάν κατανοείτε τις λειτουργίες στο Excel, τότε αυτό το έργο θα ήταν αρκετά απλό, αν δεν το κάνετε, μην ανησυχείτε δεν θα αργήσει να συνηθίσετε.
Το Excel έχει ήδη δημιουργήσει μερικές λογικές πύλες για εμάς, αλλά δεν περιλαμβάνει και τα 7 και έτσι κι αλλιώς θέλουμε να το φτιάξουμε μόνοι μας.
Το έργο δεν διαρκεί πολύ και μόλις ολοκληρωθεί, μπορείτε να δημιουργήσετε πολλά κυκλώματα ψηφιακά στο Excel.
Βήμα 1: Αυτό που χρειάζεστε
Δεν χρειάζεστε πολλά για αυτό το έργο.
- Υπολογιστή
- Excel (προτείνω το Excel αλλά παρόμοια θα πρέπει επίσης να είναι καλά)
- Βασικές γνώσεις για το πώς λειτουργούν οι λογικές πύλες
Βήμα 2: Ρύθμιση του Excel και της μορφοποίησης

Πρώτα ξεκινήστε το Excel (Η έκδοση δεν πρέπει να έχει μεγάλη σημασία, αλλά χρησιμοποίησα το Excel 2016) και, στη συνέχεια, ανοίξτε ένα νέο "Κενό βιβλίο εργασίας".
Στη συνέχεια, κάντε τη μορφή που βλέπετε στην παραπάνω εικόνα (Λόγω του σχήματος της εικόνας, θα πρέπει να κάνετε κλικ σε αυτήν για να την δείτε σωστά, αυτό ισχύει για τις παρακάτω εικόνες). Εάν δεν μπορείτε να αντιγράψετε τη μορφή, διαβάστε τα παρακάτω:
Κάντε τη στήλη B & C πλάτος ενός ψηφίου, συγχωνεύστε τη σειρά 1 A, B & C.
Στη συνέχεια, πληκτρολογήστε το κείμενο.
Βήμα 3: ΚΑΙ Πύλη
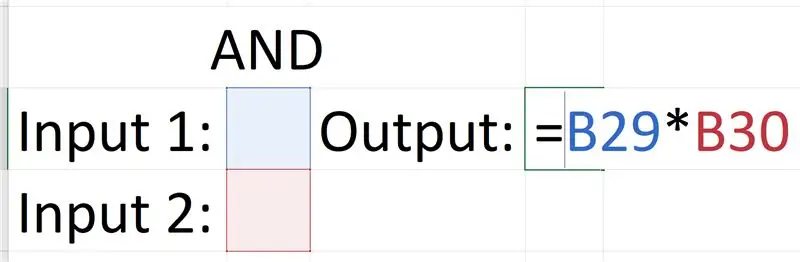
Η πύλη AND είναι η πιο απλή, αυτό συμβαίνει επειδή μπορείτε να πάρετε την έξοδο πολλαπλασιάζοντας τις εισόδους.
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1
Αυτό το προϊόν της εξίσωσης είναι το ίδιο με τις εξόδους της πύλης.
Αντιγράψτε τον τύπο και δοκιμάστε τον δίνοντάς του τις εισόδους (μόνο σε δυαδική μορφή).
Θυμηθείτε κάθε φορά που δημιουργείτε μια νέα πύλη, αντιγράψτε τη διάταξη ώστε να μην επικαλύπτεται τίποτα.
Βήμα 4: OR Πύλη
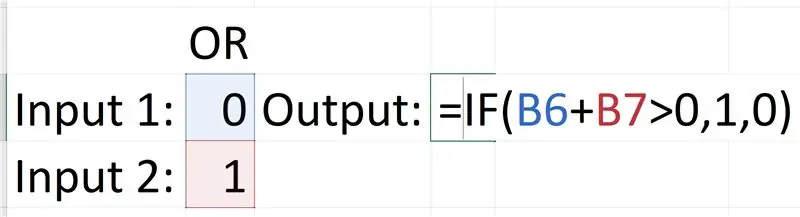
Η πύλη OR είναι πιο περίπλοκη, απαιτεί μια δήλωση "Εάν". Η δήλωση "Εάν" λειτουργεί ως εξής: = Εάν (λογική_ελέγχη, [τιμή εάν είναι αληθής], [τιμή εάν είναι ψευδής]). Το λογικό τεστ που χρησιμοποιούμε είναι: Είσοδος1 + Είσοδος2> 0, η πραγματική τιμή είναι 1, αλλιώς η τιμή είναι 0. Αυτό συμβαίνει γιατί μόνο εάν και οι δύο είσοδοι είναι ψευδείς, η έξοδος θα γίνει ψευδής και από 0 + 0 = 0, οτιδήποτε το σύνολο εισροών συμπεριλαμβανομένου του 1 θα είναι μεγαλύτερο σε αξία (άθροισμα αξία). Έτσι, εάν το άθροισμα και των δύο εισόδων είναι μεγαλύτερο από 0, τότε το out out του είναι True ή 1.
Βήμα 5: Πύλη NAND

Η πύλη NAND είναι ακριβώς όπως η πύλη OR, απαιτεί μια δήλωση "Εάν" και η λογική πίσω από αυτήν είναι παρόμοια. Η πύλη θα δώσει μια έξοδο False μόνο εάν και οι δύο είσοδοι είναι True. Έτσι, εάν πολλαπλασιάσουμε και τις δύο εισόδους, κάθε άθροισμα μικρότερο από 1 θα είναι αληθές, επειδή η δήλωση "Αν" είναι: input1 x input2 <1, 1, 0. Εάν αυτό ήταν μπερδεμένο, τότε αυτό το γράφημα μπορεί να βοηθήσει:
0 x 0 = 0, 0 <1 τόσο αληθινό = 1
0 x 1 = 0, 0 <1 τόσο αληθινό = 1
1 x 0 = 0, 0 <1 τόσο αληθινό = 1
1 x 1 = 1, 1 = 1 τόσο Λάθος = 0
Βήμα 6: NOR Gate

Η πύλη NOR χρησιμοποιεί επίσης μια δήλωση "Αν", η δήλωση για αυτήν την πύλη είναι: Εισαγωγή1 + Είσοδος2 <1, 1, 0. Αυτό συμβαίνει επειδή η πύλη δίνει μόνο μια True έξοδο και των δύο εισόδων είναι ψευδείς. Δεδομένου ότι προσθέτουμε και τις δύο εισόδους μαζί, κάθε σύνολο εισόδων συμπεριλαμβανομένου του 1 θα είναι μεγαλύτερο από δύο 0. Στη συνέχεια, η δήλωση Σωστό και Λάθος δείχνει ότι εάν οποιοδήποτε άθροισμα μικρότερο από 1, δείξτε 1 αλλιώς 0.
0 + 0 = 0, 0 <1 τόσο αληθινό = 1
0 + 1 = 1, 1 = 1 τόσο Λάθος = 0
1 + 0 = 1, 1 = 1 τόσο Λάθος = 0
1 + 1 = 2, 2> 1 τόσο Λάθος = 0
Βήμα 7: Πύλη XOR

Αυτό είναι αρκετά παρόμοιο με την πύλη NOR, αλλά αντί να χρησιμοποιήσουμε ένα μεγαλύτερο ή μικρότερο από το σύμβολο, χρησιμοποιούμε ένα σύμβολο ίσον επειδή η πύλη θα δώσει μόνο μια True έξοδο από αυτήν έχει μικτές εισόδους, οπότε αν προσθέσουμε και τις δύο εισόδους μαζί, μικτές εισόδους θα δίνει πάντα ένα 1 οπότε χρησιμοποιούμε τη δήλωση: Εισαγωγή1 + Είσοδος2 = 1, 1, 0.
0 + 0 = 0, 0 ≠ 1 τόσο Λάθος = 0
0 + 1 = 1, 1 = 1 τόσο αληθές = 1
1 + 0 = 1, 1 = 1 τόσο αληθές = 1
1 + 1 = 2, 2 ≠ 1 τόσο Λάθος = 0
Βήμα 8: Πύλη XNOR

Η πύλη XNOR είναι αρκετά απλή, είναι βασικά το αντίθετο της πύλης XOR, αυτό σημαίνει ότι το λογικό τεστ είναι επίσης το αντίθετο. Αυτή η πύλη δίνει μια True έξοδο μόνο εάν και οι δύο είσοδοι είναι ο ίδιος αριθμός, με άλλα λόγια κάθε μεικτό σύνολο εισόδων είναι False. Η λογική δοκιμή για την πύλη XOR είναι: Είσοδος1 + Είσοδος2 = 1, αλλά η λογική δοκιμή για την πύλη XNOR είναι: Εισαγωγή1 + Είσοδος2 ≠ 1. (είναι ≠ σε τύπους Excel).
0 + 0 = 0, 0 ≠ 1 τόσο αληθινό = 1
0 + 1 = 1, 1 = 1 τόσο Λάθος = 0
1 + 0 = 1, 1 = 1 τόσο Λάθος = 0
1 + 1 = 2, 2 ≠ 1 τόσο αληθινό = 1
Βήμα 9: ΟΧΙ Πύλη

Η πύλη NOT είναι μια απλή πύλη, αλλά η δήλωση "Εάν" της είναι ίδια με άλλες. Έχει μόνο μία είσοδο, οπότε μπορεί να θέλετε να αλλάξετε τη μορφή σας. Η πύλη αντιστρέφει την είσοδό της, οπότε ο τύπος δεν είναι τόσο σκληρός, η λογική δοκιμή είναι: εάν η είσοδος είναι 0 και η εντολή True είναι: οθόνη 1 αλλιώς εμφάνιση 0.
0 = 0, άρα True = 1
1 ≠ 0, άρα Λάθος = 0
Βήμα 10: Digitalηφιακό κύκλωμα λογικής

Αφού δημιουργήσετε όλες τις λογικές πύλες, μπορείτε να τις χρησιμοποιήσετε για να δημιουργήσετε λογικά κυκλώματα στο Excel. Αλλά η τρέχουσα μορφή είναι πολύ μεγάλη, ώστε να μπορείτε να δοκιμάσετε τη νέα μορφή (εικόνα παραπάνω).
Δημιουργήστε δύο στήλες πλάτους ενός ψηφίου, συγχωνεύστε δύο επάνω κελιά για να δημιουργήσετε οθόνη εξόδου, ενώ τα δύο κάτω κελιά είναι είσοδοι.
Όταν πληκτρολογείτε τον τύπο, πληκτρολογήστε τον τύπο της πύλης που θέλετε στη θέση εμφάνισης εξόδου.
Βήμα 11: Αντιμετώπιση προβλημάτων
Εάν σε οποιοδήποτε στάδιο μια λογική πύλη δεν λειτουργεί σωστά, βεβαιωθείτε ότι ο τύπος που έχετε πληκτρολογήσει σωστά και ότι οι είσοδοι είναι σωστά συνδεδεμένοι με τον τύπο.
Εάν είστε βέβαιοι ότι όλα είναι σωστά, τότε ίσως έκανα λάθος γράφοντας αυτό το διδακτικό, αν ναι, πείτε μου στα σχόλια για να διορθώσω.
Συνιστάται:
Δημιουργήστε όμορφα σχέδια από ζωντανά δεδομένα Arduino (και αποθηκεύστε τα δεδομένα στο Excel): 3 βήματα
Δημιουργήστε όμορφα σχέδια από ζωντανά δεδομένα Arduino (και αποθηκεύστε τα δεδομένα στο Excel): Σε όλους μας αρέσει να παίζουμε με τη λειτουργία P … lotter στο Arduino IDE. Ωστόσο, ενώ μπορεί να είναι χρήσιμο για βασικές εφαρμογές, τα δεδομένα διαγράφονται όσο περισσότερο προστίθενται σημεία και δεν είναι ιδιαίτερα ευχάριστο στα μάτια. Ο σχεδιαστής Arduino IDE δεν
Σύνολο προϊόντων κυκλώματος χρησιμοποιώντας τις λογικές πύλες: 4 βήματα
Κύκλος προϊόντων συνολικού κύκλου χρησιμοποιώντας λογικές πύλες: Σε αυτό το διδακτικό, θα σας δείξω πώς να δημιουργήσετε το δικό σας σύστημα χρησιμοποιώντας το άθροισμα των προϊόντων, λίγη Boolean άλγεβρα και μερικές λογικές πύλες. Δεν χρειάζεται να δημιουργήσετε το ίδιο ακριβές σύστημα με αυτό σε αυτό το σεμινάριο, αλλά μπορείτε να χρησιμοποιήσετε
Πύλες διπλού λογικού τρανζίστορ: 10 βήματα
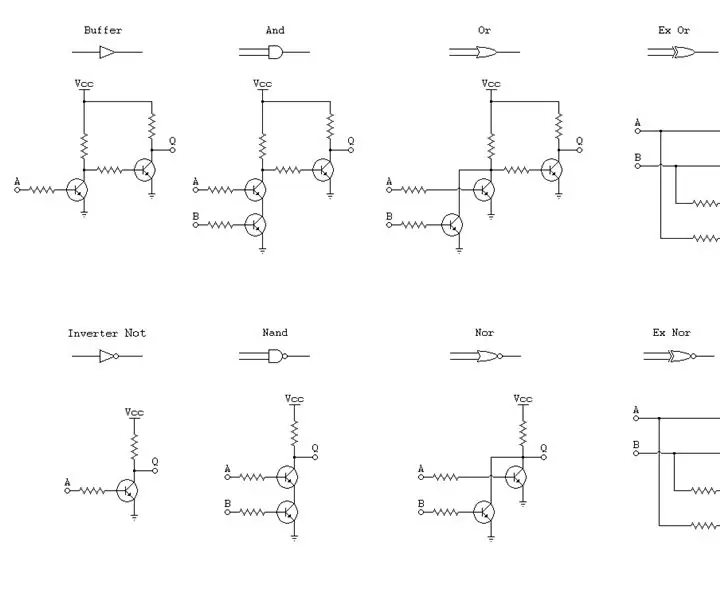
Dual Logic Transistor Gates: Κατασκευάζω πύλες τρανζίστορ λίγο διαφορετικές από τους περισσότερους μηχανικούς ηλεκτρονικών. Οι περισσότεροι άνθρωποι όταν κατασκευάζουν πύλες τρανζίστορ. χτίστε τα με γνώμονα μόνο τη θετική λογική, ωστόσο οι πύλες στα IC έχουν δύο λογικές, τη θετική και την αρνητική λογική. ΕΝΑ
Φτηνές πύλες FPV Drone: 5 βήματα

Φτηνές πύλες FPV Drone: Για όποιον έχει εμπειρία στον αγώνα FPV Drone (Quadcopter), θα καταλάβετε την απογοήτευση για την τιμή των Drone Gates. Αυτές οι πύλες μπορούν να κυμαίνονται από $ 40 η κάθε μία και πάνω. Αποφάσισα να βελτιώσω ένα σχέδιο που έκανε ο Joshua Bardwell (https://www.youtube.com
Δημιουργήστε δυναμικά σχήματα στο Excel με μεταβλητό περιεχόμενο: 4 βήματα

Δημιουργήστε δυναμικά σχήματα στο Excel με μεταβλητό περιεχόμενο: Μπορούμε να χρησιμοποιήσουμε τα σχήματα και τα σχέδια excel με δυναμικό τρόπο για να κάνουμε τα φύλλα εργασίας πιο επαγγελματικά, διαδραστικά και ελκυστικά. Το περιεχόμενο των σχημάτων (το κείμενο γραμμένο σε σχήμα) μπορεί να συνδεθεί με ένα κυτταρικό περιεχόμενο, άρα ένα σχήμα με μεταβλητό κείμενο
