☠WEEDINATOR☠ Μέρος 4: Γεωμετρία διαφορικής διεύθυνσης Κωδικός: 3 βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:37

Εάν έχετε το χρόνο να παρακολουθήσετε το παραπάνω βίντεο, θα παρατηρήσετε ότι υπάρχουν κάποιοι παράξενοι θόρυβοι που προκαλούνται από τους κινητήρες στο τιμόνι που σταματούν κάθε τόσο, καθώς ο WEEDINATOR περιηγείται σε 3 στροφές. Οι κινητήρες μπλέκονται ουσιαστικά μεταξύ τους καθώς η ακτίνα στροφής είναι διαφορετική εσωτερικά προς τα έξω και η απόσταση που διανύει ο τροχός είναι διαφορετική ανά βαθμό στροφής.

Η γεωμετρία της στροφής μπορεί να επεξεργαστεί σκιαγραφώντας 8 περίπου μεταθέσεις της στροφής, δίνοντας παραδείγματα στροφών σε διαφορετικές γωνίες στον εσωτερικό τροχό από 0 (χωρίς στροφή) έως 90 (πλήρες κλείδωμα) μοίρες. Ακούγεται περίπλοκο;

Τα περισσότερα ρομπότ μικρών τροχών δεν προσπαθούν να έχουν κάθε είδους εξελιγμένο σύστημα διεύθυνσης και βασίζονται, πολύ αποτελεσματικά, στην απλή αλλαγή της σχετικής ταχύτητας των κινητήρων σε κάθε πλευρά του οχήματος, η οποία είναι σχεδόν η ίδια με τον τρόπο με τον εντοπισμένο σκαπτικό ή δεξαμενή έργα. Αυτό είναι υπέροχο εάν φορτίζετε σε εμπόλεμη ζώνη γεμάτη κρατήρες και πυροβολείτε ό, τι κινείται, αλλά σε ένα ήσυχο αγροτικό περιβάλλον είναι σημαντικό να κάνετε όσο το δυνατόν λιγότερη ζημιά στο έδαφος και το έδαφος, έτσι ώστε οι τροχοί λείανσης προς τα εμπρός και προς τα εμπρός να είναι μεταξύ τους δεν ενδείκνυται!

Τα περισσότερα αυτοκίνητα και τρακτέρ διαθέτουν ένα πολύ χρήσιμο gadget που ονομάζεται «Διαφορικό», εκτός από τα αυτοκίνητα που βλέπετε σε παλιές αμερικανικές ταινίες όπου μπορείτε να ακούτε τα ελαστικά να τρίζουν σαν τρελά κάθε φορά που πηγαίνουν σε μια στροφή. Οι Αμερικανοί εξακολουθούν να κατασκευάζουν τέτοια αυτοκίνητα; Με το WEEDINATOR, μπορούμε να προγραμματίσουμε διαφορικό στους κινητήριους κινητήρες επεξεργάζοντας τον τύπο για τις σχετικές ταχύτητες και γωνίες των τροχών σε οποιαδήποτε συγκεκριμένη γωνία στροφής. Ακούγεται ακόμα περίπλοκο;

Εδώ είναι ένα γρήγορο παράδειγμα:

Εάν ο WEEDINATOR κινείται σε μια στροφή και έχει τον εσωτερικό του τροχό σε 45 μοίρες, ο εξωτερικός τροχός ΔΕΝ είναι 45 μοίρες, μοιάζει περισσότερο με 30 μοίρες. Επίσης, ο εσωτερικός τροχός μπορεί να περιστρέφεται με 1 χλμ./Ώρα, αλλά ο εξωτερικός τροχός θα είναι σημαντικά πιο γρήγορος, περισσότερο από 1,35 χλμ./Ώρα.

Βήμα 1: Ρύθμιση γεωμετρίας

Μερικές βασικές παραδοχές γίνονται για να ξεκινήσουν με:

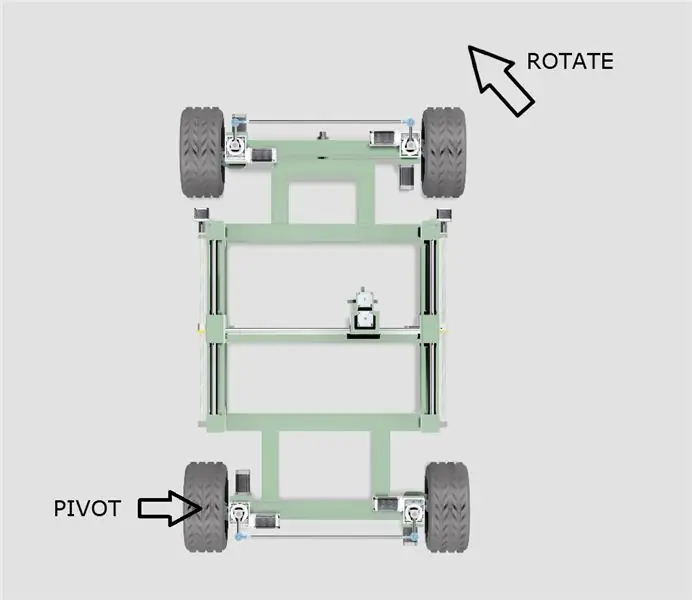
• Το πλαίσιο θα περιστραφεί σε έναν από τους πίσω τροχούς, όπως φαίνεται στο παραπάνω διάγραμμα.
• Το αποτελεσματικό κέντρο του περιστροφικού κύκλου θα κινείται κατά μήκος μιας γραμμής που εκτείνεται από τα κέντρα των δύο πίσω τροχών, ανάλογα με τη γωνία στροφής.
• Η γεωμετρία θα έχει τη μορφή καμπύλης ημιτόνου.

Βήμα 2: Κλιμακωτά σχέδια γωνιών τροχών και ακτίνων

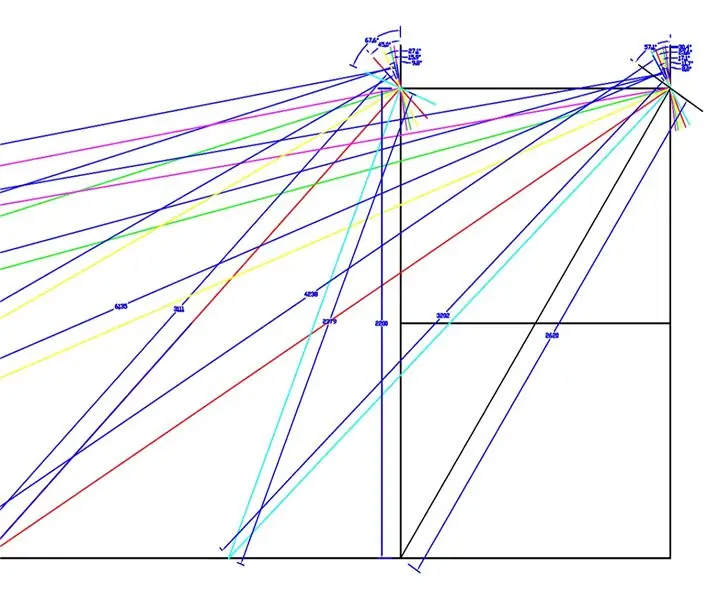
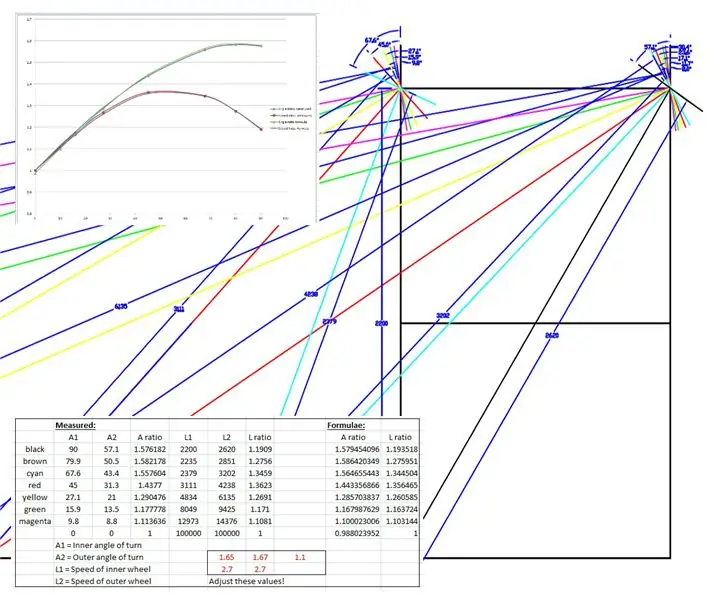
Πραγματοποιήθηκε ένα σχέδιο πλήρους κλίμακας των εμπρός τροχών και του πλαισίου WEEDINATOR με 8 διαφορετικές μεταθέσεις γωνίας εσωτερικού τροχού μεταξύ 0 και 90 μοιρών και τα αντίστοιχα κέντρα στροφής χαρτογραφήθηκαν όπως φαίνεται στα παραπάνω σχέδια.

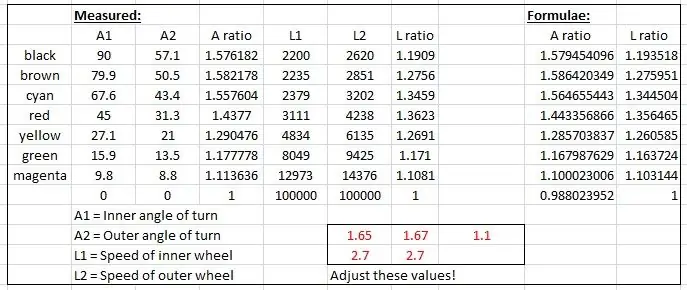
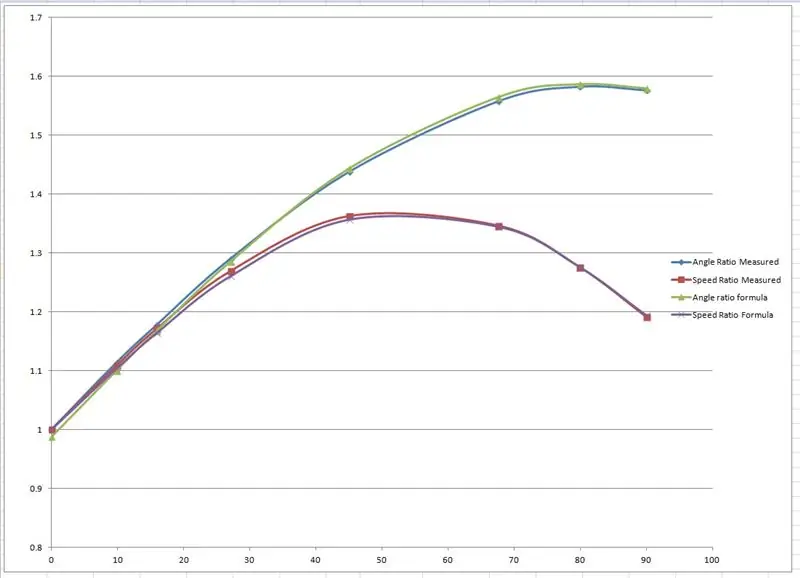
Οι αποτελεσματικές ακτίνες μετρήθηκαν από το σχέδιο και σχεδιάστηκαν σε ένα γράφημα στο Microsoft Excel.

Δημιουργήθηκαν δύο γραφήματα, ένα του λόγου του αριστερού και του δεξιού άξονα του μπροστινού τροχού και ένα άλλο για την αναλογία των δύο ακτίνων για κάθε συγκεκριμένη γωνία στροφής.

Στη συνέχεια, «χτύπησα» κάποιους τύπους για να μιμηθώ τα εμπειρικά αποτελέσματα με βάση μια ημιτονοειδή καμπύλη. Μία από τις φασαρίες μοιάζει με αυτό:

speedRatio = (αμαρτία (εσωτερικό*1.65*pi/180) +2.7) /2.7; // εσωτερική είναι η εσωτερική γωνία στροφής.

Οι καμπύλες παραμορφώθηκαν αλλάζοντας τις τιμές που εμφανίζονται με κόκκινο χρώμα στο αρχείο excel μέχρι να προσαρμοστούν οι καμπύλες.

Βήμα 3: Κωδικοποίηση των τύπων

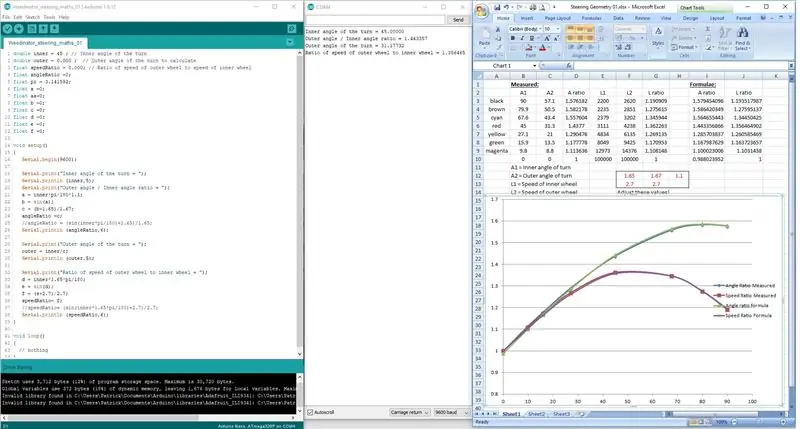
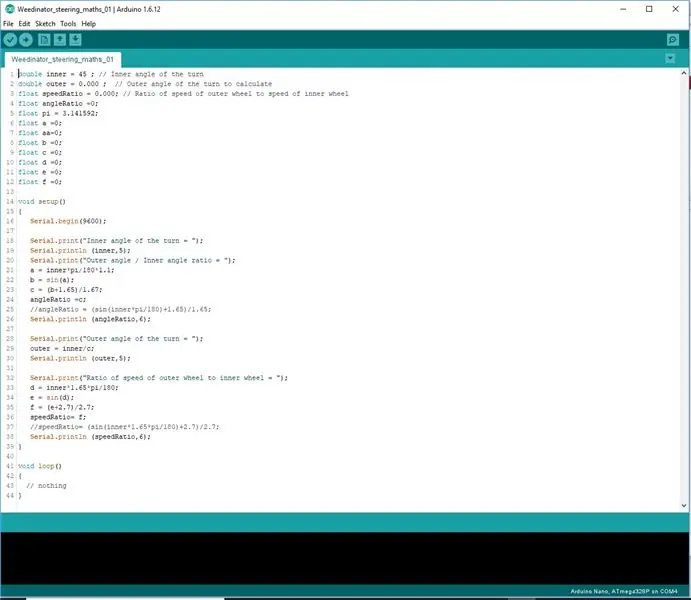
Αντί να προσπαθούν να κωδικοποιήσουν τους τύπους σε μία γραμμή, χωρίστηκαν σε 3 στάδια για να επιτρέψουν στο Arduino να επεξεργαστεί σωστά τα μαθηματικά.

Τα αποτελέσματα εμφανίζονται στην οθόνη σειριακής θύρας και ελέγχονται με τα μετρημένα αποτελέσματα στο σχέδιο κλίμακας.