Χρησιμοποιήστε 1 αναλογική είσοδο για 6 κουμπιά για Arduino: 6 βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:36

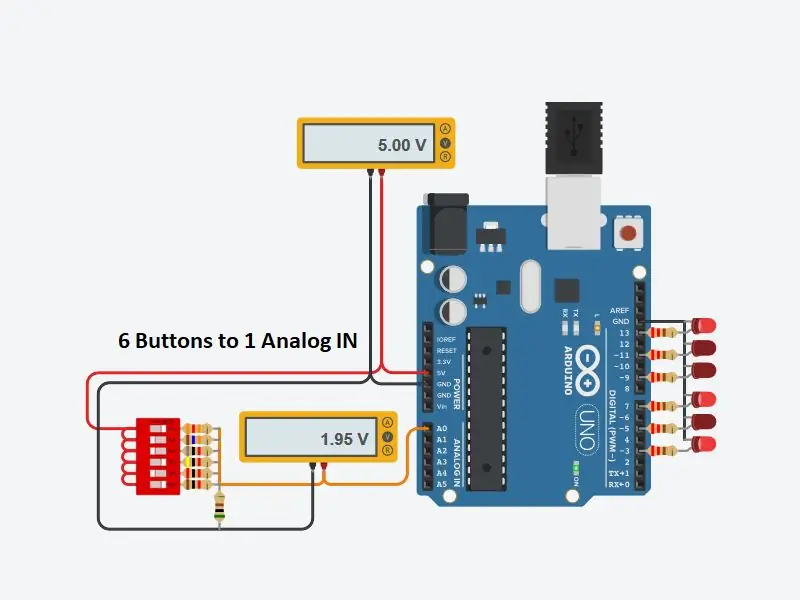
Έχω αναρωτηθεί συχνά πώς θα μπορούσα να λάβω περισσότερες ψηφιακές εισόδους για το Arduino μου. Πρόσφατα μου ήρθε στο μυαλό ότι θα έπρεπε να μπορώ να χρησιμοποιήσω μία από τις Αναλογικές Εισόδους για την εισαγωγή πολλαπλών ψηφιακών εισόδων. Έκανα μια γρήγορη αναζήτηση και βρήκα πού ήταν σε θέση να το κάνουν οι άνθρωποι, αλλά αυτό επέτρεπε να πατηθεί μόνο ένα κουμπί κάθε φορά. Θέλω να μπορώ να έχω οποιοδήποτε συνδυασμό κουμπιών για να πατηθεί ΑΥΤΟΜΑΤΑ. Έτσι, με τη βοήθεια των TINKERCAD CIRCUITS, ξεκίνησα να το κάνω αυτό πραγματικότητα.

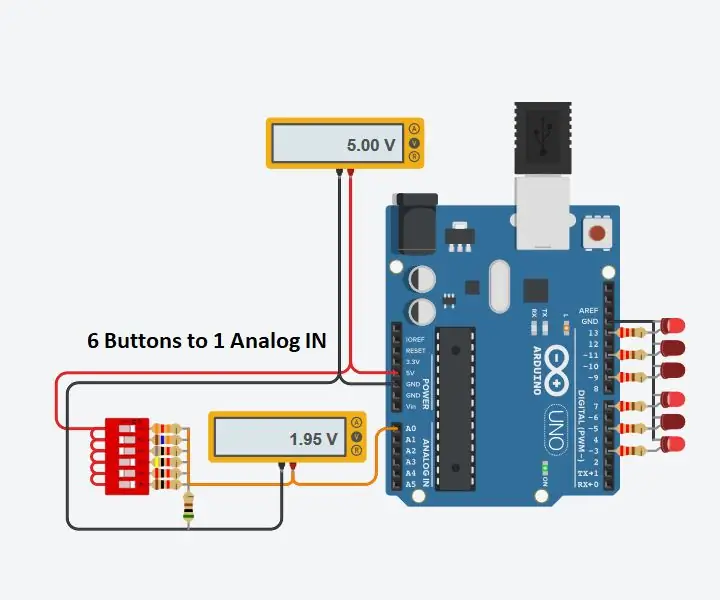
Γιατί θα ήθελα ταυτόχρονες πιέσεις κουμπιών; Όπως απεικονίζεται στο σχεδιασμό των κυκλωμάτων TinkerCad, θα μπορούσε να χρησιμοποιηθεί για εισόδους διακόπτη DIP για επιλογή διαφορετικών τρόπων λειτουργίας μέσα στο πρόγραμμα.

Το κύκλωμα που βρήκα χρησιμοποιεί την πηγή 5V που είναι διαθέσιμη από το Arduino και χρησιμοποιεί 7 αντιστάσεις και 6 κουμπιά ή διακόπτες.

Βήμα 1: Το κύκλωμα

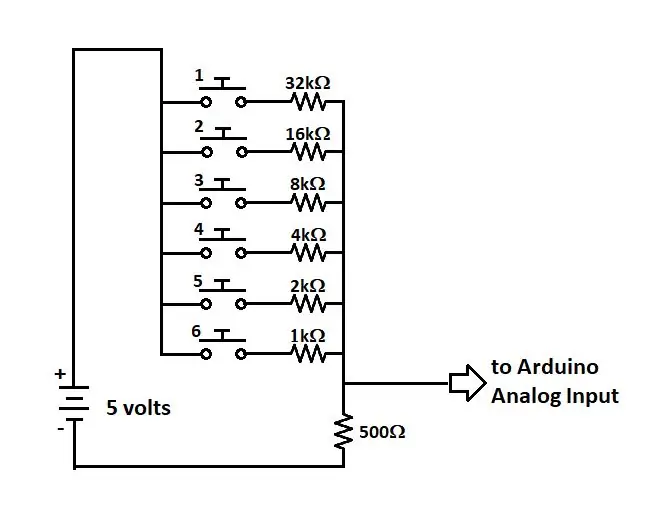
Τα Arduino έχουν αναλογικές εισόδους που δέχονται είσοδο 0V έως 5V. Αυτή η είσοδος έχει ανάλυση 10-bit, που σημαίνει ότι το σήμα διασπάται σε 2^10 τμήματα ή 1024 μετρήσεις. Με βάση αυτό, το μέγιστο που θα μπορούσαμε ποτέ να εισάγουμε σε μια αναλογική είσοδο, ενώ επιτρέπουμε ταυτόχρονες πιέσεις θα ήταν 10 κουμπιά σε 1 αναλογική είσοδος. Αλλά, αυτός δεν είναι ένας τέλειος κόσμος. Υπάρχει αντίσταση στους αγωγούς, θόρυβο από εξωτερικές πηγές και ατελής ισχύ. Έτσι, για να έχω αρκετή ευελιξία, σχεδίασα να το σχεδιάσω για 6 κουμπιά. Αυτό, εν μέρει, επηρεάστηκε από το γεγονός ότι τα κυκλώματα TinkerCAD διέθεταν ένα αντικείμενο διακόπτη 6 διακόπτη, το οποίο θα έκανε τον έλεγχο εύκολο.

Το πρώτο βήμα στο σχεδιασμό μου ήταν να βεβαιωθώ ότι κάθε κουμπί, όταν πατηθεί ξεχωριστά, θα παρέχει μια μοναδική τάση. Αυτό αποκλείει όλες τις αντιστάσεις να έχουν την ίδια τιμή. Το επόμενο βήμα ήταν ότι οι τιμές αντίστασης, όταν προστεθούν παράλληλα, δεν θα μπορούσαν να έχουν την ίδια αντίσταση με οποιαδήποτε τιμή αντίστασης. Όταν οι αντιστάσεις συνδέονται παράλληλα, η προκύπτουσα αντίσταση μπορεί να υπολογιστεί με Rx = 1/[(1/R1)+(1/R2)]. Έτσι, αν R1 = 2000 και R2 = 1000, Rx = 667. Υποθέτω ότι διπλασιάζοντας το μέγεθος κάθε αντίστασης, δεν θα έβλεπα την ίδια αντίσταση για κανέναν από τους συνδυασμούς.

Έτσι, το κύκλωμά μου σε αυτό το σημείο ήταν να έχω 6 διακόπτες, ο καθένας με τη δική του αντίσταση. Όμως, απαιτείται ακόμη μία αντίσταση για να ολοκληρωθεί αυτό το κύκλωμα.

Η τελευταία αντίσταση έχει 3 σκοπούς. Πρώτον, λειτουργεί ως αντίσταση Pull-Down. Χωρίς την αντίσταση, όταν δεν πατήσετε κανένα κουμπί, το κύκλωμα είναι ελλιπές. Αυτό θα επέτρεπε στην τάση στην αναλογική είσοδο του Arduino να επιπλέει σε οποιοδήποτε δυναμικό τάσης. Μια αντίσταση Pull-Down ουσιαστικά κατεβάζει την τάση στα 0 V. Ο δεύτερος σκοπός είναι να περιοριστεί το ρεύμα αυτού του κυκλώματος. Ο νόμος του Ohm δηλώνει ότι V = IR, ή Voltage = ρεύμα πολλαπλασιασμένο με αντίσταση. Με μια δεδομένη πηγή τάσης, όσο μεγαλύτερη είναι η αντίσταση σημαίνει ότι το ρεύμα θα είναι μικρότερο. Έτσι, εάν εφαρμοζόταν ένα σήμα 5V σε αντίσταση 500ohm, το μεγαλύτερο ρεύμα που θα μπορούσαμε να δούμε θα ήταν 0,01Α, ή 10mA. Ο τρίτος σκοπός είναι η παροχή τάσης σήματος. Το συνολικό ρεύμα που διαρρέει την τελευταία αντίσταση θα είναι: i = 5V/Rtotal, όπου Rtotal = Rlast+{1/[(1/R1)+(1/R2)+(1/R3)+(1/R4)+ (1/R5)+(1/R6)]}. Ωστόσο, συμπεριλάβετε μόνο 1/Rx για κάθε αντίσταση που έχει πατήσει το αντίστοιχο κουμπί. Από το συνολικό ρεύμα, η Τάση που παρέχεται στην Αναλογική Είσοδο θα ήταν i*Rlast, ή i*500.

Βήμα 2: Απόδειξη - Excel

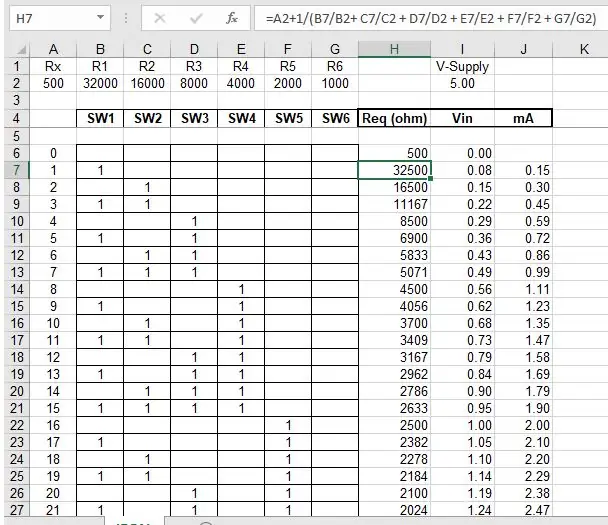
Ο γρηγορότερος και ευκολότερος τρόπος για να αποδείξω ότι θα έχω μοναδικές αντιστάσεις και συνεπώς μοναδικές τάσεις με αυτό το κύκλωμα ήταν να χρησιμοποιήσω τις δυνατότητες του Excel.

Δημιούργησα όλους τους πιθανούς συνδυασμούς εισόδων διακόπτη και οργάνωσα αυτά τα διαδοχικά ακολουθώντας δυαδικά μοτίβα. Μια τιμή "1" υποδεικνύει ότι ο διακόπτης είναι ενεργοποιημένος, το κενό δείχνει ότι είναι απενεργοποιημένος. Στο επάνω μέρος του υπολογιστικού φύλλου, έβαλα τις τιμές αντίστασης για κάθε διακόπτη και για την αντίσταση αναδίπλωσης. Στη συνέχεια, υπολόγισα την ισοδύναμη αντίσταση για καθέναν από τους συνδυασμούς, εκτός από τις περιπτώσεις που όλες οι αντιστάσεις είναι απενεργοποιημένες, καθώς αυτές οι αντιστάσεις δεν θα επηρεάσουν χωρίς να την τροφοδοτήσει μια πηγή ισχύος. Για να κάνω τους υπολογισμούς μου εύκολους ώστε να μπορώ να αντιγράψω και να επικολλήσω σε κάθε συνδυασμό, συμπεριέλαβα όλους τους συνδυασμούς στον υπολογισμό πολλαπλασιάζοντας κάθε τιμή διακόπτη (0 ή 1) με την αντίστροφη τιμή αντίστασης. Με αυτόν τον τρόπο εξαλείφεται η αντίστασή του από τον υπολογισμό εάν ο διακόπτης ήταν κλειστός. Η εξίσωση που προκύπτει μπορεί να φανεί στην εικόνα του υπολογιστικού φύλλου, αλλά Req = Rx + 1/(Sw1/R1 + Sw2/R2 + Sw3/R3 + Sw4/R4 + Sw5/R5 + Sw6/R6). Χρησιμοποιώντας το Itotal = 5V / Req, καθορίζουμε το συνολικό ρεύμα μέσω του κυκλώματος. Αυτό είναι το ίδιο ρεύμα που περνάει από την αντίσταση Pull-down και μας παρέχει την Τάση στην Αναλογική Είσοδό μας. Αυτό υπολογίζεται ως Vin = Itotal x Rx. Εξετάζοντας τόσο τα δεδομένα Req όσο και τα δεδομένα Vin, μπορούμε να δούμε ότι πράγματι έχουμε μοναδικές τιμές.

Σε αυτό το σημείο, φαίνεται ότι το κύκλωμά μας θα λειτουργήσει. Τώρα για να καταλάβετε πώς να προγραμματίσετε το Arduino.

Βήμα 3: Προγραμματισμός Arduino

Όταν άρχισα να σκέφτομαι πώς να προγραμματίσω το Arduino, αρχικά σχεδίασα τη ρύθμιση μεμονωμένων περιοχών τάσης για να καθορίσω αν ο διακόπτης ήταν ενεργοποιημένος ή απενεργοποιημένος. Όμως, ενώ ήμουν ξαπλωμένος στο κρεβάτι ένα βράδυ, μου ήρθε στο μυαλό ότι θα έπρεπε να είμαι σε θέση να βρω μια εξίσωση για να το κάνω αυτό. Πως? ΠΡΟΕΧΩ. Το Excel έχει τη δυνατότητα να υπολογίζει τις εξισώσεις για την καλύτερη προσαρμογή δεδομένων σε ένα γράφημα. Για να γίνει αυτό, θα ήθελα μια εξίσωση της Ακέραιας τιμής των διακοπτών (δυαδικό) έναντι της εισόδου τάσης που αντιστοιχεί σε αυτήν την τιμή. Στο βιβλίο εργασίας του Excel, έβαλα την Ακεραία τιμή στην αριστερή πλευρά του υπολογιστικού φύλλου. Τώρα για να καθορίσω την εξίσωση μου.

Ακολουθεί ένα γρήγορο σεμινάριο για τον τρόπο προσδιορισμού της εξίσωσης μιας γραμμής στο Excel.

1) Επιλέξτε ένα κελί που δεν περιέχει δεδομένα. Εάν έχετε επιλέξει ένα κελί που έχει δεδομένα, το Excel θα προσπαθήσει να μαντέψει τι θέλετε να κάνετε. Αυτό καθιστά πολύ πιο δύσκολο να δημιουργηθεί μια τάση, επειδή το Excel σπάνια προβλέπει σωστά.

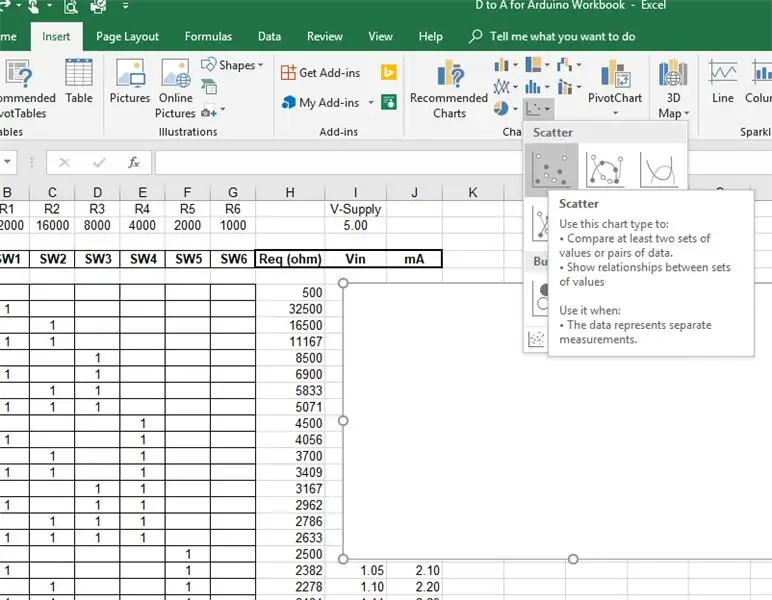
2) Επιλέξτε την καρτέλα "Εισαγωγή" και επιλέξτε ένα γράφημα "Scatter".

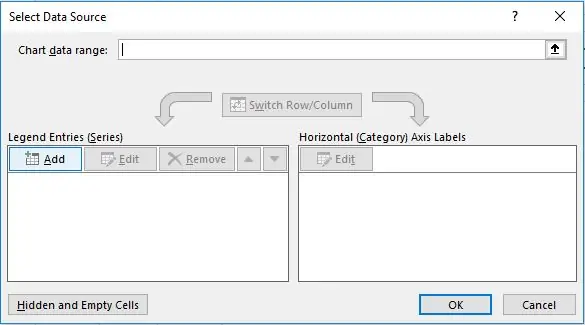
3) Κάντε δεξί κλικ στο πλαίσιο γραφήματος και κάντε κλικ στο "Επιλογή δεδομένων …". Θα εμφανιστεί το παράθυρο "Επιλογή πηγής δεδομένων". Επιλέξτε το κουμπί Προσθήκη για να συνεχίσετε να επιλέγετε τα δεδομένα.

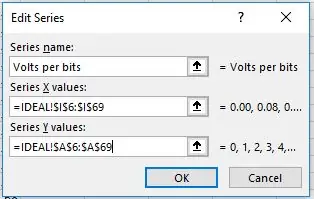
4) Δώστε ένα όνομα σειράς (προαιρετικό). Επιλέξτε το εύρος για τον άξονα Χ κάνοντας κλικ στο επάνω βέλος και, στη συνέχεια, επιλέγοντας τα δεδομένα τάσης. Επιλέξτε το εύρος για τον άξονα Υ κάνοντας κλικ στο επάνω βέλος και, στη συνέχεια, επιλέγοντας τα ακέραια δεδομένα (0-63).

5) Κάντε δεξί κλικ στα σημεία δεδομένων και επιλέξτε "Προσθήκη γραμμής τάσης …" Στο παράθυρο "Μορφοποίηση γραμμής τάσης", επιλέξτε το κουμπί Πολυωνυμικό. Κοιτάζοντας την τάση, βλέπουμε ότι το Order of 2 δεν ταιριάζει απόλυτα. Επέλεξα μια παραγγελία 3 και θεώρησα ότι αυτό ήταν πολύ πιο ακριβές. Επιλέξτε το πλαίσιο ελέγχου για "Εξίσωση εμφάνισης στο γράφημα". Η τελική εξίσωση τώρα εμφανίζεται στο γράφημα.

6) Έγινε.

ΕΝΤΑΞΕΙ. Επιστροφή στο πρόγραμμα Arduino. Τώρα που έχουμε την εξίσωση, ο προγραμματισμός του Arduino είναι εύκολος. Ο ακέραιος αριθμός που αντιπροσωπεύει τις θέσεις του διακόπτη υπολογίζεται σε 1 γραμμή κωδικού. Χρησιμοποιώντας τη συνάρτηση "bitread", μπορούμε να πιάσουμε την τιμή κάθε μεμονωμένου bit και έτσι να γνωρίζουμε την κατάσταση κάθε κουμπιού. (ΔΕΙΤΕ ΦΩΤΟΓΡΑΦΙΕΣ)

Βήμα 4: Κυκλώματα TinkerCAD

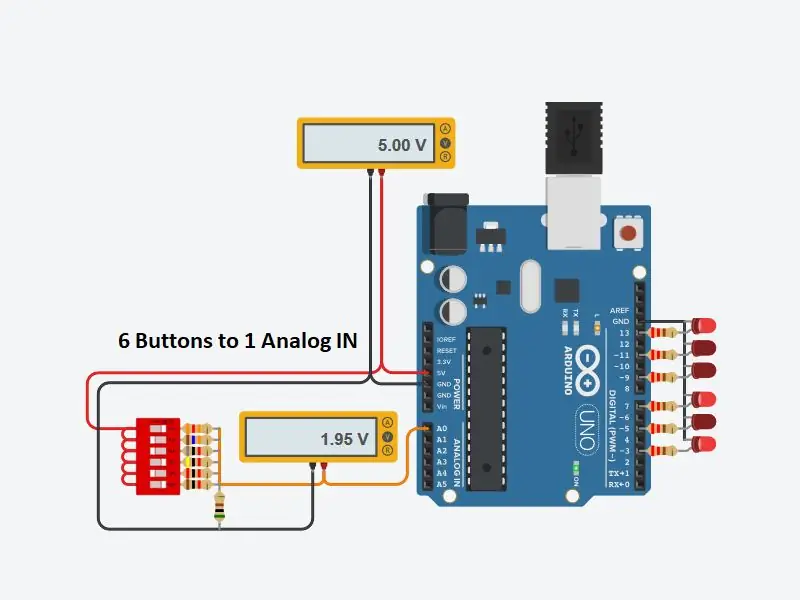
Εάν δεν έχετε ελέγξει τα κυκλώματα TinkerCAD, κάντε το τώρα. ΠΕΡΙΜΕΝΕ!!!! Τελειώστε την ανάγνωση του Instructable μου και, στη συνέχεια, ελέγξτε το. Τα κυκλώματα TinkerCAD καθιστούν τη δοκιμή κυκλωμάτων Arduino πολύ εύκολη. Περιλαμβάνει πολλά ηλεκτρικά αντικείμενα και Arduinos, επιτρέποντάς σας ακόμη και να προγραμματίσετε το Arduino για δοκιμές.

Για να δοκιμάσω το κύκλωμά μου, έστησα 6 διακόπτες χρησιμοποιώντας ένα πακέτο διακόπτη DIP και τους έδεσα στις αντιστάσεις. Για να αποδείξω ότι η τιμή τάσης στο υπολογιστικό φύλλο του Excel ήταν σωστή, εμφάνισα ένα βολτόμετρο στην είσοδο στο Arduino. Όλα αυτά λειτούργησαν όπως αναμενόταν.

Για να αποδείξω ότι ο προγραμματισμός Arduino λειτούργησε, έβγαλα τις καταστάσεις των διακοπτών σε LED, χρησιμοποιώντας τις ψηφιακές εξόδους του Arduino.

Στη συνέχεια άλλαξα κάθε διακόπτη για κάθε πιθανό συνδυασμό και είμαι περήφανος που λέω "ΛΕΙΤΟΥΡΓΕΙ" !!!

Βήμα 5: "Τόσο καιρό, και ευχαριστώ για όλα τα ψάρια". (αναφορά 1)

Δεν έχω ακόμη δοκιμάσει αυτό με πραγματικό εξοπλισμό, καθώς ταξιδεύω αυτή τη στιγμή για δουλειά. Αλλά, αφού το απέδειξα με τα κυκλώματα TinkerCAD, πιστεύω ότι θα λειτουργήσει. Η πρόκληση είναι ότι οι τιμές των αντιστάσεων που έχω καθορίσει δεν είναι όλες οι τυπικές τιμές για αντιστάσεις. Για να το ξεπεράσω, σκοπεύω να χρησιμοποιήσω ποτενσιόμετρα και συνδυασμούς αντιστάσεων για να πάρω τις τιμές που χρειάζομαι.

Σας ευχαριστώ που διαβάσατε το διδακτικό μου. Ελπίζω να σας βοηθήσει με τα έργα σας.

Παρακαλώ αφήστε σχόλια εάν προσπαθήσατε να αντιμετωπίσετε το ίδιο εμπόδιο και πώς το είχατε λύσει. Θα μου άρεσε να μάθω περισσότερους τρόπους για να το κάνω αυτό.

Βήμα 6: Αναφορές

Δεν νομίζατε ότι θα παράσχω ένα απόσπασμα χωρίς να δώσω μια αναφορά στην πηγή του, έτσι;

αναφορά 1: Άνταμς, Ντάγκλας. Τόσο καιρό, και ευχαριστώ για όλα τα ψάρια. (Το 4ο βιβλίο της «τριλογίας» του Οδηγού των Οστόστορων στον Γαλαξία)