Γνωρίζετε για το ESP32 ADC Adjustment ;: 29 Βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:36

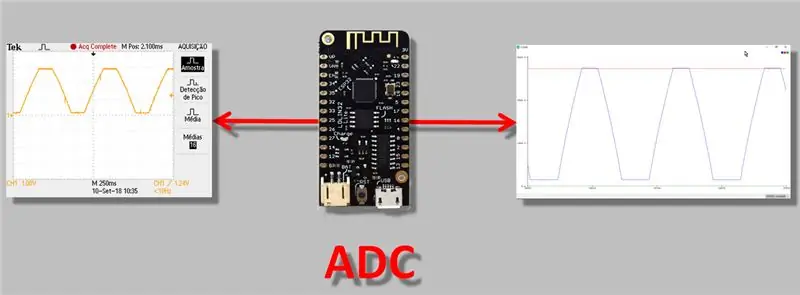
Σήμερα, θα μιλήσω για ένα πιο τεχνικό ζήτημα, αλλά νομίζω ότι όλοι όσοι εργάζονται με το ESP32 πρέπει να γνωρίζουν: το ζήτημα της προσαρμογής ανάγνωσης ADC (μετατροπέας αναλογικού σε ψηφιακό). Το βρίσκω σημαντικό διότι όταν κάνετε μια "μέτρηση", ειδικά με ένα όργανο που έχει αναλογική έξοδο, πρέπει να είστε απολύτως σίγουροι ότι η ανάγνωση εκτελείται σωστά.

Στο βίντεο σήμερα, λοιπόν, θα πραγματοποιήσουμε μετρήσεις χρησιμοποιώντας τον "αναλογικό-ψηφιακό μετατροπέα" του ESP32, θα παρατηρήσουμε τις αποκλίσεις μετατροπής και θα εφαρμόσουμε μια μέθοδο προσαρμογής / βαθμονόμησης ADC.

Βήμα 1: Τι είναι ένας μετατροπέας AD;

Ο μετατροπέας AD είναι ένα κύκλωμα ικανό να μεταφράσει μια αναλογική (συνεχή) ποσότητα σε ψηφιακές (διακριτές) τιμές. Τι σημαίνει αυτό? Αυτό σημαίνει ότι ενώ οι ψηφιακές τιμές μπορούν να υποθέσουν μόνο διακριτές τιμές που σχηματίζονται από το συνδυασμό μηδενικών και μονάδων, μια αναλογική ποσότητα μπορεί να λάβει οποιαδήποτε τιμή εντός ενός εύρους. Για παράδειγμα, αν μετρήσουμε την τάση μιας ιδανικής κυψέλης ΑΑ, θα μπορούσαμε να βρούμε οποιαδήποτε τιμή μεταξύ 0V και 1.5V, αφού πρόκειται για αναλογική ποσότητα. Η κατάσταση εξόδου ενός ιδανικού λαμπτήρα πρέπει να έχει μόνο δύο καταστάσεις (σβηστή ή ενεργοποιημένη), η οποία είναι διακριτό μέγεθος. Δεδομένου ότι οι μικροελεγκτές λειτουργούν χρησιμοποιώντας αυτήν τη διακριτή λογική, χρειαζόμαστε ένα κύκλωμα ικανό να μεταφράσει μια αναλογική ποσότητα σε ψηφιακή (ή διακριτή).

Βήμα 2: Χρησιμοποιημένοι πόροι

• Μια κάρτα Lolin32 Lite v1.0.0

• Ένα παλμογράφο Tektronix TDS1001C για λήψη

• Ένα καλώδιο USB για το ESP32

• Ένας παλμογράφος Hantek DSO4102C ως γεννήτρια σήματος

Βήμα 3: ESP32 ADC

Σύμφωνα με τα δεδομένα του Espressif, τα τσιπ ESP32 μπορεί να παρουσιάζουν διαφορά +/- 6% από το ένα τσιπ στο άλλο στα μετρημένα αποτελέσματα.

Επιπλέον, η μετατροπή ΔΕΝ έχει γραμμική απάντηση για κάθε διαθέσιμο εύρος για ανάγνωση. Το Espressif παρέχει μια μέθοδο βαθμονόμησης και προτείνει στους χρήστες να εφαρμόσουν άλλες μεθόδους εάν το κρίνουν απαραίτητο για να επιτύχουν την επιθυμητή ακρίβεια.

Θα πραγματοποιήσουμε μια απόκτηση δεδομένων και από αυτό, θα δείξουμε τις απαντήσεις ADC και ένα παράδειγμα εφαρμογής μαθηματικής διαδικασίας για την ανάγνωση της προσαρμογής.

Υπάρχουν αρκετοί (απλούστεροι ή πιο σύνθετοι) τρόποι για να επιτευχθούν αυτές οι επιδιορθώσεις. Εναπόκειται σε εσάς να αξιολογήσετε το καταλληλότερο για το έργο σας.

Αυτό που φαίνεται εδώ θα έχει έναν επεξηγηματικό σκοπό και θα προσπαθήσει να αντιμετωπίσει ενδιαφέροντα σημεία που μπορούν να παρατηρηθούν κατά τη διάρκεια των προσαρμογών.

Βήμα 4: Χρησιμοποιείται κύκλωμα

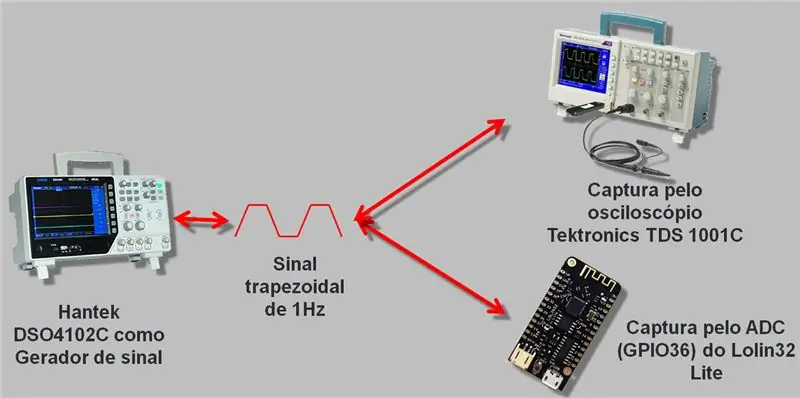
Χρησιμοποίησα έναν παλμογράφο με γεννήτρια σήματος που ανεβαίνει στα 25 MHz, το Hantek DSO4102C. Δημιουργήσαμε ένα κύμα που διαβάστηκε από το ESP A / D και τον παλμογράφο. Τα δεδομένα που συλλέχθηκαν καταγράφηκαν σε csv και σε υπολογιστικό φύλλο, το οποίο θα αφήσω στο τέλος του άρθρου για λήψη.

Βήμα 5: Χρησιμοποιήθηκε η υπογραφή

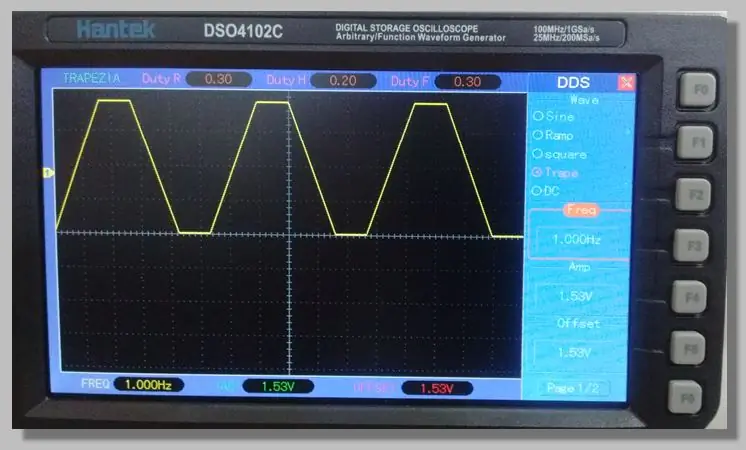
Επιλέξαμε ένα τραπεζοειδές σήμα χαμηλής συχνότητας που επιτρέπει την πρόσβαση στις ράμπες που διατρέχουν όλο το εύρος μετατροπών. Αυτό επιτρέπει μεγάλο αριθμό δειγμάτων σε αυτές τις ράμπες.

Βήμα 6: Δεδομένα που λαμβάνονται από το παλμογράφο

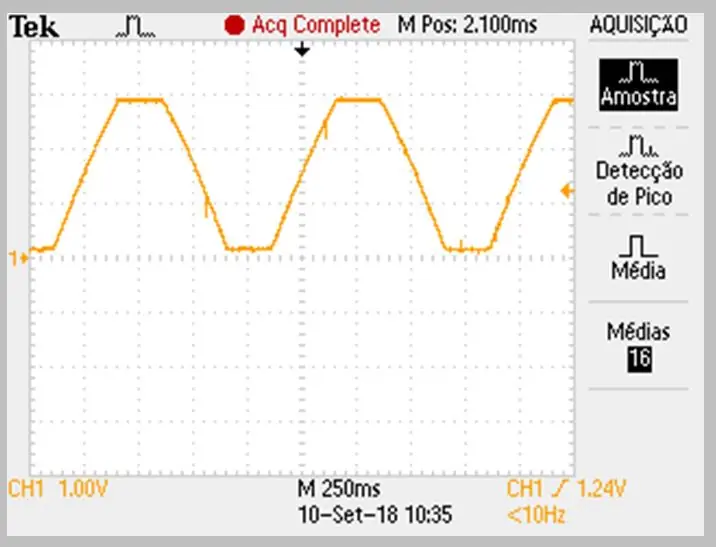
Η εικόνα της λήψης πραγματοποιήθηκε με παλμογράφο. Τα δεδομένα αποθηκεύτηκαν σε ένα αρχείο csv. Σημειώστε την ελαφρά καμπυλότητα στις ανερχόμενες και κατερχόμενες ράμπες του σήματος.

Βήμα 7: Δεδομένα που λαμβάνονται από το παλμογράφο (αρχείο csv στο Excel)

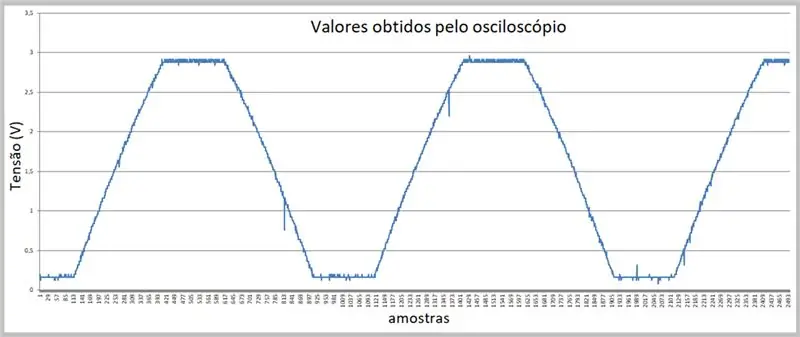
Έχουμε τα δείγματα εδώ.

Βήμα 8: Δεδομένα που λαμβάνονται από το ADC

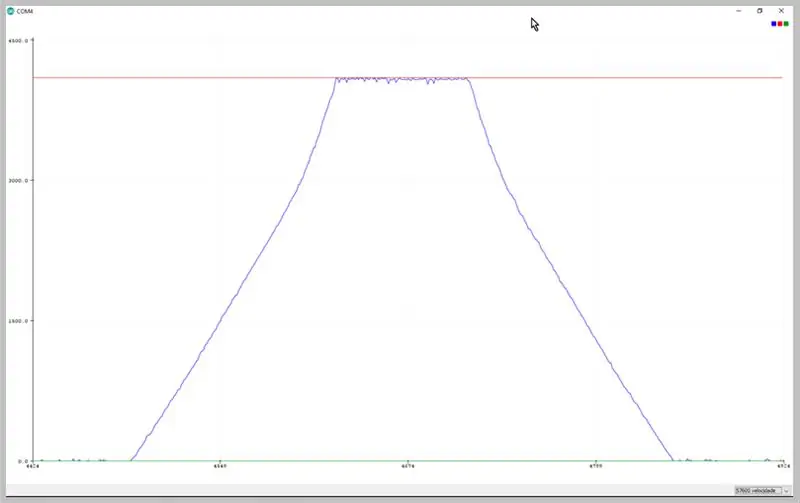
Αλλάζοντας το ρυθμό μεταφοράς του σειριακού, μπορούμε να δούμε τα δεδομένα που συλλέγονται από το ADC. Παρατηρήστε την παραμόρφωση του τραπεζοειδούς σήματος.

Δεδομένα που παρατηρούνται στο σειριακό plotter του Arduino IDE

Βήμα 9: Δεδομένα που λαμβάνονται από το ADC - Excel

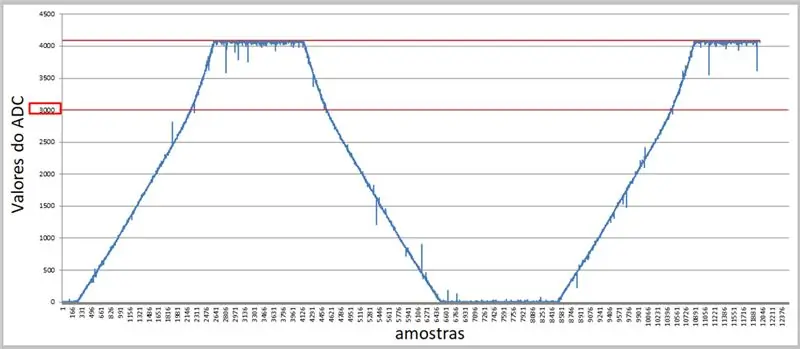
Χρησιμοποιώντας ένα υψηλότερο ποσοστό και το σειριακό τερματικό, μπορούμε να καταγράψουμε τις τιμές και να τις εφαρμόσουμε στο Excel για τις συγκρίσεις μας.

Βήμα 10: Σύγκριση των ράμπων ανάβασης

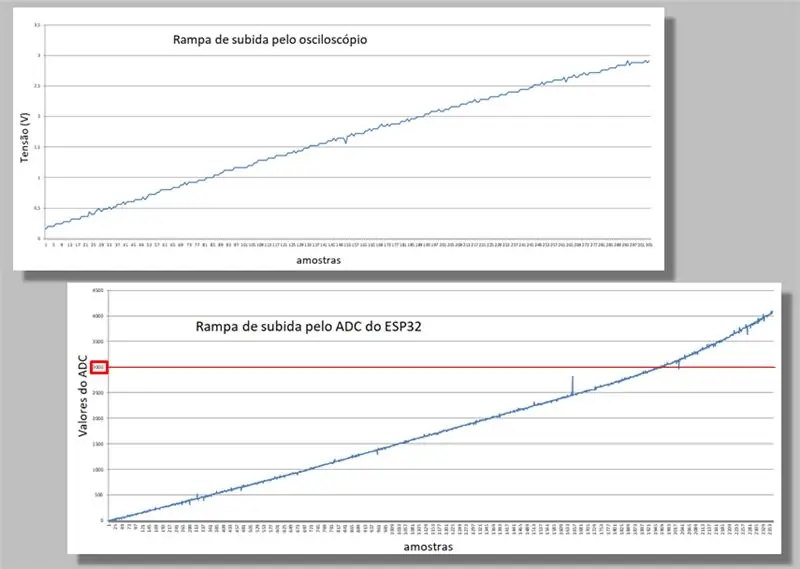
Συγκρίνουμε τις δύο ράμπες αναρρίχησης των δύο αλιευμάτων.

Σημειώστε την καμπυλότητα που συμβαίνει και στις δύο ράμπες.

Σημειώστε επίσης ότι για την ίδια ράμπα, έχουμε πολλά περισσότερα δείγματα του ESP32 παρά από τον παλμογράφο.

Βήμα 11: Εξίσωση του αριθμού των δειγμάτων

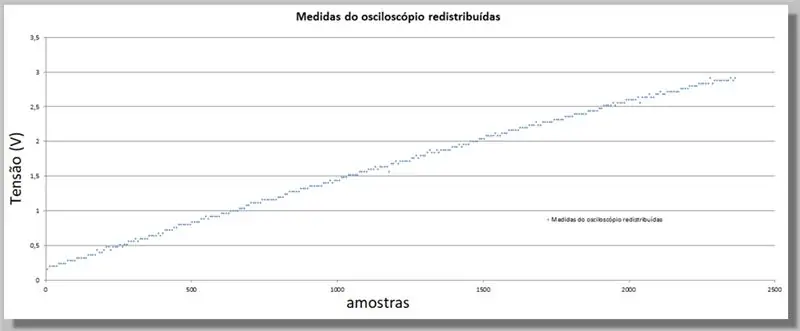
Επειδή το ESP32 παρείχε μεγαλύτερο αριθμό δειγμάτων από το παλμογράφο, πρέπει να εξισώσουμε αυτές τις τιμές, καθώς θα χρησιμεύσουν ως δείκτης για τη σύγκριση των δύο καμπυλών.

Για αυτό, θα κάνουμε μια άμεση σύγκριση.

Έχουμε 305 δείγματα για ράμπα παλμογράφου και 2365 δείγματα για ράμπα ADC.

Δεδομένου ότι οι ράμπες είναι του ίδιου εύρους, μπορούμε να πούμε ότι έχουμε περίπου 7,75 δείγματα του ADC για κάθε παλμογράφο.

Ο πολλαπλασιασμός του δείκτη κάθε δείγματος παλμογράφου έχει την ίδια καμπύλη, αλλά με δείκτες ισοδύναμους με τον ADC και τα αναδιανεμημένα δεδομένα.

Για να συμπληρώσουμε τα δεδομένα που λείπουν για τις νέες θέσεις, θα εφαρμόσουμε μια καμπύλη που ταιριάζει στατιστικά με τα γνωστά δεδομένα.

Βήμα 12: Συμπλήρωση των κενών - γραμμή τάσης

Επιλέγοντας τα γνωστά δεδομένα (μπλε κουκκίδες), κάνοντας κλικ και έπειτα κάνοντας κλικ με το δεξί κουμπί, επιλέγουμε: "Προσθήκη γραμμής τάσης …"

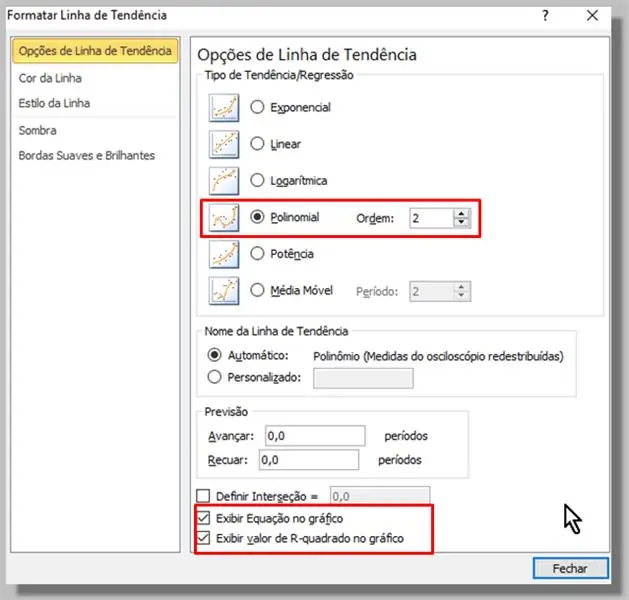
Στο παράθυρο που εμφανίζεται, επιλέγουμε τον τύπο Πολυωνυμίας (η σειρά 2 θα είναι αρκετή).

Ελέγξαμε επίσης τις επιλογές "Προβολή εξίσωσης στο γράφημα" και "Εμφάνιση τιμής τετραγώνου R στο γράφημα".

Κάνουμε κλικ στο "Κλείσιμο".

Βήμα 13: Συμπλήρωση κενών - πολυωνυμική καμπύλη βαθμού 2

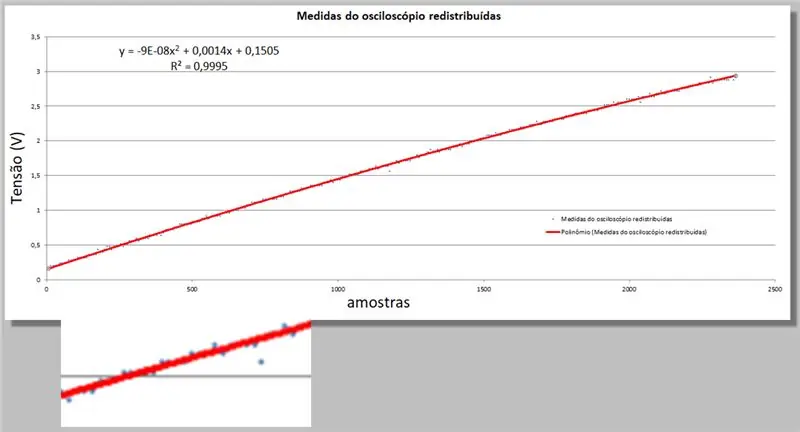
Το Excel μας δίνει δύο νέες πληροφορίες. η εξίσωση δεύτερης τάξης που ταιριάζει καλύτερα στα δεδομένα και η εξίσωση τετραγώνου R που ποσοτικοποιεί αυτήν την επάρκεια.

Απλώς θυμηθείτε ότι όσο πιο κοντά στο 1, τόσο πιο κατάλληλη είναι η εξίσωση.

Ας μην εμβαθύνουμε στα μαθηματικά, ας τα χρησιμοποιήσουμε απλά ως εργαλείο.

Βήμα 14: Συμπλήρωση των κενών - Αξιολόγηση της συνάρτησης

Ας συμπληρώσουμε τα κενά δειγματοληψίας με τα δεδομένα που δημιουργούνται από την εξίσωση. Και, στη συνέχεια, συγκρίνετέ τα με το σημείο.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Τάση παλμογράφου = -9E -08 * index2 + 0, 0014 * index + 0, 1505

Βήμα 15: Μετατροπή της τάσης του παλμογράφου σε ισοδύναμη τιμή για σύγκριση με το ADC

Ας το εκμεταλλευτούμε για να μετατρέψουμε επίσης την τιμή της τάσης του παλμογράφου σε ισοδύναμη τιμή ADC.

Καθώς η υψηλότερη τιμή που αποκτήθηκε στο ADP του ESP32 ήταν 4095, που ισοδυναμεί με την ένδειξη 2.958V για τον ίδιο δείκτη, μπορούμε να πούμε ότι:

Κάθε βολτ στις μετρήσεις του παλμογράφου ισούται περίπου με 1384,4 μονάδες του μ. Χ. Επομένως, μπορούμε να πολλαπλασιάσουμε όλες τις μετρήσεις του παλμογράφου με αυτήν την τιμή.

Βήμα 16: Σύγκριση των δύο ράμπων που λήφθηκαν

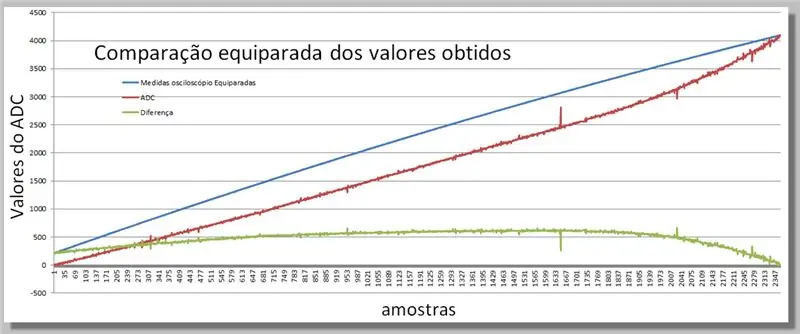
Οπτικοποίηση των διαφορών που προκύπτουν στις δύο αναγνώσεις.

Βήμα 17: Συμπεριφορά της διαφοράς ανάγνωσης ADC (ERROR)

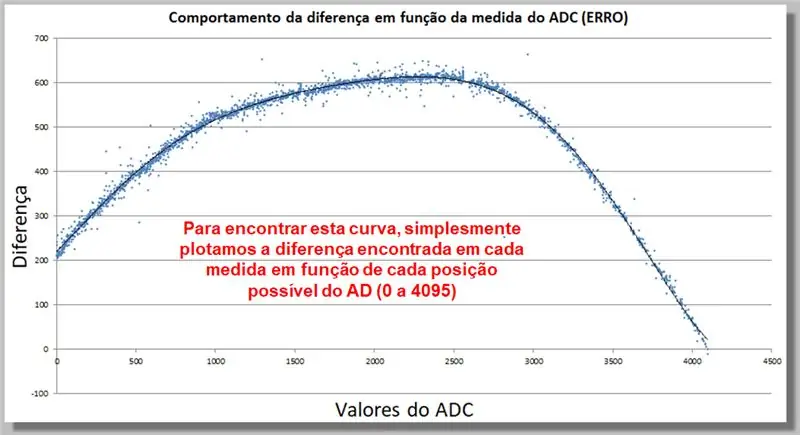
Η παρακάτω καμπύλη δείχνει πώς συμπεριφέρεται η διαφορά στην ανάγνωση ADC ως συνάρτηση της μέτρησης. Αυτή η συλλογή δεδομένων θα μας επιτρέψει να βρούμε μια λειτουργία διόρθωσης.

Για να βρούμε αυτήν την καμπύλη, απλώς σχεδιάζουμε τη διαφορά που βρίσκεται σε κάθε μέτρο ως συνάρτηση κάθε πιθανής θέσης AD (0 έως 4095).

Βήμα 18: Συμπεριφορά διαφοράς ανάγνωσης ADC - Εύρεση μιας συνάρτησης διόρθωσης

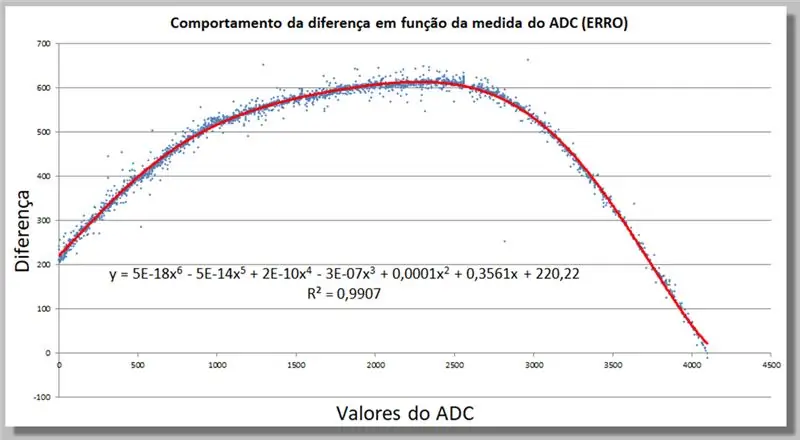
Μπορούμε να καθορίσουμε στο Excel μια λειτουργία διόρθωσης προσθέτοντας μια γραμμή τάσης, τώρα υψηλότερου βαθμού, μέχρι να ταιριάξει επαρκώς με τα δεδομένα μας.

Βήμα 19: Χρήση άλλου λογισμικού

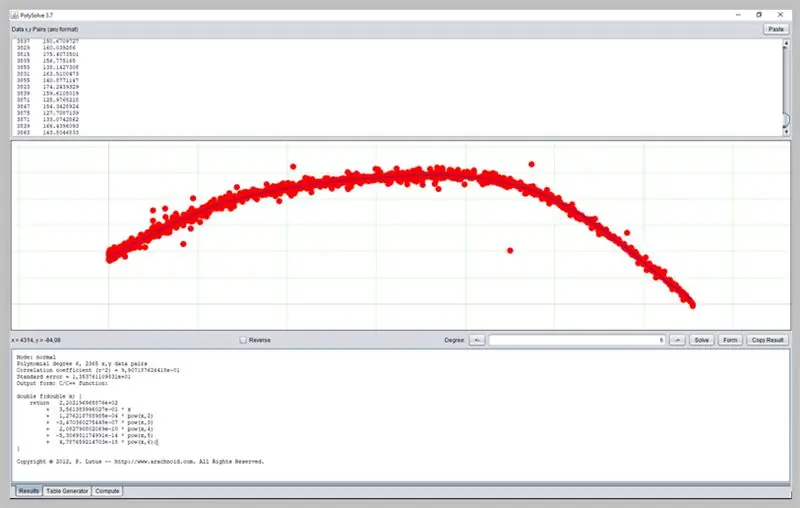
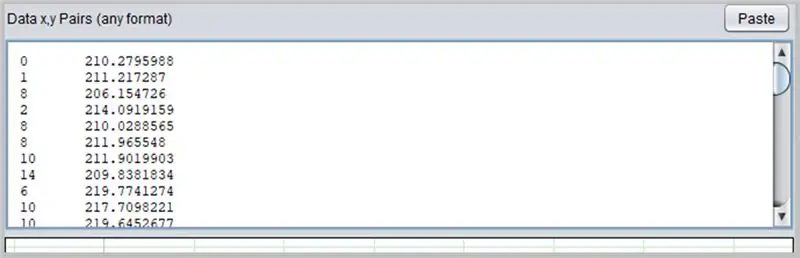
Ένα άλλο ενδιαφέρον λογισμικό για τον καθορισμό καμπυλών είναι το PolySolve, το οποίο μπορεί να χρησιμοποιηθεί απευθείας στον σύνδεσμο: https://arachnoid.com/polysolve/ ή να μεταφορτωθεί ως εφαρμογή Java.

Επιτρέπει την εφαρμογή πολυωνυμικών παλινδρόμησης υψηλότερου βαθμού και την παράδοση της μορφοποιημένης συνάρτησης, καθώς και άλλες λειτουργίες.

Για να το χρησιμοποιήσετε, απλά εισαγάγετε τα δεδομένα στο πρώτο πλαίσιο κειμένου. Τα δεδομένα πρέπει να ακολουθούν τη σειρά Χ, Υ που χωρίζονται με κόμμα ή καρτέλα. Να είστε προσεκτικοί όταν χρησιμοποιείτε σωστά την τελεία ως δεκαδικό σημείο.

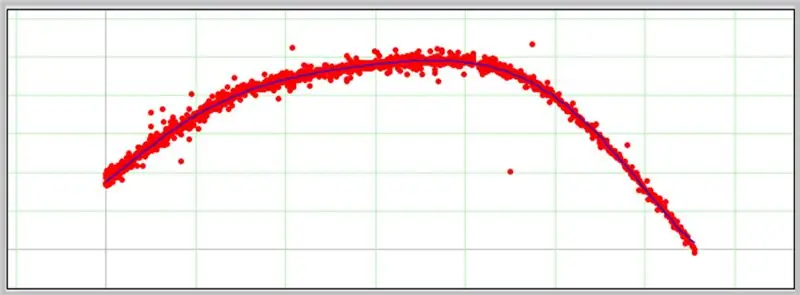
Ένα γράφημα θα εμφανιστεί στο επόμενο πλαίσιο εάν τα δεδομένα που έχουν εισαχθεί είναι σωστά μορφοποιημένα.

Δείτε πώς πήγε η καμπύλη σφάλματος ADC.

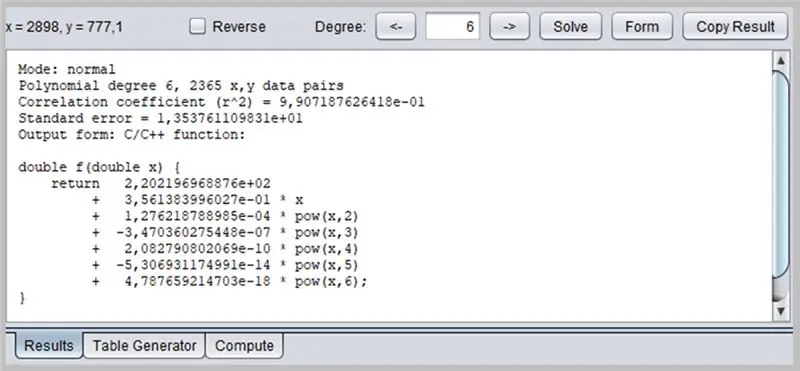
Αυτό το παράθυρο θα παρουσιάσει το αποτέλεσμα της παλινδρόμησης, συμπεριλαμβανομένων των δεδομένων επάρκειας συνάρτησης, τα οποία με τη σειρά τους μπορούν να μορφοποιήσουν την έξοδο με διάφορους τρόπους: ως συνάρτηση C / C ++, μια λίστα συντελεστών, μια συνάρτηση γραμμένη σε Java, κλπ.

Σημείωση: Δώστε προσοχή στους δεκαδικούς διαχωριστές

Βήμα 20: Σταθερές και ρύθμιση ()

Επισημαίνω εδώ το GPIO που χρησιμοποιήθηκε για αναλογική λήψη. Αρχικοποιώ τη σειριακή θύρα, καθώς και την ακίδα που έχει καθοριστεί για αναλογική λήψη.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Πραγματοποιήστε μια σειριακή είσοδο για το pinMode εντοπισμού σφαλμάτων (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Βήμα 21: Βρόχος () και η συνάρτηση διόρθωσης

Κάνουμε τη λήψη της προσαρμοσμένης τάσης και εκτυπώνουμε τις τιμές με ή χωρίς τις σωστές διορθώσεις.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Παρατηρήστε στη γραμμή 12 ότι έχουμε την επιλογή εκτύπωσης των δεδομένων με την προσθήκη της συνάρτησης διαφοράς f (analog_value).

Βήμα 22: Χρήση της λειτουργίας διόρθωσης PolySolve

Εδώ, χρησιμοποιούμε τη συνάρτηση PolySolve μέσα στο Arduino IDE.

/* Λειτουργία: κανονικός πολυωνυμικός βαθμός 6, 2365 x, y ζεύγη δεδομένων Συντελεστής συσχέτισης (r^2) = 9, 907187626418e-01 Τυπικό σφάλμα = 1, 353761109831e+01 Φόρμα εξόδου: Συνάρτηση C/C ++: Πνευματικά δικαιώματα © 2012, Σελ. Lutus - https://www.arachnoid.com. Ολα τα δικαιώματα διατηρούνται. */ διπλό f (διπλό x) {επιστροφή 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Σημειώστε την αλλαγή με κόμμα-τελεία ως δεκαδικός διαχωριστής.

Βήμα 23: Λήψη με διόρθωση - Σειριακό σχέδιο

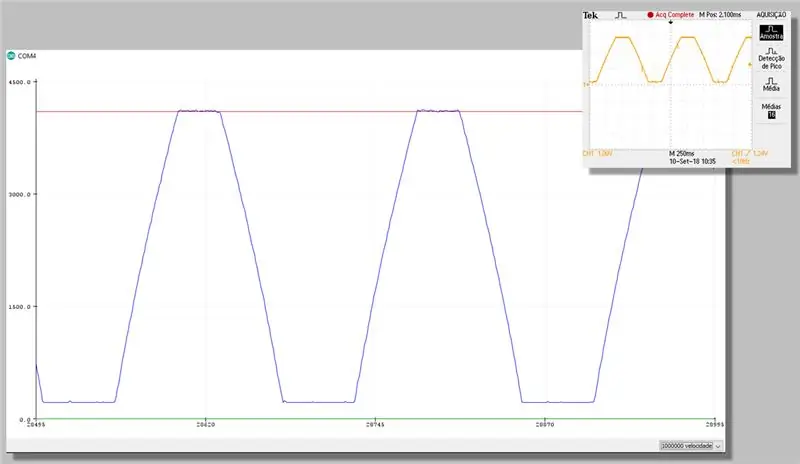
Βήμα 24: Υπολογιστικό κόστος

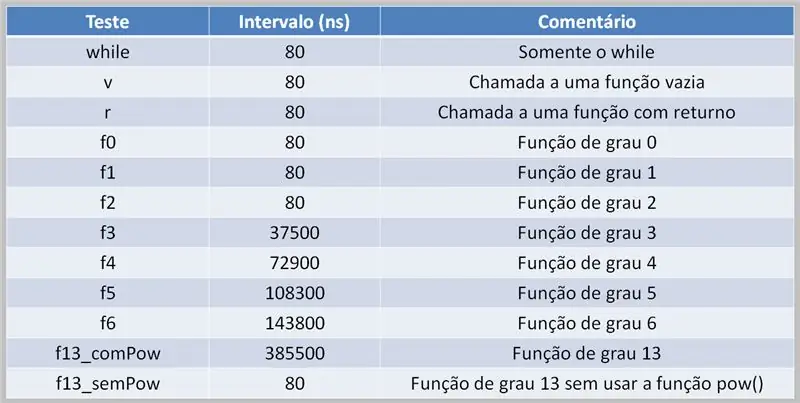
Για την εκτέλεση πολυωνυμικών υπολογισμών, είναι απαραίτητο ο επεξεργαστής να χειριστεί αυτήν την εργασία. Αυτό μπορεί να οδηγήσει σε καθυστερήσεις στην εκτέλεση, ανάλογα με τον πηγαίο κώδικα και τη διαθέσιμη υπολογιστική ισχύ.

Εδώ, βλέπουμε έναν πίνακα αποτελεσμάτων μιας δοκιμής που χρησιμοποιεί πολυώνυμα πολλαπλών βαθμών. Παρατηρήστε τη διαφορά μεταξύ των χρόνων που χρησιμοποιήθηκε η συνάρτηση pow () και όταν δεν ήταν.

Βήμα 25: Κωδικός δοκιμής - Ρύθμιση () και Εκκίνηση βρόχου ()

Εδώ, έχουμε τον κωδικό που χρησιμοποιήθηκε στη δοκιμή μας.

void setup () {Serial.begin (1000000); // Έναρξη σειριακού σήματος για debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0,0; // contador de chamadas

Βήμα 26: Κωδικός δοκιμής - Βρόχος () και Επεξεργασία

Χρησιμοποίησα τη λειτουργία micros () για να λάβω την τιμή σε δευτερόλεπτα.

// ============= inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // προσδιορισμός του διαστήματος που θα περάσει από την αρχή // ============== τελειώνει

Βήμα 27: Κωδικός δοκιμής - Βρόχος () - Αποτελέσματα

Εκτυπώνουμε την τιμή που επιστρέφεται από τη λειτουργία βαθμού 13 με και χωρίς POW για σύγκριση, καθώς και το διάστημα επεξεργασίας.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (αγορά, 6); }

Βήμα 28: Κωδικός δοκιμής - Χρησιμοποιημένες συναρτήσεις

Κενές λειτουργίες (μόνο με επιστροφή) βαθμού 0 και 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 διπλό f0 (διπλό x) {επιστροφή 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 διπλό f1 (διπλό x) {επιστροφή 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Λειτουργίες βαθμού 2, 3 και 4.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 διπλό f3 (διπλό x) {επιστροφή 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 διπλό f4 (διπλό x) {επιστροφή 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

Λειτουργίες βαθμού 5 και 6.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 διπλό f6 (διπλό x) {επιστροφή 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Λειτουργία βαθμού 13 χρησιμοποιώντας το POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Λειτουργία βαθμού 13 χωρίς χρήση POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Βήμα 29: Αρχεία

Κατεβάστε τα αρχεία:

PDF

ΕΓΩ ΔΕΝ

Υπολογιστικό φύλλο