Eyeballing Your Eyeball's Prescription: a BME60B Project: 9 Βήματα

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-30 08:32

Από: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Η μεγέθυνση είναι ένα από τα βασικά χαρακτηριστικά των γυαλιών ανάγνωσης, τα οποία ταξινομούνται με τη συνταγή διόπτρων. Σύμφωνα με το Τεχνολογικό Πανεπιστήμιο του Μίσιγκαν, η διόπτρα είναι το εστιακό μήκος του φακού, που συνήθως μετριέται σε mm, στη μονάδα μέτρων (Τεχνολογικό Πανεπιστήμιο του Μίσιγκαν). Επειδή τα γυαλιά ανάγνωσης έχουν κυρτούς φακούς, το εστιακό μήκος θα ήταν θετικό, προκαλώντας θετικές και τις διόπτρες (HyperPhysics). Το εστιακό μήκος αυξάνεται καθώς η απόσταση μεταξύ του αντικειμένου απομακρύνεται περισσότερο από τον πραγματικό φακό και αυτό οδηγεί τις διόπτρες να μειώνονται αφού είναι αντιστρόφως ανάλογες. Επομένως, η κατοχή γυαλιών ανάγνωσης με πρόσθετες διόπτρες θα βοηθούσε τον φακό να μεγεθύνει την προβολή, έτσι ώστε να φαίνεται ότι η εστιακή απόσταση είναι μικρότερη αυξάνοντας την τιμή των διοπτριών.

Ο κωδικός που παρουσιάζεται θα χρησιμοποιηθεί για την πρόβλεψη της διόπτρας ενός φακού με άγνωστη συνταγή. Δύο εισόδους χρησιμοποιούνται για τον υπολογισμό της συνταγής: μια φωτογραφία του ελεγχόμενου φόντου χωρίς τη χρήση φακών και μια άλλη φωτογραφία του ίδιου φόντου αλλά μέσω του φακού της επιλογής. Το πρόγραμμα θα μετρήσει την παραμόρφωση μεταξύ αυτών των δύο φωτογραφιών. Από εκεί, θα είμαστε σε θέση να εκτιμήσουμε τη διόπτρα του φακού και να παράγουμε ένα αποτέλεσμα για να το δει ο χρήστης.

Για αυτό το Instructable, θα χρειαστείτε:

• Ένα ασπρόμαυρο μοτίβο σκακιέρας τυπωμένο σε φύλλο χαρτιού 11x8,5
• Μια κάμερα με δυνατότητα κλειδώματος της εστίασης
• Τρίποδο ή κάτι παρόμοιο για να ασφαλίσετε την κάμερα
• Διάφορες συνταγές γυαλιών ανάγνωσης
• MATLAB

Βήμα 1: Λήψη φωτογραφιών

Για να υπολογίσετε τη μεγέθυνση ενός φακού, πρέπει να είστε σε θέση να τον συγκρίνετε με το πραγματικό μέγεθος του αντικειμένου. Για αυτό το έργο, θα συγκρίνουμε μια μεγεθυμένη εικόνα με μια εικόνα ελέγχου.

Έτσι, το πρώτο βήμα είναι να τραβήξετε δύο φωτογραφίες της ίδιας εικόνας - η πρώτη μέσω της κάμερας και η δεύτερη μέσω του φακού των γυαλιών ανάγνωσης που θέλετε να δοκιμάσετε.

Θα τραβήξετε μια φωτογραφία ενός ασπρόμαυρου πίνακα σκακιού 8,5x11in με ένα πλέγμα 1 ιντσών. Ρυθμίστε την κάμερά σας 11 μέτρα μακριά από τον πίνακα σκακιού. Πριν τραβήξετε τις φωτογραφίες, κλειδώστε την εστίαση στον πίνακα ελέγχου.

Τραβήξτε μια φωτογραφία της σκακιέρας χωρίς τα γυαλιά ανάγνωσης. Στη συνέχεια, χωρίς να μετακινήσετε τίποτα, τοποθετήστε τα γυαλιά ανάγνωσης μπροστά από την κάμερα και τραβήξτε τη δεύτερη φωτογραφία.

Βεβαιωθείτε ότι η θέση της κάμεράς σας δεν μετακινείται μεταξύ των λήψεων. Το μόνο που πρέπει να αλλάξει μεταξύ των δύο φωτογραφιών είναι η παρουσία του φακού γυαλιών μπροστά από την κάμερα.

Όταν τελειώσετε με τις φωτογραφίες, ανεβάστε τις στον υπολογιστή σας.

Βήμα 2: Φορτώστε τις εικόνες στο MATLAB

Ανοίξτε ένα νέο σενάριο.

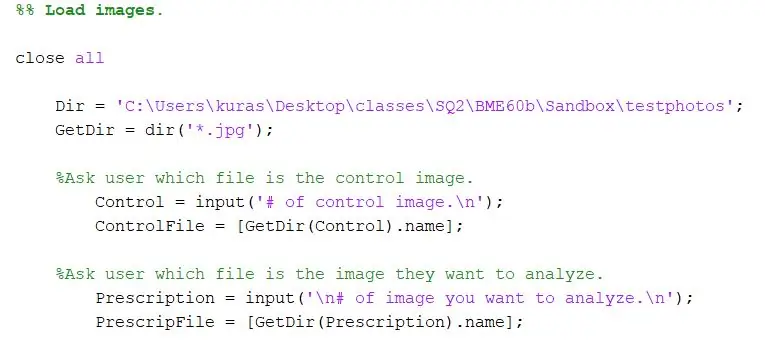
Αρχικά, καθορίστε τον κατάλογο όπου είναι αποθηκευμένες οι φωτογραφίες. Στη συνέχεια, χρησιμοποιήστε τη συνάρτηση dir για να εξαγάγετε εικόνες-j.webp

Dir = 'C: / Users / kuras / Desktop / class / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Για το έργο μας, θέλαμε να ζητήσουμε από τον χρήστη του προγράμματος για τα αρχεία που ήθελαν να συγκρίνουν. Η πρώτη ενότητα ζητά από τον χρήστη να καθορίσει την εικόνα ελέγχου και η δεύτερη ζητά από τον χρήστη να καθορίσει τη δοκιμαστική εικόνα.

• %Ρωτήστε τον χρήστη ποιο αρχείο είναι η εικόνα ελέγχου.
• Έλεγχος = είσοδος ('# εικόνας ελέγχου. / N');
• ControlFile = [GetDir (Control).name]
• %Ρωτήστε τον χρήστη ποιο αρχείο είναι η εικόνα που θέλει να αναλύσει.
• ChooseFile = είσοδος ('\ n# της εικόνας που θέλετε να αναλύσετε. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Βήμα 3: Ανάλυση εικόνας

Μια έγχρωμη εικόνα στο MATLAB είναι μεγέθους MxNx3, ενώ μια εικόνα κλίμακας του γκρι είναι MxN. Αυτό σημαίνει ότι είναι πιο γρήγορο να βελτιώσετε/επεξεργαστείτε μια εικόνα κλίμακας του γκρι, επειδή υπάρχουν λιγότερα δεδομένα για να παρακολουθείτε. Χρησιμοποιήστε το rgb2gray για να μετατρέψετε την εικόνα σε κλίμακα του γκρι. (Η λειτουργία imrotate χρησιμοποιήθηκε επειδή οι φωτογραφίες μας εμφανίστηκαν οριζόντια - αυτή η γραμμή κώδικα μπορεί να είναι ή να μην είναι απαραίτητη στην έκδοση σας.)

• %μετατροπή σε κλίμακα του γκρι και περιστροφή
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotate (I, 90);

Στη συνέχεια, εμφανίστε την εικόνα. Η συνάρτηση subplot χρησιμοποιείται έτσι ώστε η δοκιμαστική εικόνα να μπορεί να βρίσκεται δίπλα στο στοιχείο ελέγχου σε επόμενα βήματα.

• %απεικόνιση
• Φιγούρα 1);
• δευτερεύον οικόπεδο (1, 2, 1)
• imshow (I)?
• τίτλος (ControlFile);

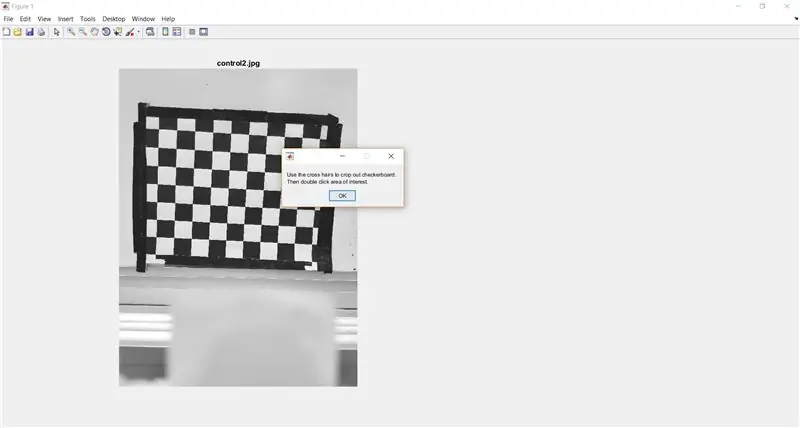
Χρησιμοποιήστε το imcrop για να ζητήσετε από τον χρήστη να περικόψει τον πίνακα ελέγχου από την πλήρη εικόνα. Ο παρακάτω κώδικας εμφανίζει επίσης ένα πλαίσιο μηνυμάτων για την παροχή οδηγιών στον χρήστη.

• %crop out checkerboard για ανάλυση
• waitfor (msgbox ({'Χρησιμοποιήστε τις σταυρωτές τρίχες για να περικόψετε τον πίνακα ελέγχου.', 'Στη συνέχεια κάντε διπλό κλικ στην περιοχή ενδιαφέροντος.'}));
• I_crop = imcrop (I);

Χρησιμοποιήστε το imbinarize για να δυαδικοποιήσετε την εικόνα.

I_binary = imbinarize (I_crop);

Βήμα 4: Υπολογίστε το πλάτος των λευκών τετραγώνων στον πίνακα ελέγχου

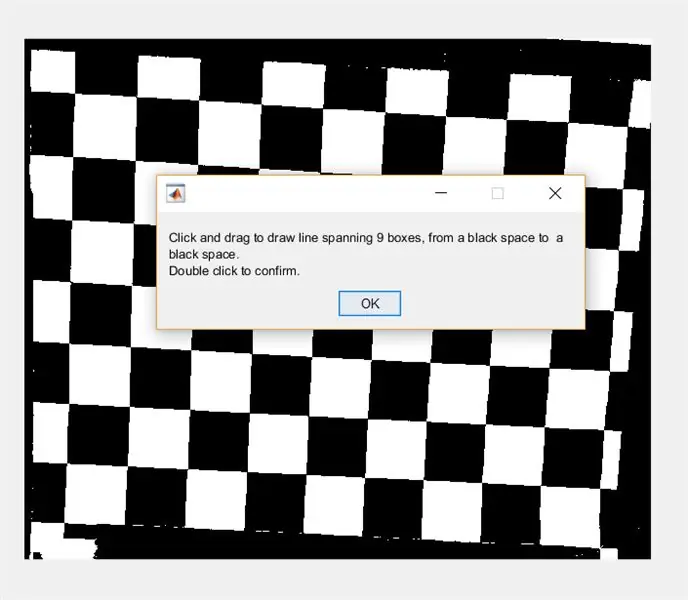
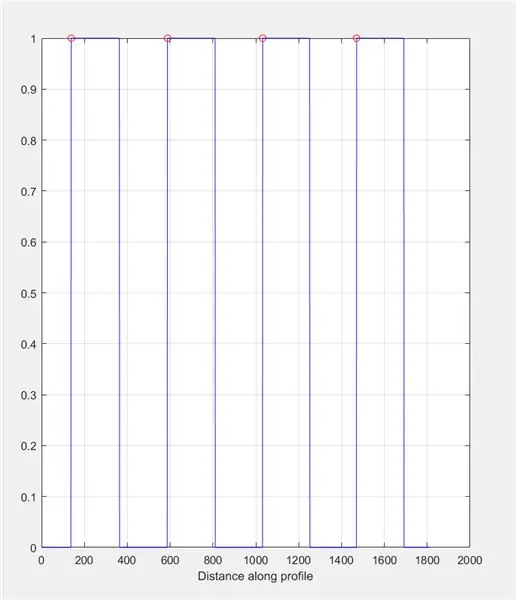
Στη συνέχεια, ζητήστε από τον χρήστη να σχεδιάσει μια γραμμή στην εικόνα χρησιμοποιώντας το imline. Αυτή η γραμμή πρέπει να εκτελείται οριζόντια κατά μήκος της σκακιέρας. Θα πρέπει να ξεκινά και να τελειώνει σε ένα μαύρο τετράγωνο (δεν έχει σημασία πού)- αυτό συμβαίνει επειδή θα μετρήσουμε το πλάτος των λευκών τετραγώνων, όχι των μαύρων.

• %σύρετε τη γραμμή
• Φιγούρα 1)
• δευτερεύον οικόπεδο (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Κάντε κλικ και σύρετε για να σχεδιάσετε τη γραμμή που εκτείνεται σε 9 πλαίσια, από ένα μαύρο διάστημα σε ένα μαύρο διάστημα.', 'Διπλό κλικ για επιβεβαίωση.'}));
• γραμμή = imline;
• θέση = αναμονή (γραμμή)?
• τελικά σημεία = line.getPosition;

Εξαγάγετε τα κουδουνικά X και Y για τα τελικά σημεία της γραμμής που τραβήξατε.

• X = τελικά σημεία (:, 1)
• Y = τελικά σημεία (:, 2);

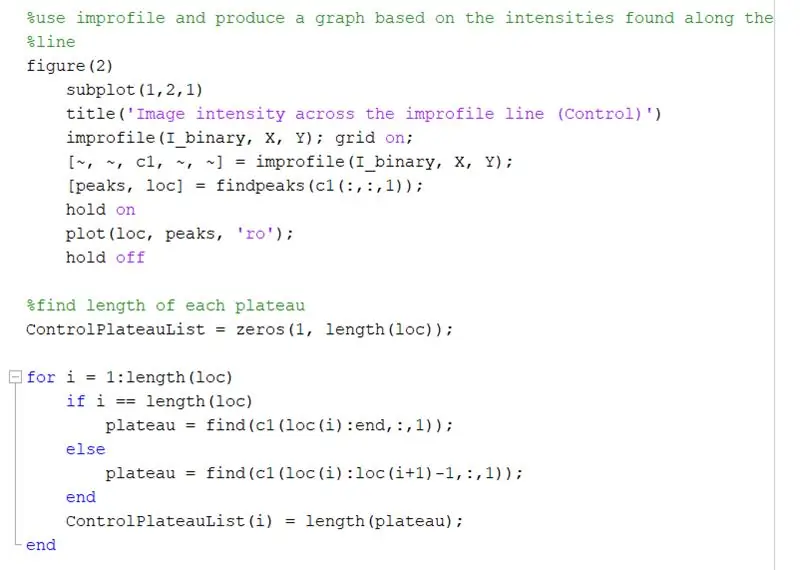
Χρησιμοποιήστε το improfile για να δημιουργήσετε μια γραφική παράσταση με βάση τις εντάσεις που βρίσκονται κατά μήκος της γραμμής. Αυτό πρέπει να μοιάζει με ένα τετράγωνο κύμα που κυμαίνεται από 0 (μαύρο) έως 1 (λευκό). Υπολογίστε επίσης τις κορυφές και τις θέσεις τους.

• Σχήμα 2)
• δευτερεύον οικόπεδο (1, 2, 1)
• τίτλος ("Ένταση εικόνας σε όλη τη γραμμή απενεργοποίησης (Έλεγχος)")
• improfile (I_binary, X, Y); πλέγμα ενεργοποιημένο?
• [~, ~, c1,, ~] = improfile (I_binary, X, Y);
• [κορυφές, loc] = findpeaks (c1 (:,:, 1));
• περίμενε
• οικόπεδο (loc, κορυφές, 'ro')?
• υπομονή

Βρείτε το μήκος κάθε οροπεδίου στο γράφημα improfile χρησιμοποιώντας έναν βρόχο for. Εκτελέστε τον βρόχο for για την ίδια ποσότητα κορυφών που υπάρχουν στο γράφημα απενεργοποίησης. Για να υπολογίσετε το μήκος κάθε οροπεδίου, χρησιμοποιήστε τη συνάρτηση «εύρεση» για να βρείτε όλες τις θέσεις όπου υπάρχει «1» αντί για τιμή έντασης «0». Στη συνέχεια, υπολογίστε το μήκος αυτού του πίνακα για να πάρετε το συνολικό μήκος του οροπεδίου, το οποίο θα πρέπει να ισούται με το πλάτος ενός λευκού τετραγώνου σε pixel. ControlPlateauList = μηδενικά (1, μήκος (loc));

για i = 1: μήκος (loc)

αν i == μήκος (loc)

οροπέδιο = εύρεση (c1 (loc (i): τέλος,:, 1));

αλλού

οροπέδιο = εύρεση (c1 (loc (i): loc (i+1) -1,:, 1));

τέλος

ControlPlateauList (i) = μήκος (οροπέδιο).

τέλος

Βήμα 5: Επαναλάβετε τα βήματα 3 και 4 για τη δοκιμαστική εικόνα

*Σημείωση: όταν σχεδιάζετε τη γραμμή απενεργοποίησης στη δοκιμαστική εικόνα, φροντίστε να την σχεδιάσετε στα τετράγωνα που αντιστοιχούν στη γραμμή που σχεδιάσατε στην εικόνα ελέγχου.

Βήμα 6: Υπολογίστε τη μεγέθυνση του φακού

Οι μεγεθυμένες μετρήσεις υπολογίζονται διαιρώντας τη μέση τιμή του μήκους του οροπεδίου, που υπολογίστηκε στο βήμα 5, με το μέσο μήκος του οροπεδίου ελέγχου, το οποίο υπολογίστηκε στο βήμα 4. Αυτό υπολογίζεται ότι είναι 1.0884.

μεγέθυνση = μέσος όρος (λίστα οροπεδίων)/μέσος όρος (ControlPlateauList);

Βήμα 7: Εύρεση τετραγώνου R και συνταγή χρήστη μέσω παρεμβολής

Χρησιμοποιώντας τον κωδικό:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Μπορούμε να βρούμε την τιμή του τετραγώνου R του γραφήματος GivenPresciption (οι τιμές των φακών μας) έναντι του MagArray (μια συστοιχία των λόγων μετρήσεων μεγέθυνσης που υπολογίσαμε νωρίτερα). Έχοντας μια αρκετά υψηλή τετραγωνική τιμή R, μπορούμε να συμπεράνουμε ότι υπάρχει ένας αρκετά ισχυρός συσχετισμός που δικαιολογεί τη χρήση αυτής της μεθόδου. Για τη συγκεκριμένη περίπτωση, η τιμή του τετραγώνου R ήταν 0,9912, γεγονός που υποδηλώνει ισχυρή συσχέτιση και ως εκ τούτου δικαιολογείται η χρήση αυτής της μεθόδου στην ανάλυση.

Χρησιμοποιώντας τη συνάρτηση:

Συνταγή = interp1 (MagArray, GivenPrescription, μεγέθυνση, 'γραμμική');

Μπορούμε να παρεμβάλουμε την αντίστοιχη τιμή συνταγής (στον άξονα x) του λόγου μεγέθυνσης (τιμή στον άξονα y) και να βρούμε ποια είναι η συνταγή του χρήστη.

Η παρεμβολή δεδομένων είναι σημαντική για να λειτουργήσει αυτή η μέθοδος καθώς μας επιτρέπει να κάνουμε υποθέσεις για πληροφορίες που δεν έχουμε, με βάση τις πληροφορίες που έχουμε. Ενώ μια γραμμή βέλτιστης προσαρμογής θα ήταν τεχνικά ισχυρότερη υποψήφια για αυτήν την υπόθεση, η δημιουργία ορίων για τη μείωση του αριθμού των εξόδων εξυπηρετεί το ίδιο αποτέλεσμα με τα ούτως ή άλλως ομοιογενείς τιμές γυαλιών συνταγής. Αυτό εξηγείται σε επόμενα βήματα.

Βήμα 8: Εμφάνιση της συνταγής του χρήστη σε ένα γράφημα

Χρησιμοποιώντας τον ακόλουθο κώδικα:

• εικόνα;
• πλοκή (GivenPrescription, MagArray, '-g')
• περίμενε
• πλοκή (Συνταγή, μεγέθυνση, 'bp')
• υπομονή
• πλέγμα
• θρύλος («Δεδομένα», «Ενδιάμεσα σημεία», «Τοποθεσία», «ΒΔ»)

Μπορούμε να σχεδιάσουμε μια γραφική παράσταση που δείχνει τους Λόγους Μεγέθυνσης έναντι της Δοθείσας Συνταγής με μια πράσινη γραμμή και τα ευρεθέντα δεδομένα της υπολογιζόμενης μεγέθυνσής μας έναντι της παρεμβολής μας με ένα μπλε αστέρι. Στη συνέχεια, ο θρύλος επισημαίνει τον τίτλο, τον άξονα x και τον άξονα y και τοποθετεί τον θρύλο στην επάνω αριστερή γωνία.

Βήμα 9: Περιορίστε τη συνταγή σας

Ο ακόλουθος κωδικός χρησιμοποιείται για την παραγωγή της στρογγυλοποίησης για τη συνταγή:

• εάν Συνταγή <= 1,125

  CalculatedPrescription = '1.0';

• elseif Συνταγή <= 1.375

  CalculatedPrescription = '1,25';

• elseif Συνταγή <= 1,625

  CalculatedPrescription = '1,5';

• elseif Συνταγή <= 1,875

  CalculatedPrescription = '1,75';

• elseif Συνταγή <= 2,25

  CalculatedPrescription = '2.0';

• elseif Συνταγή <= 2,625

  CalculatedPrescription = '2,5';

• elseif Συνταγή <= 3

  CalculatedPrescription = '2,75';

• elseif Συνταγή <= 3,375

  CalculatedPrescription = '3,25';

• αλλού

  CalculatedPrescription = 'άγνωστο';

• τέλος

Η συνταγή που βρέθηκε μέσω παρεμβολής δεν αντικατοπτρίζει απαραίτητα την πραγματική συνταγή - αυτό συμβαίνει γιατί πάντα θα υπάρχουν μικρές παραλλαγές στην ανάλυση της φωτογραφίας λόγω ανθρώπινου λάθους. Έτσι, χρειαζόμαστε αυτό το βήμα για να ταξινομήσουμε την πραγματική συνταγή.

Οι συνταγές που δίνονται συνήθως ξεκινούν από 1,0 διόπτρα και αυξάνονται κατά 0,25 στις συνταγές τους, οπότε μετά τον υπολογισμό της συνταγής θέλουμε να καθορίσουμε τη συνταγή που ταιριάζει καλύτερα σε αυτό που μπορεί να χρειαστεί ο χρήστης. Αφού υπολογίσουμε τη συνταγή, την εκτελούμε μέσω των δηλώσεων If για να ελέγξουμε την αξία της και να καθορίσουμε ποια συνταγή είναι απαραίτητη. Οτιδήποτε μικρότερο ή ίσο με 1,125, τότε η συνταγή είναι 1,0. Οτιδήποτε μικρότερο ή ίσο με 1,375, η συνταγή είναι 1,25. Οτιδήποτε μικρότερο ή ίσο με 1,625, η συνταγή είναι 1,5. Οτιδήποτε μικρότερο ή ίσο με 1,845, η συνταγή είναι 1,75. Και ούτω καθεξής.

Έχουμε τις τιμές να αυξάνονται αφού ελέγχουμε αν οι τιμές είναι μικρότερες από. Εάν μειώσουμε τις τιμές, τότε η πρώτη πρόταση if θα διαβάζει την πρώτη πρόταση συνεχώς. Εάν η συνταγή είναι η μικρότερη, θέλουμε να την αναγνωρίσει ως τη μικρότερη αμέσως, οπότε η μικρότερη αξία είναι αυτή που ξεκινήσαμε. Οτιδήποτε υψηλότερο από την υψηλότερη τιμή σημαίνει ότι η συνταγή δεν είναι σε εμβέλεια με τα δεδομένα μας, επομένως θα δώσει την ένδειξη "Άγνωστο" συμβολοσειρά.