
Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:32.
- Τελευταία τροποποίηση 2025-01-23 14:39.


Εδώ είναι μια πρακτική εφαρμογή σύνθετων μαθηματικών εξισώσεων.
Αυτή είναι στην πραγματικότητα μια πολύ χρήσιμη τεχνική που μπορείτε να χρησιμοποιήσετε για να χαρακτηρίσετε εξαρτήματα, ή ακόμα και μια κεραία, σε προκαθορισμένες συχνότητες.
Εάν ασχολείστε με τα ηλεκτρονικά, ίσως να είστε εξοικειωμένοι με το Resistors και το νόμο του Ohm. Δηλ. R = V / I mayσως εκπλαγείτε τώρα που γνωρίζετε ότι αυτό είναι το μόνο που πρέπει να λύσετε και για σύνθετη σύνθετη αντίσταση! Όλες οι αντίσταση είναι ουσιαστικά περίπλοκες, δηλαδή έχουν ένα πραγματικό και ένα φανταστικό μέρος. Στην περίπτωση ενός Resistor το φανταστικό (ή αντίσταση) είναι 0, αντίστοιχα δεν υπάρχει διαφορά φάσης μεταξύ V και I, οπότε μπορούμε να τα αφήσουμε εκτός.
Μια σύντομη περίληψη για μιγαδικούς αριθμούς. Σύνθετο σημαίνει απλώς ότι ο αριθμός αποτελείται από δύο μέρη, ένα πραγματικό και ένα φανταστικό. Υπάρχουν δύο τρόποι αναπαράστασης μιγαδικών αριθμών, για παράδειγμα στο παραπάνω σχήμα, ένα σημείο θα μπορούσε να οριστεί από τις πραγματικές και τις φανταστικές τιμές, όπως το σημείο όπου συναντώνται οι κίτρινες και μπλε γραμμές. Για παράδειγμα, αν η μπλε γραμμή ήταν στο 4 στον άξονα Χ και 3 στον άξονα Υ, αυτός ο αριθμός θα ήταν 4 + 3i, i δείχνει ότι αυτό είναι το φανταστικό μέρος αυτού του αριθμού. Ένας άλλος τρόπος για να ορίσετε το ίδιο σημείο θα ήταν το μήκος (ή το πλάτος) της κόκκινης γραμμής καθώς και η γωνία που έχει με την οριζόντια. Στο παραπάνω παράδειγμα αυτό θα ήταν 5 <36,87.
Or μια γραμμή με μήκος 5 σε γωνία 36,87 μοίρες.
Στην εξίσωση πάνω από όλες τις παραμέτρους, τα R, V και I μπορούν να θεωρηθούν ότι έχουν ένα φανταστικό μέρος, όταν δουλεύουμε με αντιστάσεις αυτή η τιμή είναι 0.
Όταν εργάζεστε με επαγωγείς ή πυκνωτές ή όταν μπορεί να μετρηθεί μια διαφορά φάσης (σε μοίρες) μεταξύ των σημάτων, η εξίσωση παραμένει η ίδια αλλά πρέπει να συμπεριληφθεί το φανταστικό μέρος του αριθμού. Οι περισσότεροι επιστημονικοί υπολογιστές καθιστούν την εργασία με πολύπλοκα μαθηματικά πολύ εύκολη, σε αυτό το σεμινάριο θα εργαστώ μέσω ενός παραδείγματος σε ένα Casio fx-9750GII.
Πρώτον, μια ανακεφαλαίωση στην εξίσωση του διαχωριστή τάσης αντίστασης.
Σύμφωνα με το σχήμα -
Η τάση στο Υ είναι ρεύμα i πολλαπλασιασμένη με R2
i είναι η τάση X διαιρούμενη με το άθροισμα των R1 και R2
Όταν το R2 είναι άγνωστο μπορούμε να μετρήσουμε τις άλλες τιμές, X, Y, R1 και να αναδιατάξουμε την εξίσωση για να λύσουμε για το R2.
Προμήθειες
Επιστημονικός υπολογιστής
Γεννήτρια σημάτων
Παλμοσκόπιο
Βήμα 1: Ρύθμιση

Ας υποθέσουμε ότι θέλουμε να υπολογίσουμε την επαγωγή της υπό δοκιμή συσκευής (DUT) στα 1MHz.
Η γεννήτρια σήματος έχει ρυθμιστεί για ημιτονοειδή έξοδο 5V σε 1MHZ.
Χρησιμοποιούμε αντιστάσεις 2k ohm και τα κανάλια παλμογράφων είναι CH1 και CH2
Βήμα 2: Παλιοσκόπιο

Παίρνουμε τις κυματομορφές όπως φαίνεται στο σχήμα. Μια μετατόπιση φάσης μπορεί να δει και να μετρηθεί στον παλμογράφο για να οδηγήσει κατά 130ns. Το πλάτος είναι 3,4V. Σημείωση, το σήμα στο CH1 πρέπει να είναι 2,5V όπως λαμβάνεται στην έξοδο του διαχωριστή τάσης, εδώ εμφανίζεται ως 5V για ευκρίνεια, καθώς αυτή είναι η τιμή που πρέπει επίσης να χρησιμοποιήσουμε στους υπολογισμούς μας. δηλ. 5V είναι η τάση εισόδου στον διαιρέτη με το άγνωστο στοιχείο.
Βήμα 3: Υπολογισμός φάσης

Στα 1MHz η περίοδος του σήματος εισόδου είναι 1us.
130ns δίνει αναλογία 0,13. Or 13%. Το 13% του 360 είναι 46,6
Στο σήμα 5V δίνεται γωνία 0.. καθώς αυτό είναι το σήμα εισόδου μας και η μετατόπιση φάσης είναι σχετική με αυτό.
στο σήμα 3,4V δίνεται η γωνία +46,6 (το + σημαίνει ότι οδηγεί, για έναν πυκνωτή η γωνία θα ήταν αρνητική).
Βήμα 4: Στην Αριθμομηχανή


Τώρα απλά εισάγουμε τις μετρημένες τιμές μας στην αριθμομηχανή.
Το R είναι 2k
Το V είναι 5 (ΕΠΕΞΕΡΓΑΣΙΑ - V είναι 5, αργότερα στην εξίσωση χρησιμοποιείται Χ! Το αποτέλεσμα είναι ακριβώς το ίδιο με το Χ που έχω το 5 στην αριθμομηχανή μου)
Y είναι η μετρημένη τάση μας με τη γωνία φάσης, ο αριθμός αυτός εισάγεται ως μιγαδικός αριθμός, απλώς καθορίζοντας τη γωνία όπως φαίνεται στην οθόνη της αριθμομηχανής
Βήμα 5: Λύστε την εξίσωση

τώρα η εξίσωση
(Υ * Ρ) / (Χ - Υ)
πληκτρολογείται στην αριθμομηχανή, αυτή είναι ακριβώς η ίδια εξίσωση που χρησιμοποιούμε για την επίλυση διαιρέσεων τάσης αντίστασης:)
Βήμα 6: Υπολογιζόμενες τιμές


Η αριθμομηχανή έδωσε το αποτέλεσμα
18 + 1872i
Το 18, είναι το πραγματικό μέρος της σύνθετης αντίστασης και έχει επαγωγή +1872 στο 1MHz.
Το οποίο λειτουργεί έως 298uH σύμφωνα με την εξίσωση σύνθετης αντίστασης επαγωγέα.
Τα 18 ohms είναι υψηλότερα από την αντίσταση που θα μετρήθηκε με ένα πολύμετρο, αυτό συμβαίνει επειδή το πολύμετρο μετρά την αντίσταση στο DC. Στα 1MHz υπάρχει φαινόμενο δέρματος, στο οποίο το εσωτερικό τμήμα του αγωγού παρακάμπτεται από το ρεύμα και ρέει μόνο στο εξωτερικό του χαλκού, μειώνοντας ουσιαστικά την εγκάρσια επιφάνεια του αγωγού και αυξάνοντας την αντίστασή του.
Συνιστάται:
Πώς να επιτύχετε οποιαδήποτε αντίσταση/χωρητικότητα χρησιμοποιώντας εξαρτήματα που έχετε ήδη !: 6 βήματα

Πώς να επιτύχετε οποιαδήποτε αντίσταση/χωρητικότητα χρησιμοποιώντας εξαρτήματα που έχετε ήδη!: Αυτός δεν είναι ένας ακόμη υπολογιστής σειράς/παράλληλης ισοδύναμης αντίστασης! Αυτό το πρόγραμμα υπολογίζει πώς να συνδυάσετε αντιστάσεις/πυκνωτές που έχετε αυτήν τη στιγμή για να επιτύχετε μια τιμή αντίστασης/χωρητικότητας που χρειάζεστε. Έχετε χρειαστεί ποτέ μια προδιαγραφή
MicroPython στον πίνακα αισθητήρων σύνθετων τεχνών: 3 βήματα

MicroPython στο Complex Arts Sensor Board: Μία από τις πιο εκπληκτικές πτυχές του μικροελεγκτή ESP32 είναι η ικανότητά του να εκτελεί MicroPython. Αυτό μπορεί να γίνει με δύο τρόπους: εκτέλεση πλήρων προγραμμάτων Python ή διαδραστικά μέσω εφαρμογής κονσόλας. Αυτό το Εγχειρίδιο θα δείξει πώς να χρησιμοποιείτε
Ξεθώριασμα/Έλεγχος Led/Φωτεινότητας Χρησιμοποιώντας Ποτενσιόμετρο (Μεταβλητή Αντίσταση) και Arduino Uno: 3 Βήματα
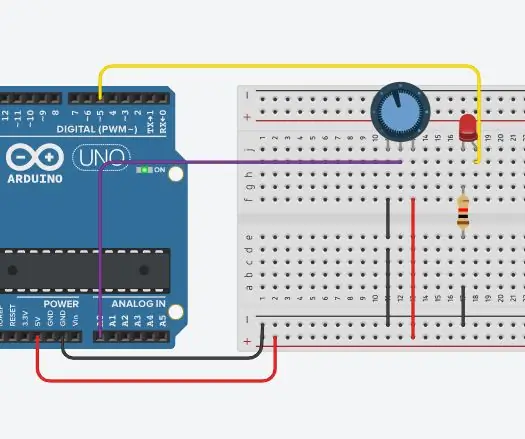
Ξεθώριασμα/Έλεγχος LED/φωτεινότητας Χρησιμοποιώντας Ποτενσιόμετρο (Μεταβλητή Αντίσταση) και Arduino Uno: Ο αναλογικός πείρος εισόδου Arduino συνδέεται στην έξοδο του ποτενσιόμετρου. Έτσι, ο αναλογικός πείρος Arduino ADC (αναλογικός σε ψηφιακός μετατροπέας) διαβάζει την τάση εξόδου από το ποτενσιόμετρο. Η περιστροφή του κουμπιού ποτενσιόμετρου μεταβάλλει την έξοδο τάσης και το Arduino επανα
Δημιουργία ήχων διαφορετικών ειδών με χρήση μαθηματικών εξισώσεων (MathsMusic) Arduino: 5 βήματα

Δημιουργία τόνων διαφορετικών ειδών με χρήση μαθηματικών εξισώσεων (MathsMusic) Arduino: Περιγραφή έργου: Ένα νέο ταξίδι έχει ξεκινήσει όπου οι ιδέες μπορούν να υλοποιηθούν εύκολα χρησιμοποιώντας κοινότητα ανοιχτού κώδικα (Χάρη στο Arduino). Ιδού λοιπόν ένας τρόπος · Κοιτάξτε γύρω σας και παρατηρήστε το περιβάλλον σας · Ανακαλύψτε προβλήματα που πρέπει να
Μεγάλη έκδοση του 1 Ohm Smd Resistor που παρέχει αντίσταση 1 Ohm χωρίς χρήση ηλεκτρονικών εξαρτημάτων .: 13 βήματα

Μεγάλη έκδοση του 1 Ohm Smd Resistor που παρέχει αντίσταση 1 Ohm χωρίς χρήση ηλεκτρονικών εξαρτημάτων .: Στην πραγματική ζωή οι αντιστάσεις smd είναι πολύ μικρές διαστάσεων σχεδόν 0,8mmx1,2mm. Εδώ, θα φτιάξω μια μεγάλη αντίσταση smd η οποία είναι πολύ τεράστια σε σύγκριση με την αντίσταση smd της πραγματικής ζωής
