Επίλυση πινάκων αλήθειας: 10 βήματα

2025 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2025-01-23 14:39

Ένας πίνακας αλήθειας είναι ένας τρόπος απεικόνισης όλων των αποτελεσμάτων ενός προβλήματος. Αυτό το σύνολο οδηγιών έχει σχεδιαστεί για άτομα που ξεκινούν τα διακριτά μαθηματικά. Θα εξασκηθούμε σήμερα με ένα παράδειγμα προβλήματος που είναι ειδικό για αυτές τις οδηγίες. Θα χρειαστείτε λίγο ξυστό και ένα μολύβι για να απεικονίσετε το τραπέζι. Αυτό το πρόβλημα θα χρειαστεί περίπου 5 λεπτά για να ολοκληρωθεί για άτομα με προηγούμενη γνώση του θέματος και περίπου 10 λεπτά για αρχάριους.

Για αυτό το σύνολο οδηγιών, θα εστιάσουμε στο πρόβλημα ~ p Λ q. Χρησιμοποιούμε αυτό για να εισαγάγουμε ορισμένα σύμβολα που απαιτούνται για την ερμηνεία των πινάκων αλήθειας.

Βήμα 1: Κατανόηση των πινάκων αλήθειας

Ένας πίνακας αλήθειας είναι ένας τρόπος απεικόνισης όλων των δυνατοτήτων ενός προβλήματος. Η γνώση των πινάκων αλήθειας είναι βασική ανάγκη για διακριτά μαθηματικά. Εδώ, θα βρούμε όλα τα αποτελέσματα για την απλή εξίσωση του ~ p Λ q.

Βήμα 2: Γνώση των συμβόλων

Το πρώτο βήμα στον πίνακα αλήθειας είναι η κατανόηση των σημείων. Το «~» στο συγκεκριμένο πρόβλημα σημαίνει άρνηση. Το "p" και το "q" είναι και οι δύο μεταβλητές. Το «Λ» ισοδυναμεί με «και». Αυτή η εξίσωση διαβάζεται ως "όχι p και q", δηλαδή, η εξίσωση είναι αληθινή εάν το p δεν είναι αληθές και το q είναι αληθινό.

Βήμα 3: Μορφοποίηση του πίνακα

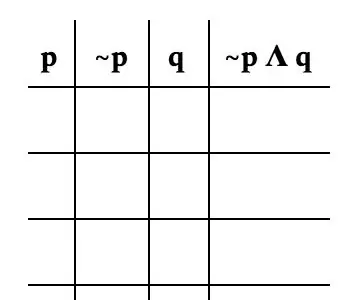
Τώρα για να σχηματίσετε τον πραγματικό πίνακα. Είναι σημαντικό να σπάσουμε το πρόβλημα ανά μεταβλητή. Για αυτό το πρόβλημα, θα το διασπάσουμε ως εξής: p, ~ p, q και ~ p Λ q. Η εικόνα είναι ένα καλό παράδειγμα για το πώς πρέπει να μοιάζει το τραπέζι σας.

Βήμα 4: Αντιστοίχιση Σωστό και Λάθος

Δεδομένου ότι υπάρχουν μόνο δύο μεταβλητές, θα υπάρχουν μόνο τέσσερις δυνατότητες ανά μεταβλητή. Για το p, το χωρίζουμε με τα μισά διαστήματα που παίρνει το T (για αληθινό) και το άλλο μισό με το F (για το ψευδές).

Βήμα 5: Άρνηση

Για ~ p, γράφετε το αντίθετο πρόσημο που έχει το p αφού το ~ p είναι το αντίθετο του p.

Βήμα 6: Μεταβλητή "q"

Για το q, εναλλάσσετε μεταξύ T και F για να πάρετε κάθε πιθανό συνδυασμό. Δεδομένου ότι η εξίσωση επικεντρώνεται μόνο στο ~ p, μπορούμε να αγνοήσουμε τη στήλη p όταν καθορίζουμε την αλήθεια της εξίσωσης. Το σύμβολο «Λ» σημαίνει ότι τόσο το ~ p όσο και το q πρέπει να είναι αληθινά για να είναι αληθινή η εξίσωση.

Βήμα 7: Επίλυση για το ψεύτικο στην τελευταία στήλη

Για την πρώτη σειρά, αφού ~ p είναι F και q είναι T, ~ p Λ q είναι F στο σενάριο ότι ~ p είναι F και q είναι Τ. Το μόνο σενάριο είναι ότι η εξίσωση είναι T όπου ~ p είναι T και q είναι Τ.

Βήμα 8: Εύρεση του αληθινού στην τελευταία στήλη

Αυτό σημαίνει ότι η μόνη σειρά που είναι Τ είναι η τρίτη.

Βήμα 9: Ολοκληρώνοντας τον πίνακα

Ελέγξτε ξανά ότι το τραπέζι σας είναι σωστό. Το κάνετε αυτό ελέγχοντας ότι τα σημάδια σας είναι σωστά και βεβαιωθείτε ότι η τελευταία στήλη έχει γίνει σωστά. Η τελευταία στήλη είναι το αποτέλεσμα όλων των πιθανών μεταθέσεων από τις μεταβλητές.

Βήμα 10: Έγινε

Τώρα που ξέρετε πώς να κάνετε έναν βασικό πίνακα αλήθειας, συνεχίστε να εξασκείστε! Όσο περισσότερο εξασκείστε, τόσο καλύτερα θα τα κάνετε.