
Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:37.
- Τελευταία τροποποίηση 2025-01-23 14:39.

Γειά σου! Για να ικανοποιήσω το ενδιαφέρον μου για προγραμματισμό και ελπίζω να βοηθήσω το δικό σας, θα ήθελα να σας δείξω ένα 3D Viewer που κωδικοποίησα σε javascript. Αν θέλετε να κατανοήσετε περαιτέρω τα παιχνίδια 3D ή ακόμη και να δημιουργήσετε το δικό σας παιχνίδι 3D, αυτό το πρωτότυπο πρόγραμμα προβολής 3D είναι ιδανικό για εσάς.
Βήμα 1: Η θεωρία

Για να κατανοήσετε τη θεωρία αυτού του τρισδιάστατου θεατή, μπορείτε απλά να εξετάσετε τον τρόπο με τον οποίο βλέπετε το περιβάλλον σας (βοηθά να έχετε μόνο μία σημαντική πηγή φωτός). Σημειώσε ότι:
- Τα αντικείμενα που βρίσκονται πιο μακριά από εσάς καταλαμβάνουν ένα μικρότερο τμήμα του οπτικού σας πεδίου.
- Τα αντικείμενα που βρίσκονται πιο μακριά από την πηγή φωτός φαίνονται πιο σκούρα σε χρώμα.
- Καθώς οι επιφάνειες γίνονται πιο παράλληλες (λιγότερο κάθετες) με την πηγή φωτός, εμφανίζονται πιο σκούρες στο χρώμα.
Αποφάσισα να εκπροσωπήσω ένα οπτικό πεδίο με μια δέσμη γραμμών που προέρχονται από ένα μόνο σημείο (ανάλογο με τον βολβό του ματιού). Όπως μια σφαίρα ακίδων, οι γραμμές πρέπει να είναι ομοιόμορφα μεταξύ τους για να διασφαλιστεί ότι κάθε τμήμα του οπτικού πεδίου αντιπροσωπεύεται εξίσου. Στην παραπάνω εικόνα, παρατηρήστε πώς οι γραμμές που προέρχονται από τη σφαίρα ακίδων απομακρύνονται περισσότερο καθώς απομακρύνονται πιο μακριά από το κέντρο της μπάλας. Αυτό βοηθά στην οπτικοποίηση της εφαρμογής της παρατήρησης 1 από το πρόγραμμα καθώς η πυκνότητα των γραμμών μειώνεται καθώς τα αντικείμενα απομακρύνονται πιο μακριά από το κεντρικό σημείο.
Οι γραμμές είναι η βασική μονάδα όρασης στο πρόγραμμα και αντιστοιχίζονται σε ένα pixel στην οθόνη. Όταν μια γραμμή τέμνει ένα αντικείμενο, το αντίστοιχο pixel της χρωματίζεται με βάση την απόσταση από την πηγή φωτός και τη γωνία της από την πηγή φωτός.
Βήμα 2: Θεωρία εφαρμογής

Για απλοποίηση του προγράμματος, η πηγή φωτός είναι η ίδια με το κεντρικό σημείο (βολβός του ματιού: σημείο από το οποίο φαίνεται ο χάρτης και από όπου πηγάζουν οι γραμμές). Ανάλογα με το να κρατάτε ένα φως ακριβώς δίπλα στο πρόσωπό σας, αυτό εξαλείφει τις σκιές και επιτρέπει τον υπολογισμό της φωτεινότητας κάθε εικονοστοιχείου πολύ πιο εύκολα.
Το πρόγραμμα χρησιμοποιεί επίσης σφαιρικές συντεταγμένες, με κεντρικό σημείο της όρασης στην αρχή. Αυτό επιτρέπει στις γραμμές να δημιουργούνται εύκολα (καθεμία με ένα μοναδικό θήτα: οριζόντια γωνία και phi: κάθετη γωνία) και παρέχει τη βάση υπολογισμών. Γραμμές με το ίδιο θήτα αντιστοιχίζονται σε εικονοστοιχεία στην ίδια σειρά. Το phis των αντίστοιχων γωνιών αυξάνεται σε κάθε σειρά εικονοστοιχείων.
Για απλοποίηση των μαθηματικών, ο τρισδιάστατος χάρτης αποτελείται από επίπεδα με κοινή μεταβλητή (κοινή x, y ή z), ενώ οι άλλες δύο μη κοινές μεταβλητές περιορίζονται σε ένα εύρος, ολοκληρώνοντας τον ορισμό κάθε επιπέδου.
Για να κοιτάξετε γύρω με το ποντίκι, οι εξισώσεις του προγράμματος συντελούν σε κάθετη και οριζόντια περιστροφή κατά τη μετατροπή μεταξύ σφαιρικών και συστημάτων συντεταγμένων xyz. Αυτό έχει ως αποτέλεσμα να προδιαμορφώνει μια περιστροφή στο σύνολο των γραμμών όρασης "σφαίρα ακίδας".
Βήμα 3: Μαθηματικά
Οι ακόλουθες εξισώσεις επιτρέπουν στο πρόγραμμα να καθορίσει ποιες γραμμές τέμνουν κάθε αντικείμενο και πληροφορίες για κάθε τομή. Πήρα αυτές τις εξισώσεις από τις βασικές σφαιρικές εξισώσεις συντεταγμένων και τις εξισώσεις περιστροφής 2D:
r = απόσταση, t = theta (οριζόντια γωνία), p = phi (κάθετη γωνία), A = περιστροφή γύρω από τον άξονα Y (κατακόρυφη περιστροφή), B = περιστροφή γύρω από τον άξονα Z (οριζόντια περιστροφή)
Kx = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*cos (B) -inin (p)*sin (t)*sin (B)
Ky = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*sin (B)+sin (p)*sin (t)*cos (B)
Kz = -sin (p)*cos (t)*sin (A)+cos (p)*cos (A)
x = r*Kx
y = r*Ky
z = r*Kz
r^2 = x^2+y^2+z^2
φωτισμός = Klight/r*(Kx ή Ky ή Kz)
p = arccos ((x*sin (A)*cos (B)+y*sin (A)*sin (B)+z*cos (A))/r)
t = arccos ((x*cos (B)+y*sin (B) -p*sin (A)*cos (p))/(r*cos (A)*sin (p)))
Βήμα 4: Πρόγραμμα

Ελπίζω ότι αυτό το πρωτότυπο πρόγραμμα προβολής 3D σας βοήθησε να κατανοήσετε τη λειτουργία της τρισδιάστατης εικονικής πραγματικότητας. Με περισσότερη τελειοποίηση και κωδικοποίηση, αυτός ο θεατής έχει σίγουρα τη δυνατότητα να χρησιμοποιηθεί στην ανάπτυξη παιχνιδιών 3D.
Συνιστάται:
ESP32 COVID19 STATUS VIEWER: 4 Βήματα

ESP32 COVID19 STATUS VIEWER: Αυτό το έργο μόλις λάβει την κατάσταση του COCID19 σε μορφή json και εμφανιστεί στο OLED
Film Negative Viewer and Converter: 8 βήματα (με εικόνες)

Film Negative Viewer and Converter: Βρήκα άμεση ανάγκη να μπορώ να βλέπω και να καταγράφω γρήγορα αρνητικά παλιάς ταινίας. Είχα αρκετές εκατοντάδες για να τακτοποιήσω … Αναγνωρίζω ότι υπάρχουν διάφορες εφαρμογές για το έξυπνο τηλέφωνό μου, αλλά δεν μπόρεσα να έχω ικανοποιητικά αποτελέσματα, οπότε αυτό είναι που έκανα
Arduino Baby Monitor με Java Viewer: 8 βήματα (με εικόνες)
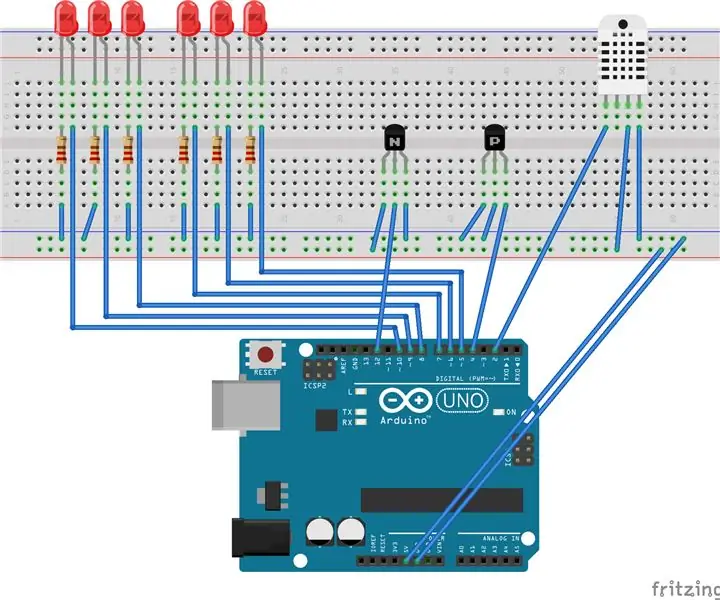
Arduino Baby Monitor With Java Viewer: Δημιουργήστε μια μονάδα πολλαπλών αισθητήρων με βάση το Arduino για να παρατηρείτε τις συνθήκες σε ένα δωμάτιο. Αυτή η μονάδα μπορεί να ανιχνεύσει υγρασία, θερμοκρασία, κίνηση και ήχο. Επισυνάπτεται ένα πρόγραμμα προβολής με βάση java που λαμβάνει σειριακά δεδομένα από το arduino
Headup Web Cam Viewer: 7 Βήματα

Headup Web Cam Viewer: Μια πρόσφατη καταχώρηση εξέτασε ένα εμπορικό σύστημα για να επιτρέψει στους χρήστες να κοιτάξουν απευθείας την κάμερα ιστού τους, ενώ εξακολουθούν να μπορούν να δουν το άτομο με το οποίο μιλούν - styleφος Teleprompter - Αυτή είναι η άποψή μου για αυτήν την ιδέα. Είναι εύκολο να κατασκευαστεί ως απαραίτητο
Photo Viewer Wrist Warmer: 5 Βήματα

Photo Viewer Wrist Warmer: Αγόρασα ένα από αυτά τα κλειδιά προβολής φωτογραφιών με κλειδί, ήταν μόνο ένα tenner, οπότε σκέφτηκα "ναι γιατί όχι, ίσως να είναι σε θέση να το χακάρει σε κάτι δροσερό". Έτσι, εμφανίζεται και το πρώτο πράγμα που κάνω με το? Τραβήξτε το και κολλήστε το σε θερμοστάτη καρπού
