
Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:37.
- Τελευταία τροποποίηση 2025-01-23 14:39.


Εάν έχετε οδηγήσει ποτέ ένα πλαίσιο τηλεχειριστηρίου, υπάρχει μια καλή πιθανότητα να έχετε χρησιμοποιήσει μίξη, ακόμα κι αν δεν το γνωρίζατε. Συγκεκριμένα, εάν έχετε χρησιμοποιήσει ένα μόνο joystick ή ένα gimble για τον έλεγχο ενός οχήματος που χρησιμοποιεί ολίσθηση ή διαφορικό τιμόνι, έχετε χρησιμοποιήσει μίξη.
Η μίξη είναι απλώς ο τρόπος με τον οποίο χρησιμοποιούνται τα δεδομένα από το joystick για να καθοριστεί πόση ισχύς πρέπει να παρέχεται σε κάθε πλευρά του πλαισίου.
Εάν ανοίξετε ένα χειριστήριο, γενικά θα δείτε δύο ποτενσιόμετρα μέσα. Το ένα για να μετρήσετε την τρέχουσα θέση σας κατά μήκος του άξονα Υ (πάνω και κάτω) και το άλλο για να μετρήσετε πού βρίσκεστε κατά μήκος του άξονα Χ (από πλευρά σε πλευρά).
Παρόλο που δεν έχω επίσημη εκπαίδευση στο θέμα, έπρεπε να κάνω μίξη σε κώδικα στο παρελθόν και πρόσφατα ήθελα να βουτήξω λίγο βαθύτερα στο θέμα.
Αρχικά θέλω να σημειώσω ότι οι περισσότεροι πομπούς RC έχουν δυνατότητα ανάμιξης όπως και πολλοί ελεγκτές κινητήρα. Αυτές οι πληροφορίες θα είναι πιο χρήσιμες εάν πρέπει να κάνετε τη μίξη μόνοι σας στον κώδικά σας. Πείτε για παράδειγμα εάν χρησιμοποιείτε Arduino για να διαβάζετε μη αναμεμειγμένα δεδομένα από δέκτη RC ή διαβάζετε αναλογικά δεδομένα από τα δοχεία σε ένα joystick ή αν διαβάζετε τις συντεταγμένες από ένα ψηφιακό joystick σε μια εφαρμογή για κινητά.
Ας ρίξουμε μια ματιά σε μερικές διαφορετικές προσεγγίσεις μίξης.
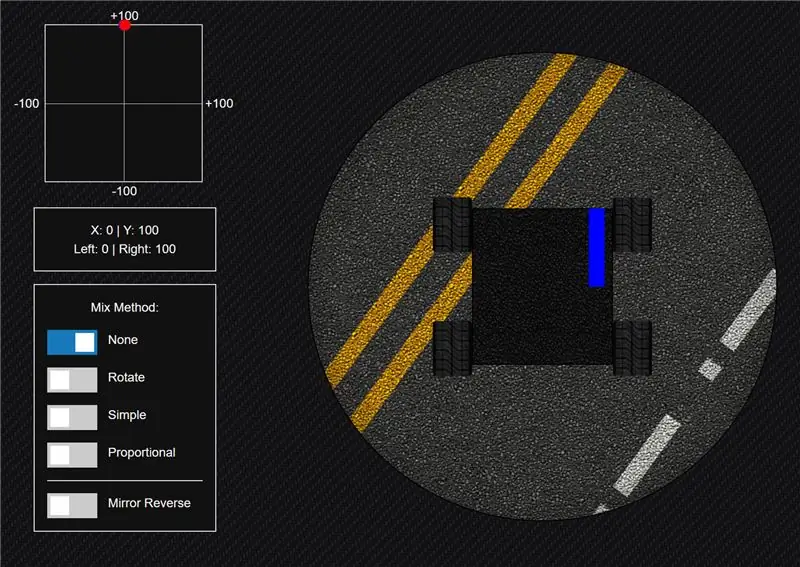
Βήμα 1: Μέθοδος ανάμειξης »Καμία
Αρχικά ας ρίξουμε μια ματιά στο τι συμβαίνει εάν δεν χρησιμοποιείτε καθόλου μίξη. Εάν απλώς στείλετε τα δεδομένα από τον έναν άξονα στη μία πλευρά του πλαισίου και τον άλλο άξονα στην άλλη πλευρά, το όχημά σας δεν θα ανταποκριθεί με τον τρόπο που θέλετε.
Για παράδειγμα, αν σπρώξετε το χειριστήριο εντελώς προς τα εμπρός, ο άξονας Υ βρίσκεται στο πλήρες γκάζι και ο άξονας Χ στο 0. Έτσι, θα οδηγούσατε σε κύκλους αντί να συνεχίσετε ευθεία.
Βήμα 2: Μέθοδος Μέθοδος »Περιστροφή
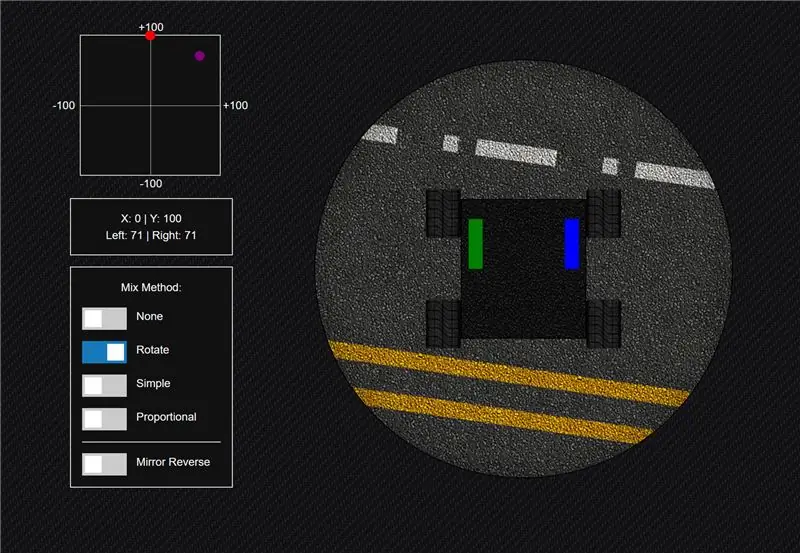
Ένας συνεργάτης μου είπε κάποτε ότι, με ένα τσίμπημα, μπορείτε να περιστρέψετε τον πομπό σας κατά 45 μοίρες για τη μίξη ενός φτωχού ανθρώπου. Αν σκεφτείτε ότι οι τιμές από τα δύο ποτενσιόμετρα σε ένα joystick είναι ο άξονας x an y σε ένα πλέγμα (και οι δύο άξονες εκτείνονται από -100 έως +100) αυτό έχει πολύ νόημα επειδή πρόκειται να +100 και στους δύο άξονες καθώς σπρώχνετε το χειριστήριο πάνω και δεξιά. Έτσι, εάν αυτό αντιστοιχεί απευθείας στα δύο κανάλια πλαισίου σας (στην αριστερή και δεξιά πλευρά του ρομπότ σας) θα έκανε το ρομπότ σας να προχωρήσει.
Έτσι, η πρώτη μέθοδος ανάμιξης που δοκίμασα ήταν να περιστρέψω μαθηματικά το συντεταγμένο x και y 45 μοίρες γύρω από το κεντρικό σημείο του πλέγματος.
Αυτό λειτουργεί εντάξει, ωστόσο δεν μπορώ να προχωρήσω με 100% ισχύ γιατί όταν περιστρέφεστε, η συνολική κίνηση περιορίζεται σε έναν κύκλο μέσα στο πλέγμα, πράγμα που σημαίνει ότι δεν μπορείτε ποτέ να μπείτε πραγματικά στην επάνω δεξιά γωνία.
Αυτό έχει επίσης ως αποτέλεσμα να μην χρησιμοποιούνται οι γωνίες του πλέγματος. Αυτό δεν είναι πρόβλημα εάν χρησιμοποιείτε ένα joystick/gimple που περιορίζει την κίνησή σας, έτσι ώστε να μην φτάσετε ποτέ σε αυτές τις περιοχές, αλλιώς θα θέλετε αυτό το τμήμα του πλέγματος να κάνει κάτι, έτσι ώστε οι κινήσεις σας να είναι εντελώς αναλογικές.
Εάν είστε οπτικός μαθητής όπως εγώ, αυτή η ιδέα μπορεί να είναι ευκολότερη να παρακολουθήσετε βλέποντας το βίντεο στην αρχή αυτού του διδακτικού.
Ας δούμε μερικά παραδείγματα κώδικα.
ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΤΟΥ ΚΩΔΙΚΟΥ ΜΟΥ: Αφήνω έξω πώς αποκτάτε τις τιμές του joystick_x και του joystick_y όπως θα άλλαζε ανάλογα με το έργο σας. Επίσης, θα χαρτογραφήσω/περιορίζω σε ± 100, αλλά πιθανόν να χρειαστεί να αντιστοιχίσετε σε 1000 - 2000 για PWM ή 0 - 255 για αναλογική έξοδο κλπ. Πάντα περιορίζω … για κάθε περίπτωση.
Παράδειγμα Arduino:
// περιστρέφεται μαθηματικά
διπλό rad = -45*M_PI/180; int leftThrottle = joystick_x * cos (rad) - joystick_y * sin (rad); int rightThrottle = joystick_y * cos (rad) + joystick_x * sin (rad); // περιορισμός leftThrottle = περιορισμός (leftThrottle, -100, 100); rightThrottle = περιορισμός (rightThrottle, -100, 100);
Παράδειγμα JavaScript:
// μαθηματικά rotatevar rad = -45*Math. PI/180; leftThrottle = joystick_x * Math.cos (rad) - joystick_y * Math.sin (rad); rightThrottle = joystick_y * Math.cos (rad) + joystick_x * Math.sin (rad); // constrainleftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = περιορισμός (rightThrottle, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };
Βήμα 3: Μέθοδος Μέθοδος »Απλό
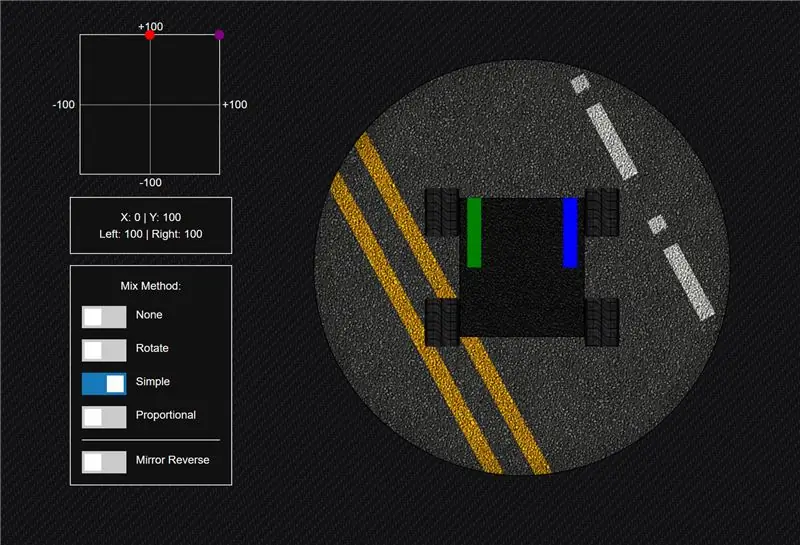
Στη συνέχεια έχουμε μια πολύ απλή εξίσωση την οποία πήρα για πρώτη φορά από ένα από τα βίντεο του Shawn Hymel's Adventures in Science SparkFun όπου έτυχε να δουλεύει ένα πολύ παρόμοιο έργο με αυτό που δούλευα.
Αυτή η εξίσωση σας επιτρέπει να φτάσετε σε πλήρη ταχύτητα όταν προχωράτε μπροστά, αλλά παρόμοια με τη μέθοδο περιστροφής, αγνοεί τις γωνιακές περιοχές του πλέγματος. Αυτό συμβαίνει επειδή σε ορισμένες περιπτώσεις το μέγιστο είναι 100 και σε ορισμένες περιπτώσεις το μέγιστο είναι 200. Έτσι, θα χρησιμοποιούσατε μια συνάρτηση περιορισμού για να αγνοήσετε οτιδήποτε μετά το 100.
Και παρεμπιπτόντως δεν το αποκαλώ υποτιμητικά … υπάρχει μια ομορφιά στην απλότητα.
Παράδειγμα Arduino:
int leftThrottle = joystick_y + joystick_x;
int rightThrottle = joystick_y - joystick_x; // περιορισμός leftThrottle = περιορισμός (leftThrottle, -100, 100); rightThrottle = περιορισμός (rightThrottle, -100, 100);
Παράδειγμα JavaScript:
var leftChannel = joystick_y + joystick_x;
var rightChannel = joystick_y - joystick_x; // περιορισμός leftChannel = περιορισμός (leftChannel, -100, 100); rightChannel = περιορισμός (rightChannel, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };
Βήμα 4: Μέθοδος Μέθοδος »Αναλογική
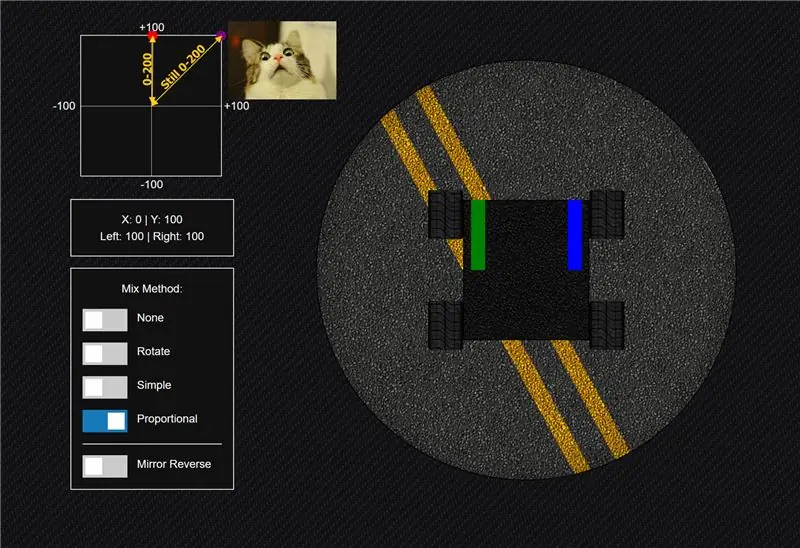
Ξεκίνησα από την απλή μέθοδο ελπίζοντας να κάνω το καλύτερο και από τις δύο εξισώσεις. Η ιδέα εδώ είναι να είναι πλήρως ανάλογη προς όλες τις κατευθύνσεις ακόμη και διαγώνια παρά το γεγονός ότι αν κινείστε σε μεγαλύτερη απόσταση έχει το ίδιο εύρος όπως όταν κινείτε κάθετα που είναι μικρότερη απόσταση.
Καταλήγετε με μια κλίμακα -200 έως +200 προς όλες τις κατευθύνσεις στα παραδείγματά μου, το αντιστοιχίζω σε 100 because επειδή αντιπροσωπεύει το ποσοστό ισχύος που πηγαίνει σε κάθε κανάλι - ωστόσο θα θέλετε να το αντιστοιχίσετε σε ό, τι λειτουργεί στη χρήση σας - θήκη για τον ελεγκτή κινητήρα σας. Για παράδειγμα, εάν στέλνετε ένα σήμα PWM, μπορείτε να το αντιστοιχίσετε σε 1000 έως 2000 ή εάν στέλνετε ένα αναλογικό σήμα, μπορείτε να το αντιστοιχίσετε σε 0-255 και να ορίσετε την κατεύθυνση ως boolean κ.λπ.
Παράδειγμα Arduino:
int leftThrottle = joystick_y + joystick_x;
int rightThrottle = joystick_y - joystick_x; // σε ορισμένες περιπτώσεις το μέγιστο είναι 100, σε ορισμένες περιπτώσεις είναι 200 // ας συνυπολογίσουμε τη διαφορά, οπότε το μέγιστο είναι πάντα 200int diff = abs (abs (joystick_y) - abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle - διαφορο: rightThrottle + διαφο? // Χάρτης από ± 200 έως ± 100 ή όποιο εύρος χρειάζεστε // constrainleftThrottle = περιορισμός (leftThrottle, -100, 100); rightThrottle = περιορισμός (rightThrottle, -100, 100);
Παράδειγμα JavaScript:
var leftThrottle = joystick_y + joystick_x; var rightThrottle = joystick_y - joystick_x; // σε ορισμένες περιπτώσεις το μέγιστο είναι 100, σε ορισμένες περιπτώσεις είναι 200, // ας συνυπολογίσουμε τη διαφορά, ώστε το μέγιστο να είναι πάντα 200var diff = Math.abs (Math.abs (joystick_y) - Math.abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle -diff: rightThrottle + diff; // Χάρτης από ± 200 πίσω έως 100 ± ή οτιδήποτε χρειάζεστεTeftottle = χάρτης (leftThrottle, -200, 200, -100, 100). -100, 100); // constrain leftThrottle = constrain (leftThrottle, -100, 100); rightThrottle = constrain (rightThrottle, -100, 100); // ορισμένες βοηθητικές λειτουργίεςvar constrain = λειτουργία (num, min, max) {return Math.min (Math max (num, min), max); }; var map = λειτουργία (num, inMin, inMax, outMin, outMax) {var p, inSpan, outSpan, mapped; inMin = inMin + inMax; num = num + inMax; inMax = inMax + inMax; inSpan = Math.abs (inMax-inMin); p = (num/inSpan)*100; outMin = outMin + outMax; outMax = outMax + outMax; outSpan = Math.abs (outMax - outMin); αντιστοιχισμένο = outSpan*(p/100) - (outMax/2); επιστροφή χαρτογραφήθηκε;};
Συνιστάται:
Ασύρματο τηλεχειριστήριο χρησιμοποιώντας μονάδα NRF24L01 2.4Ghz με Arduino - Nrf24l01 Δέκτης πομπού 4 καναλιών / 6 καναλιών για Quadcopter - Rc Ελικόπτερο - Rc Plane Using Arduino:
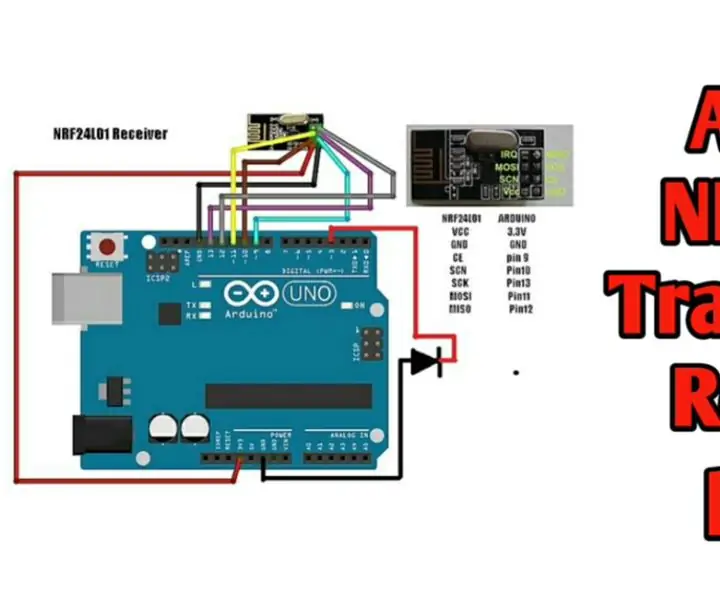
Ασύρματο τηλεχειριστήριο χρησιμοποιώντας μονάδα NRF24L01 2.4Ghz με Arduino | Nrf24l01 Δέκτης πομπού 4 καναλιών / 6 καναλιών για Quadcopter | Rc Ελικόπτερο | Rc Plane Using Arduino: Για να χειριστείτε ένα αυτοκίνητο Rc | Quadcopter | Drone | Αεροπλάνο RC | Σκάφος RC, χρειαζόμαστε πάντα έναν δέκτη και πομπό, ας υποθέσουμε ότι για το RC QUADCOPTER χρειαζόμαστε έναν πομπό και δέκτη 6 καναλιών και αυτός ο τύπος TX και RX είναι πολύ δαπανηρός, οπότε θα κάνουμε έναν
Κατανόηση του πρωτοκόλλου IR των τηλεχειριστηρίων του κλιματιστικού: 9 βήματα (με εικόνες)

Κατανόηση του πρωτοκόλλου IR των τηλεχειριστηρίων του Air Conditoner: Μαθαίνω για πρωτόκολλα IR εδώ και αρκετό καιρό τώρα. Πώς να στείλετε και να λάβετε σήματα IR. Σε αυτό το σημείο, το μόνο που απομένει είναι το πρωτόκολλο IR των τηλεχειριστηρίων AC. Σε αντίθεση με τα παραδοσιακά τηλεχειριστήρια σχεδόν όλων των ηλεκτρονικών συσκευών (ας πούμε μια τηλεόραση) όπου
Μπαταρία πατάτας: Κατανόηση της χημικής και ηλεκτρικής ενέργειας: 13 βήματα (με εικόνες)

Μπαταρία πατάτας: Κατανόηση της χημικής και ηλεκτρικής ενέργειας: Γνωρίζατε ότι μπορείτε να τροφοδοτήσετε έναν λαμπτήρα μόνο με μια πατάτα ή δύο; Η χημική ενέργεια μεταξύ των δύο μετάλλων μετατρέπεται σε ηλεκτρική και δημιουργεί ένα κύκλωμα με τη βοήθεια της πατάτας! Αυτό δημιουργεί ένα μικρό ηλεκτρικό φορτίο που μπορεί να
Δημιουργήστε έναν υπολογιστή με βασική κατανόηση των ηλεκτρονικών: 9 βήματα (με εικόνες)

Δημιουργήστε έναν υπολογιστή W/ Basic Understanding of Electronics: Θέλατε ποτέ να προσποιηθείτε ότι είστε πραγματικά έξυπνοι και να φτιάξετε τον υπολογιστή σας από την αρχή; Δεν γνωρίζετε τίποτα για το τι χρειάζεται για να φτιάξετε έναν ελάχιστο υπολογιστή; Λοιπόν, είναι εύκολο αν γνωρίζετε αρκετά για τα ηλεκτρονικά για να συνδυάσετε μερικά IC
Κατανόηση του ICSP για μικροελεγκτές PIC: 4 βήματα (με εικόνες)
Κατανόηση του ICSP για μικροελεγκτές PIC: Ο προγραμματισμός μικροελεγκτών δεν είναι δύσκολος. Η οικοδόμηση ενός προγραμματιστή κάνει ένα μεγάλο πρώτο ηλεκτρονικό έργο. Ο στόχος αυτού του διδάσκοντος είναι να εξηγήσει την απλή μέθοδο «σε σειριακό προγραμματισμό κυκλωμάτων» που χρησιμοποιείται με PIC μικροτσίπ
