Μέτρηση θερμοκρασίας από PT100 χρησιμοποιώντας Arduino: 6 βήματα (με εικόνες)

2024 Συγγραφέας: John Day | [email protected]. Τελευταία τροποποίηση: 2024-01-31 10:18

Ο PT100 είναι ένας ανιχνευτής θερμοκρασίας αντίστασης (RTD) ο οποίος αλλάζει την αντίστασή του ανάλογα με τη θερμοκρασία του περιβάλλοντός του, χρησιμοποιείται ευρέως για βιομηχανικές διαδικασίες με αργή δυναμική και σχετικά ευρεία κλίμακα θερμοκρασίας. Χρησιμοποιείται για αργές δυναμικές διεργασίες επειδή τα RTD έχουν αργούς χρόνους απόκρισης (για τους οποίους θα μιλήσω περισσότερο αργότερα) αλλά είναι ακριβείς και έχουν χαμηλή μετατόπιση με την πάροδο του χρόνου. Αυτό που θα σας δείξω σε αυτό το Instructable δεν είναι σύμφωνο με τα βιομηχανικά πρότυπα, αλλά θα σας εκθέσει σε έναν εναλλακτικό τρόπο μέτρησης της θερμοκρασίας από τη χρήση του LM35 που θα γνώριζαν πολλοί χομπίστες και η θεωρία κυκλώματος φαίνεται μπορεί να εφαρμοστεί σε άλλους αισθητήρες.

Βήμα 1: Στοιχεία

1x PT100 (δύο καλωδίων)

1x Arduino (οποιοδήποτε μοντέλο)

3x 741 ενισχυτές λειτουργίας (LM741 ή UA741)

Αντίσταση 1x 80ohm

2x 3.9kohms Αντιστάσεις

2x 3.3kohms Αντιστάσεις

2x 8,2kohms Αντιστάσεις

2x 47kohms Αντιστάσεις

Ποτενσιόμετρο 1x 5kohms

1x Δύο τερματικό τροφοδοτικό ή μπαταρίες AA 8x 1.5V

Χρησιμοποιώ ένα PT100 με δύο σύρματα, τα PT100 με τρία και τέσσερα σύρματα θα έχουν διαφορετικά κυκλώματα. Οι τιμές των αντιστάσεων για τα περισσότερα από αυτά δεν χρειάζεται να είναι ακριβώς ίδιες με τις παραπάνω, αλλά αν υπάρχει ένα ζευγάρι αντιστάσεων, δηλαδή το 3,9Kohms, αν τις αντικαταστήσατε για ας πούμε 5k, θα πρέπει να τις αλλάξετε και για 5k όπως και τότε πρέπει να είναι το ίδιο. Όταν πάρουμε το κύκλωμα θα πω το αποτέλεσμα της επιλογής διαφορετικών τιμών. Για τους ενισχυτές λειτουργίας (ενισχυτές op) μπορείτε να χρησιμοποιήσετε άλλους ενισχυτές op, αλλά αυτοί είναι που χρησιμοποίησα.

Βήμα 2: Γέφυρα Wheatstone

Πρώτα πρέπει να μιλήσω για τον τύπο για τη λήψη της θερμοκρασίας από την αντίσταση για το PT100 πριν μιλήσω για το πρώτο μέρος του κυκλώματος, ο τύπος για την αντίσταση είναι ο εξής:

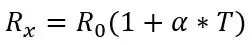
όπου Rx είναι η αντίσταση PT100, R0 είναι η αντίσταση PT100 στους 0 βαθμούς C, α είναι ο συντελεστής αντίστασης θερμοκρασίας και T είναι η θερμοκρασία.

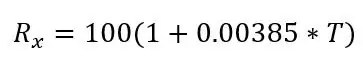
Το R0 είναι 100ohms καθώς αυτό είναι ένα PT100, αν ήταν PT1000, το R0 θα ήταν 1000ohms. Το α είναι 0,00385 ohms/βαθμοί C που λαμβάνονται από το φύλλο δεδομένων. Υπάρχει επίσης ένας πιο ακριβής τύπος που μπορεί να βρεθεί εδώ, αλλά ο παραπάνω τύπος θα κάνει για αυτό το έργο. Εάν μεταφέρουμε τον τύπο, μπορούμε να υπολογίσουμε τη θερμοκρασία για μια δεδομένη αντίσταση:

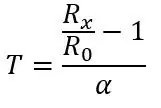
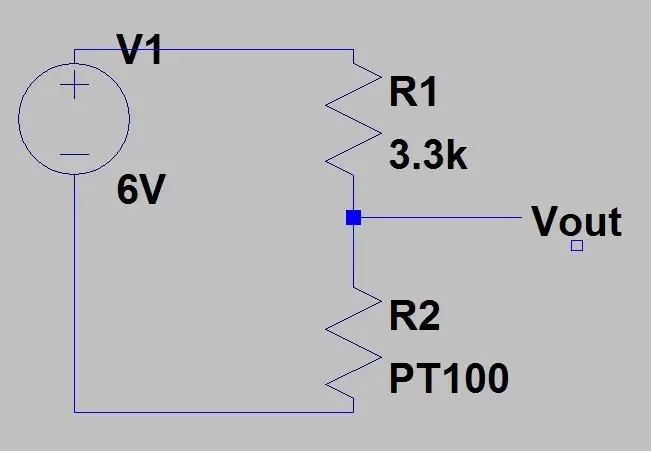
Ας υποθέσουμε ότι θέλουμε να μετρήσουμε κάτι που θα έχει εύρος θερμοκρασίας -51,85 έως 130 βαθμούς C και τοποθετήσαμε το PT100 στο κύκλωμα που φαίνεται στην εικόνα 1. Χρησιμοποιώντας την παραπάνω εξίσωση και την εξίσωση για την τάση εκτός ενός διαχωριστή τάσης (φαίνεται στην πρώτη εικόνα) μπορούμε να υπολογίσουμε το εύρος τάσης. Κάτω της περιοχής T = -51,85 (80ohms)

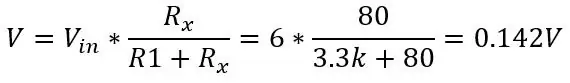
και στους 130 μοίρες (150ohms):

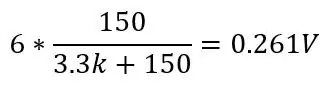
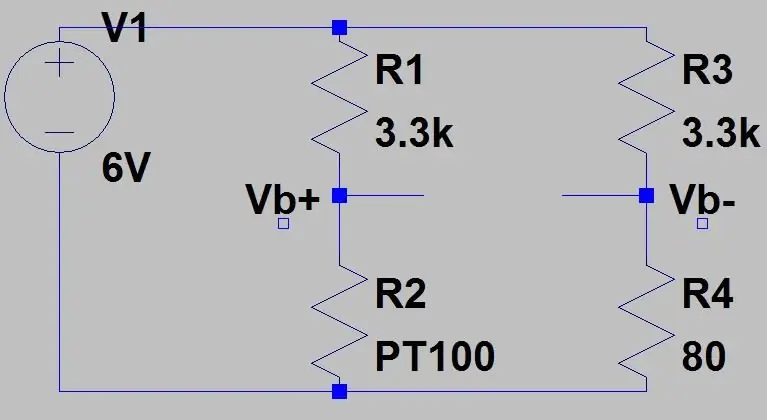
Αυτό θα έδινε μια περιοχή 0,1187V και μια μετατόπιση DC 0,142 επειδή γνωρίζουμε ότι η θερμοκρασία μας δεν θα πέσει ποτέ κάτω από τους -51,85 βαθμούς C, αυτό θα μειώσει την ευαισθησία στο εύρος που μας ενδιαφέρει (80 έως 130ohms) όταν ενισχύουμε αυτήν την τάση. Για να απαλλαγούμε από αυτή τη μετατόπιση DC και να αυξήσουμε την ευαισθησία μας, μπορούμε να χρησιμοποιήσουμε μια γέφυρα Wheatstone που φαίνεται στη δεύτερη εικόνα.

Η έξοδος του δεύτερου διαιρέτη τάσης (Vb-) θα αφαιρεθεί από την πρώτη έξοδο διαχωριστή τάσης (Vb+) χρησιμοποιώντας έναν διαφορικό ενισχυτή αργότερα. Ο τύπος για την έξοδο της γέφυρας είναι μόνο δύο διαχωριστές τάσης:

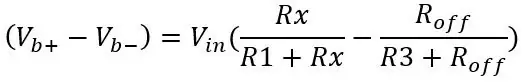
Η τάση εξόδου για το PT100 είναι 80ohms και χρησιμοποιώντας τις άλλες τιμές στην εικόνα:

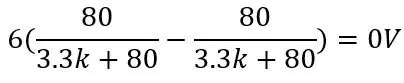
και για το Pt100 να είναι 150ohms:

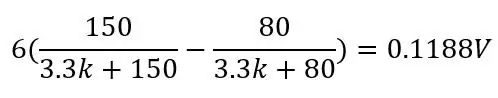
Χρησιμοποιώντας το Wheatstone απαλλαγούμε από τη μετατόπιση DC και αυξάνουμε την ευαισθησία μετά την ενίσχυση. Τώρα που γνωρίζουμε πώς λειτουργεί η γέφυρα Wheatstone μπορούμε να μιλήσουμε για το γιατί χρησιμοποιούμε 80ohms και 3.3kohms. Τα 80ohms εξηγούνται κάπως από τον παραπάνω τύπο, επιλέξτε αυτήν την τιμή (θα την ονομάσουμε αντίσταση μετατόπισης Roff) για να είναι το κάτω εύρος της θερμοκρασίας σας ή ακόμα καλύτερα, ελαφρώς κάτω από το κάτω μέρος της περιοχής σας, εάν χρησιμοποιείται για ένα σύστημα ελέγχου για τη ρύθμιση της θερμοκρασίας ή κάτι τέτοιο, θα θέλατε να μάθετε πόσο χαμηλή είναι η θερμοκρασία κάτω από το εύρος θερμοκρασιών σας. Έτσι, εάν -51.85C είναι το κάτω μέρος της περιοχής σας, χρησιμοποιήστε 74.975 ohms (-65 βαθμούς C) για το Roff σας.

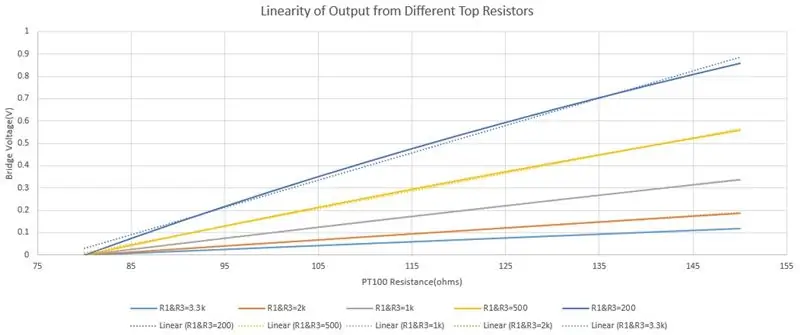
Επέλεξα 3,3k για R1 και R3 για δύο λόγους, για να περιορίσω το ρεύμα και να αυξήσω τη γραμμικότητα της εξόδου. Καθώς το PT100 αλλάζει αντίσταση λόγω θερμοκρασίας, η διέλευση υπερβολικού ρεύματος από αυτό θα δώσει λανθασμένες ενδείξεις λόγω αυτοθέρμανσης, οπότε επέλεξα ένα μέγιστο ρεύμα 5-10mA. Όταν το PT100 είναι 80ohms, το ρεύμα είναι 1,775mA τόσο ασφαλώς κάτω από το μέγιστο εύρος. Μειώνετε την αντίσταση για να αυξήσετε την ευαισθησία, αλλά αυτό θα μπορούσε να έχει αρνητική επίδραση στη γραμμικότητα, καθώς θα χρησιμοποιήσουμε την εξίσωση μιας γραμμής αργότερα (y = mx+c) με μη γραμμική έξοδο θα εισάγει σφάλματα. Η τρίτη εικόνα έχει ένα γράφημα της εξόδου γέφυρας χρησιμοποιώντας διαφορετικές κορυφαίες αντιστάσεις, η σταθερή γραμμή είναι η πραγματική έξοδος και η διακεκομμένη γραμμή είναι η γραμμική προσέγγιση. Μπορείτε να δείτε στο σκούρο μπλε γράφημα (R1 & R3 = 200ohms) δίνει το μεγαλύτερο εύρος τάσης, αλλά η έξοδος είναι η μικρότερη γραμμική. Το γαλάζιο (R1 & R3 = 3.3kohms) δίνει το μικρότερο εύρος τάσης, αλλά η διακεκομμένη γραμμή και η συμπαγής γραμμή επικαλύπτονται, δείχνοντας ότι η γραμμικότητά του είναι πολύ καλή.

Μη διστάσετε να αλλάξετε αυτές τις τιμές ανάλογα με την εφαρμογή σας, επίσης αν αλλάξετε την τάση, βεβαιωθείτε ότι το ρεύμα δεν είναι πολύ υψηλό.

Βήμα 3: Ενίσχυση

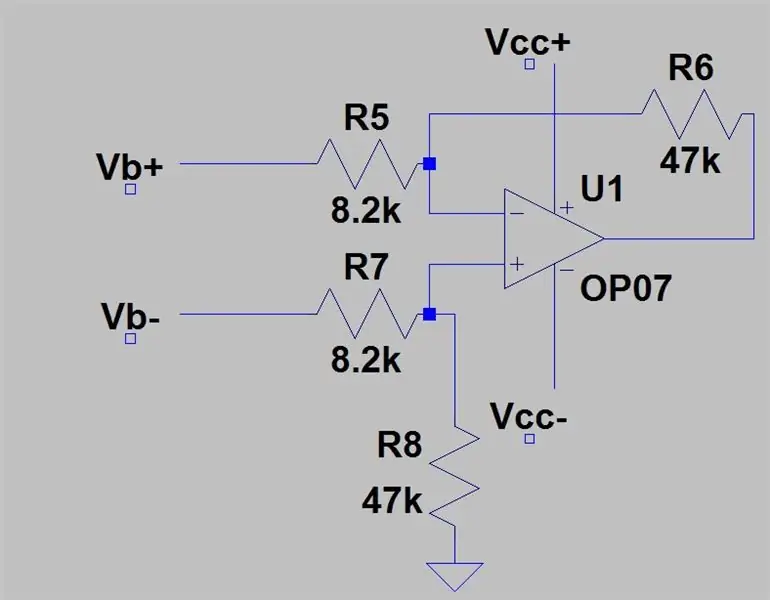
Στο τελευταίο βήμα, βρήκαμε ότι το εύρος εξόδου των δύο διαχωριστών τάσης που αφαιρέθηκε ήταν 0 έως 0.1187 αλλά δεν έχουμε μιλήσει για τον τρόπο αφαίρεσης αυτών των τάσεων. Για να γίνει αυτό θα χρειαστούμε έναν διαφορικό ενισχυτή που θα αφαιρέσει τη μία είσοδο από την άλλη και θα την ενισχύσει με το κέρδος του ενισχυτή. Το κύκλωμα για διαφορικό ενισχυτή φαίνεται στην πρώτη εικόνα. Τροφοδοτείτε το Vb+ στην αναστρέψιμη είσοδο και Vb- στη μη αντιστρεπτή είσοδο και η έξοδος θα είναι η Vb+- Vb- με κέρδος ένα δηλαδή χωρίς ενίσχυση αλλά προσθέτοντας τις αντιστάσεις που φαίνονται στην εικόνα προσθέτουμε κέρδος 5,731 Το Το κέρδος δίνεται από:

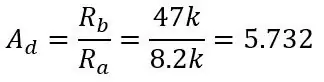
Το Ra είναι R5 & R7 και το Rb είναι R6 & R8, η τάση εξόδου δίνεται από:

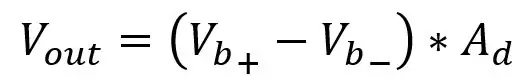
Υπάρχουν δύο προβλήματα με τη σύνδεση μόνο αυτού του ενισχυτή στην έξοδο της γέφυρας, το εφέ φόρτωσης και την αλλαγή του κέρδους. Η αλλαγή του κέρδους του ενισχυτή απαιτεί την αλλαγή τουλάχιστον δύο αντιστάσεων, καθώς τα δύο ζεύγη αντιστάσεων πρέπει να είναι ίδια, οπότε το να έχεις δύο γλάστρες που πρέπει να έχουν την ίδια τιμή θα ήταν ενοχλητικό, οπότε θα χρησιμοποιήσουμε κάτι που ονομάζεται ενισχυτής οργάνων για τα οποία μιλάω παρακάτω. Το φαινόμενο φόρτωσης είναι οι αντιστάσεις εισόδου στον ενισχυτή που επηρεάζουν την πτώση τάσης στο PT100, θέλουμε η τάση στο PT100 να είναι αμετάβλητη και για να το κάνουμε αυτό μπορούμε να επιλέξουμε πολύ μεγάλες αντιστάσεις για τις αντιστάσεις εισόδου έτσι ώστε η παράλληλη αντίσταση του PT100 και η αντίσταση εισόδου είναι πολύ κοντά στην αντίσταση PT100, αλλά αυτό μπορεί να προκαλέσει προβλήματα με τη μετατόπιση θορύβου και τάσης στην οποία δεν πρόκειται να μπω. Απλά επιλέξτε μεσαία εμβέλεια στην περιοχή Kohms, αλλά όπως είπα, το να έχετε μικρές αντιστάσεις είναι επίσης κακό, οπότε θα αλλάξουμε λίγο το κύκλωμα.

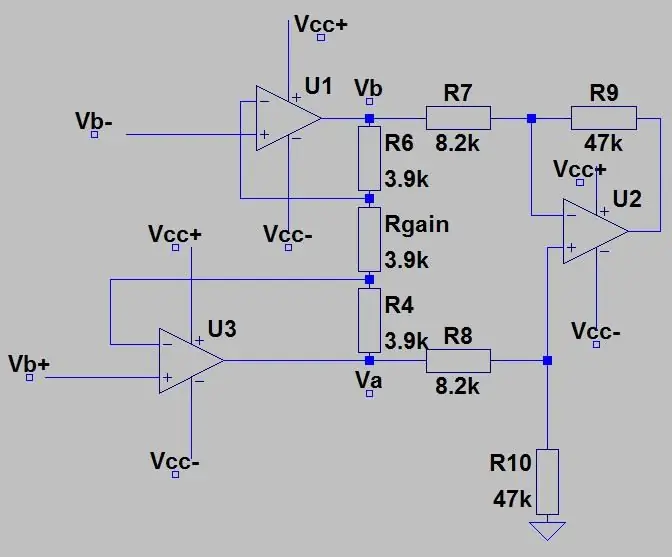
Στη δεύτερη εικόνα, έχουμε την έξοδο της γέφυρας συνδεδεμένη με έναν ενισχυτή οργάνων που λειτουργεί ως ενισχυτής buffer για να διαχωρίσει τα δύο μισά των κυκλωμάτων (γέφυρα και ενίσχυση), καθώς επίσης επιτρέπει τη χρήση για ενίσχυση της εισόδου αλλάζοντας μόνο ένα ποτενσιόμετρο (Ξαναπήρα). Το κέρδος του ενισχυτή οργάνων δίνεται από:

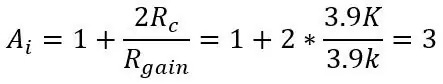
όπου Rc είναι η αντίσταση 3.9k πάνω και κάτω από το δοχείο.

Μειώνοντας το Rgain, η ενίσχυση αυξάνεται. Στη συνέχεια, στο σημείο Va και Vb (ενισχυμένο Vb+ και Vb-), είναι απλώς ένας διαφορικός ενισχυτής όπως πριν και το συνολικό κέρδος του κυκλώματος είναι μόνο τα κέρδη πολλαπλασιασμένα μαζί.

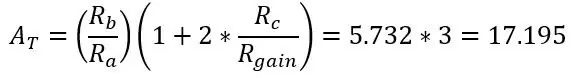
Για να επιλέξετε το κέρδος που θέλετε να κάνετε όπως κάναμε πριν με το Roff, θα πρέπει να επιλέξετε μια αντίσταση ακριβώς πάνω από τη μέγιστη θερμοκρασία σας στο εύρος σας, σε περίπτωση που ξεπεραστεί. Επειδή χρησιμοποιούμε το Arduino που έχει adV 5V, η μέγιστη έξοδος του κυκλώματος πρέπει να είναι 5V στη μέγιστη θερμοκρασία που επιλέξατε. Ας επιλέξουμε τα 150ohms καθώς η μέγιστη αντίσταση και η τάση γέφυρας χωρίς ενίσχυση ήταν 0.1187V, το κέρδος που χρειαζόμαστε είναι 42.185 (5/0.1187)

Ας υποθέσουμε ότι κρατάμε τα Ra, Rb και Rc ως 8,2k, 47k και 3,9k, απλά πρέπει να βρούμε την αξία για το pot Rgain:

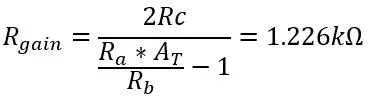
Έτσι, για να βγάλουμε τα πλήρη 5 βολτ από το εύρος θερμοκρασιών που χρησιμοποιούμε, αλλάξτε την τιμή του Rgain σε 1,226k. Η τάση εξόδου που βγαίνει από το διαφορικό ενισχυτή δίνεται από:

Βήμα 4: Τροφοδοσία του κυκλώματος

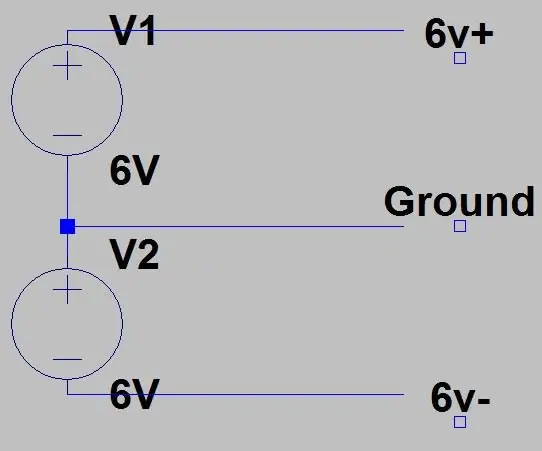
Αυτό είναι το τελευταίο βήμα του κυκλώματος, ίσως παρατηρήσατε τα κυκλώματα Vcc+ και Vcc- στα κυκλώματα ενισχυτή, αυτό συμβαίνει επειδή χρειάζονται θετική και αρνητική τάση για να λειτουργήσουν σωστά, μπορείτε να πάρετε ενιαία ράγα, αλλά αποφάσισα να χρησιμοποιήσω αυτούς τους ενισχυτές καθώς αυτό ήταν που είχα ξαπλωμένο. Έτσι θα παρέχουμε +6V και -6V, υπάρχουν τρεις τρόποι για να το κάνουμε αυτό. Το πρώτο φαίνεται στην πρώτη εικόνα όπου πρέπει να έχουμε δύο τροφοδοτικά ή δύο ακροδέκτες εξόδου από ένα μόνο τροφοδοτικό, να έχουμε και τα δύο στα 6V και να έχουμε τη μία θετική έξοδο συνδεδεμένη με την αρνητική της άλλης. Το 6V της κορυφαίας παροχής θα είναι το +6V μας, το θετικό της κάτω παροχής είναι το GND και το αρνητικό της κάτω παροχής είναι το -6V. ΣΥΝΔΕΤΕ ΜΟΝΟ ΑΚΟΜΑ ΑΝ ΕΙΝΑΙ ΧΩΡΙΣΜΕΝΟΙ ΟΙ ΓΝΔΕΣ ΤΩΝ ΔΥΟ ΠΡΟΜΗΘΕΥΤΩΝ OR ΘΑ ΒΛΑΒΗΣΟΥΝ ΤΗΝ ΠΡΟΜΗΘΕΙΑ ΣΑΣ. Όλα τα εμπορικά τροφοδοτικά θα είχαν χωρισμένα GND, αλλά αν θέλετε να ελέγξετε, χρησιμοποιήστε τον ελεγκτή συνέχειας στο πολύμετρό σας, αν βουίζει, μην χρησιμοποιήσετε αυτήν τη ρύθμιση και χρησιμοποιήστε την επόμενη. Στην σπιτική μου τροφοδοσία, έβγαλα την ασφάλεια κάνοντας αυτό.

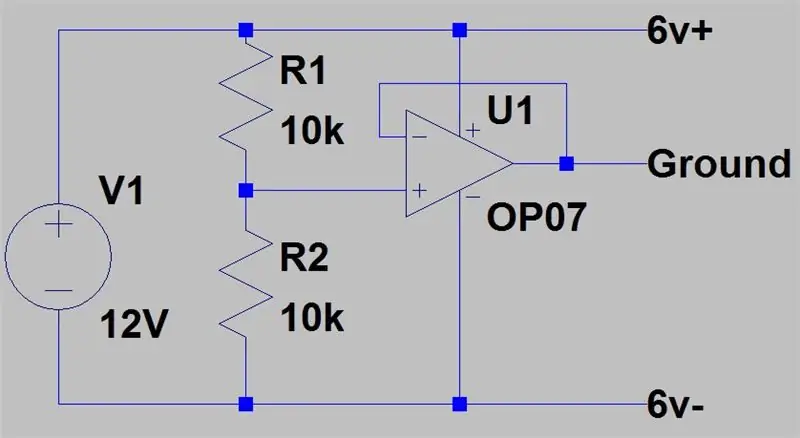
Στη δεύτερη εικόνα είναι η δεύτερη ρύθμιση που μπορούμε να έχουμε, απαιτεί μία τροφοδοσία να έχει διπλή τάση από την άλλη, αλλά δεν θα βλάψει την παροχή εάν είναι συνδεδεμένα τα GND. Έχουμε δύο παροχές, μία στα 12V και άλλη στα 6V. Το 12V θα λειτουργήσει ως το +6V μας, το 6V από τη δεύτερη παροχή θα λειτουργήσει ως GND και τα δύο πραγματικά GND από τα τροφοδοτικά θα λειτουργούν ως -6V.

Αυτή η τελευταία ρύθμιση είναι για τα τροφοδοτικά με μία μόνο έξοδο, χρησιμοποιεί έναν ενισχυτή buffer κέρδους 1 για να δημιουργήσει μια εικονική γείωση περνώντας τη μισή τάση τροφοδοσίας μέσω του ενισχυτή buffer. Στη συνέχεια, το 12V θα λειτουργήσει ως +6V και ο πραγματικός τερματικός σταθμός GND θα είναι -6V.

Εάν θέλετε να χρησιμοποιήσετε μπαταρίες, θα πρότεινα την πρώτη ρύθμιση, αλλά ένα πρόβλημα με τις μπαταρίες είναι ότι η τάση θα μειωθεί καθώς αρχίζουν να πεθαίνουν και η τάση από τη γέφυρα θα μειωθεί επίσης, δίνοντας λάθος ενδείξεις θερμοκρασίας. Θα μπορούσατε φυσικά να διαβάσετε την τάση από τις μπαταρίες και να τις συμπεριλάβετε στους υπολογισμούς ή να χρησιμοποιήσετε ρυθμιστές και περισσότερες μπαταρίες. Στο τέλος, εξαρτάται από εσάς.

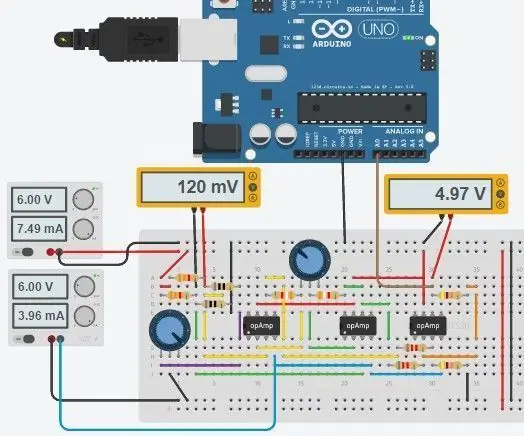
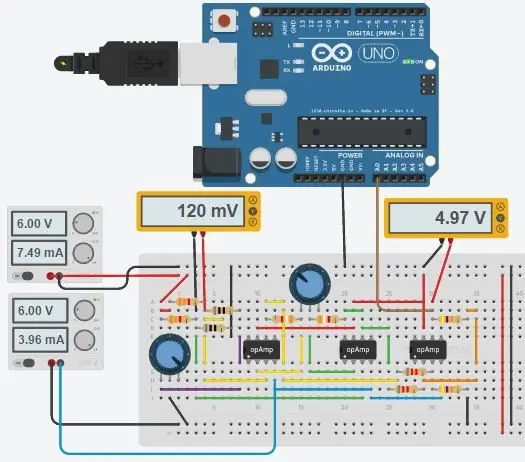
Βήμα 5: Πλήρες κύκλωμα και κωδικός

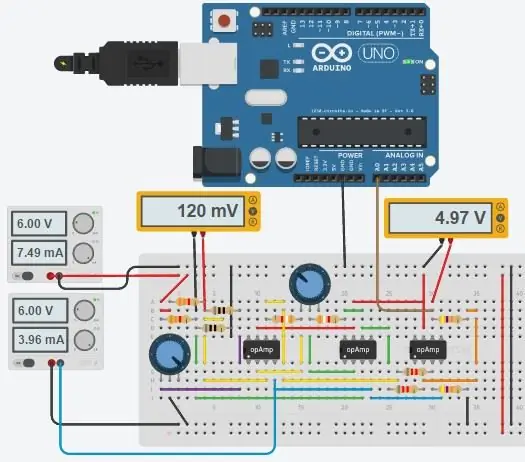
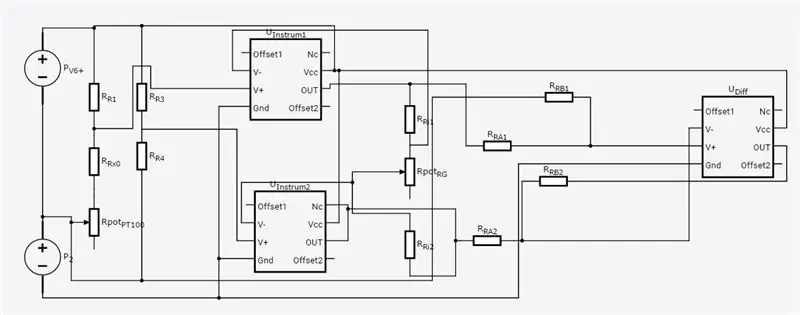
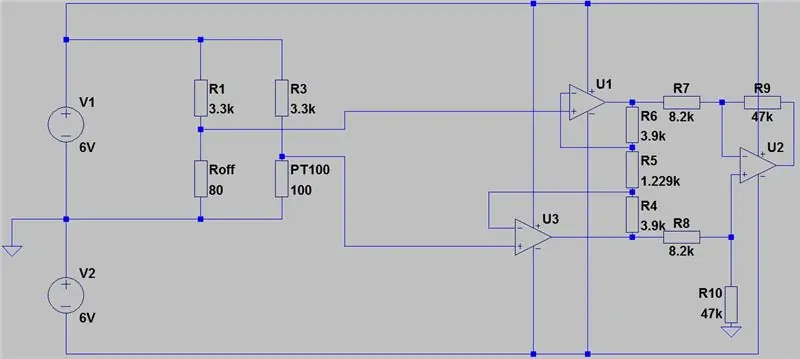
Το πλήρες κύκλωμα φαίνεται παραπάνω και κατασκευάστηκε στο νέο Circuits.io της Autodesk, το οποίο σας επιτρέπει να δημιουργήσετε κυκλώματα στο breadboard, να επεξεργαστείτε το διάγραμμα κυκλώματος (φαίνεται στην εικόνα 2) και τα διαγράμματα PCB και το καλύτερο μέρος, σας επιτρέπει να προσομοιώσετε το κύκλωμα από το breadboard και μπορεί ακόμη και να προγραμματίσει ένα Arduino και να το συνδέσει σε λειτουργία breadboard, πιο κάτω στη σελίδα είναι η προσομοίωση και μπορείτε να παίξετε με δύο γλάστρες. Εάν θέλετε να αντιγράψετε το κύκλωμα και να βάλετε τις δικές σας τιμές, μπορείτε να βρείτε το κύκλωμα εδώ. Το πρώτο δοχείο είναι 70ohms και σε σειρά με αντίσταση 80ohm που προσομοιώνει το PT100 με εύρος 80-150ohms, το δεύτερο δοχείο είναι το κέρδος του ενισχυτή οργάνων. Δυστυχώς χρησιμοποίησα μια βιβλιοθήκη που κατέβασα για τον κωδικό μου, οπότε το Arduino δεν περιλαμβάνεται στο παρακάτω κύκλωμα, αλλά υπάρχουν μόνο δύο επιπλέον καλώδια που πρέπει να συνδέσετε. Εάν είστε πιο άνετα με το LTspice, συμπεριέλαβα ένα αρχείο ανόδου με το κύκλωμα.

Συνδέστε τον ακροδέκτη A0 στην έξοδο του διαφορικού ενισχυτή

Συνδέστε το GND του Arduino στο GND του κυκλώματος (ΟΧΙ ΤΟ -6V)

Και αυτό είναι το κύκλωμα που έγινε, τώρα στον κωδικό. Νωρίτερα ανέφερα ότι θα χρησιμοποιήσουμε τον τύπο y = mx+c, τώρα θα υπολογίσουμε το m (η κλίση) και το c (το offset). Στο Arduino, θα διαβάζουμε τάση, αλλά η εξίσωση θερμοκρασίας χρειάζεται να γνωρίζουμε την αντίσταση του PT100, οπότε ένας τρόπος για να το κάνουμε αυτό είναι να αντικαταστήσουμε το Serial.println (temp) με Serial.println (V) και να καταγράψουμε τάση και αντίσταση σε δύο θερμοκρασίες. Όταν κάνετε αυτήν τη δοκιμή αφήστε το PT100 μόνο για λίγο, για ένα ή δύο λεπτά και κρατήστε το μακριά από οποιεσδήποτε πηγές θερμότητας (ηλιακό φως, ανεμιστήρας φορητού υπολογιστή, το σώμα σας κ.λπ.).

Το πρώτο σημείο που μπορούμε να πάρουμε είναι η θερμοκρασία δωματίου, όταν έχετε συνδέσει το κύκλωμα και δουλεύετε, καταγράψτε την τάση (Vt1) που διαβάστηκε από το Arduino στη σειριακή οθόνη και αποσυνδέστε γρήγορα το PT100 και καταγράψτε την αντίστασή του (Rt1), μην βάζετε βάλτε τον αισθητήρα κατά την αποσύνδεση καθώς αυτό θα αλλάξει την αντίσταση. Για τη δεύτερη θερμοκρασία, θα μπορούσαμε να τοποθετήσουμε τον αισθητήρα σε παγωμένο νερό ή ζεστό νερό (προσέξτε αν χρησιμοποιείτε ζεστό νερό) και να επαναλάβουμε αυτό που κάναμε πριν βρούμε το Vt2 και το Rt2. Ακριβώς αφού τοποθετήσετε τον αισθητήρα στο υγρό περιμένετε ένα λεπτό ή δύο για να κατασταλάξει η αντίσταση. Εάν ενδιαφέρεστε για την απόκριση χρόνου του PT100, καταγράψτε την τάση απενεργοποίησης της σειριακής οθόνης κάθε 2 δευτερόλεπτα περίπου και μπορούμε να βγάλουμε ένα γράφημα από αυτό και θα το εξηγήσω αργότερα. Χρησιμοποιώντας τις δύο τάσεις και αντιστάσεις, μπορούμε να υπολογίσουμε την κλίση ως εξής:

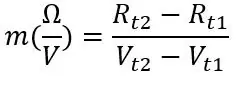
Rt1 και Rt2 είναι οι αντιστάσεις στις δύο θερμοκρασίες και το ίδιο ισχύει για τις τάσεις Vt1 και Vt2. Από την κλίση και ένα από τα δύο σύνολα σημείων που καταγράψατε μπορούμε να υπολογίσουμε την αντιστάθμιση:

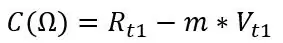
Το C πρέπει να είναι κοντά στο πραγματικό σας Roff, Από την προσομοίωσή μου υπολόγισα αυτές τις τιμές:

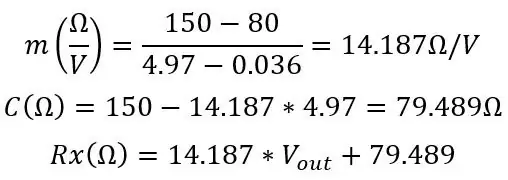
Από αυτήν την αντίσταση μπορούμε να βρούμε τη θερμοκρασία μας χρησιμοποιώντας τον τύπο που είχαμε στην αρχή:

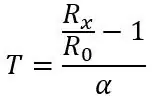
Και αυτό είναι όλο, ο κώδικας για το Arduino είναι παρακάτω, αν έχετε προβλήματα, αφήστε ένα σχόλιο και θα προσπαθήσω να σας βοηθήσω.

Δεν υπάρχουν φωτογραφίες του κυκλώματος που έκανα όπως το έφτιαξα πριν λίγο καιρό και δεν έχω πια το PT100 για να το διασκευάσω και να το δοκιμάσω, αλλά θα πρέπει απλώς να με πιστέψετε ότι λειτουργεί. Δεν υπάρχουν πολλά για το PT100 στο Instructables που βρήκα, γι 'αυτό και έκανα αυτό το ible.

Στο επόμενο βήμα θα μιλήσω για τη χρονική απόκριση του PT100 και εάν δεν σας ενδιαφέρουν τα μαθηματικά, όταν μετράτε μια αλλαγή θερμοκρασίας, αφήστε το PT100 να ηρεμήσει για ένα λεπτό περίπου πριν από την ανάγνωση.

Εάν ενδιαφέρεστε να δείτε άλλα έργα που έχω κάνει, επισκεφθείτε το δικό μου

Ιστολόγιο: Roboroblog

Κανάλι YouTube: Roboro

Or κοιτάξτε τις άλλες οδηγίες μου: εδώ

Εάν το HTML μπερδεύει τον παρακάτω κώδικα, ο κώδικας επισυνάπτεται

* Αυτός ο κωδικός υπολογίζει τη θερμοκρασία χρησιμοποιώντας ένα PT100

* Γράφτηκε από τον Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- Από-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

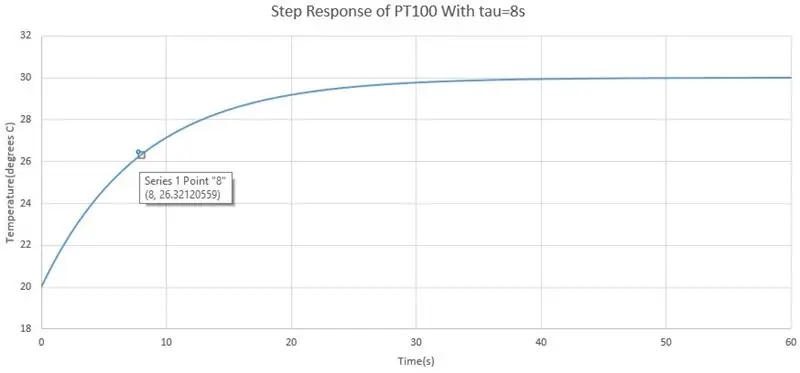
Έτσι ανέφερα ότι το PT100 έχει αργή απόκριση, αλλά μπορούμε να πάρουμε έναν τύπο για την τρέχουσα θερμοκρασία που διαβάζει ο PT100 ανά πάσα στιγμή t. Η απόκριση του PT100 είναι μια απόκριση πρώτης τάξης που μπορεί να γραφτεί με όρους Laplace, δηλαδή συνάρτηση μεταφοράς, όπως:

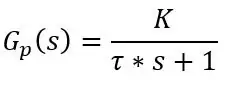
όπου tau (τ) είναι η χρονική σταθερά, K είναι το κέρδος του συστήματος και s είναι ο τελεστής Laplace που μπορεί να γραφτεί ως jω όπου ω είναι η συχνότητα.

Η χρονική σταθερά σας λέει πόσο καιρό χρειάζεται ένα σύστημα πρώτης τάξης για να εγκατασταθεί στη νέα του τιμή και ένας κανόνας ή αντίχειρας είναι ότι το 5*tau είναι πόσος χρόνος θα χρειαστεί για να εγκατασταθεί στη νέα σταθερή κατάσταση. Το κέρδος Κ σας λέει πόσο θα ενισχυθεί η είσοδος. Με το PT100, το κέρδος είναι το πόσο αλλάζει η αντίσταση με τη μεταβολή της θερμοκρασίας, από την επιλογή δύο τυχαίων τιμών από αυτό το φύλλο δεδομένων, πήρα κέρδος 0,3856 ohm/C.

Πριν σας πω ότι μπορείτε να καταγράφετε την τάση κάθε 2 δευτερόλεπτα αφού βάλετε τον αισθητήρα στο υγρό, ζεστό ή κρύο, από αυτό μπορούμε να υπολογίσουμε τη χρονική σταθερά του συστήματος. Πρώτα πρέπει να προσδιορίσετε πού το σημείο εκκίνησης και το τελικό σημείο, το σημείο εκκίνησης είναι η τάση πριν βάλετε τον αισθητήρα στο υγρό και το τελικό σημείο είναι όταν κατακάθισε. Στη συνέχεια αφαιρέστε τα και αυτή είναι η αλλαγή τάσης του βήματος, η δοκιμή που πραγματοποιήσατε ήταν μια αλλαγή βήματος που είναι μια ξαφνική αλλαγή στην είσοδο σε ένα σύστημα, το βήμα είναι η θερμοκρασία. Τώρα στο γράφημα σας μεταβείτε στο 63,2% της αλλαγής τάσης και αυτός ο χρόνος είναι ο σταθερός χρόνος.

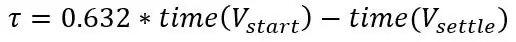
Εάν συνδέσετε αυτήν την τιμή στη συνάρτηση μεταφοράς, τότε έχετε τον τύπο για να περιγράψετε την απόκριση συχνότητας των συστημάτων, αλλά αυτό δεν είναι αυτό που θέλουμε αυτήν τη στιγμή, θέλουμε την πραγματική θερμοκρασία τη στιγμή t για ένα βήμα θερμοκρασίας. να χρειαστεί να πραγματοποιήσετε έναν αντίστροφο μετασχηματισμό Laplace ενός βήματος στο σύστημα. Η συνάρτηση μεταφοράς συστήματος πρώτης τάξης με είσοδο βήματος είναι η ακόλουθη:

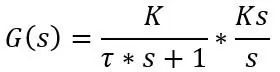
Όπου Ks είναι το μέγεθος του βήματος, δηλαδή η διαφορά θερμοκρασίας. Ας υποθέσουμε ότι ο ανιχνευτής εγκαθίσταται στους 20 βαθμούς C, τοποθετείται στο νερό στους 30 βαθμούς C και ο ανιχνευτής έχει σταθερά χρόνου 8s, η συνάρτηση μεταφοράς και ο τύπος πεδίου χρόνου είναι ο εξής:

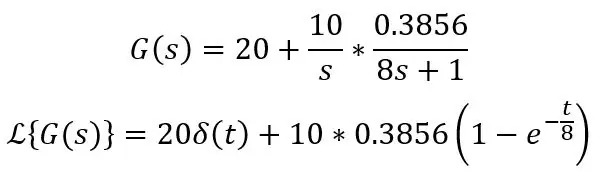
Το δ (t) σημαίνει απλώς μια ώθηση, δηλαδή μετατόπιση DC 20 βαθμών C σε αυτήν την περίπτωση, μπορείτε απλά να γράψετε 20 στις εξισώσεις σας κατά τον υπολογισμό αυτού. Αυτή είναι η τυπική εξίσωση για το βήμα σε ένα σύστημα πρώτης τάξης:

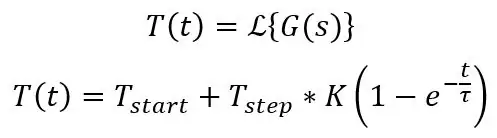
Τα παραπάνω υπολογίζουν τη θερμοκρασία τη χρονική στιγμή t, αλλά αυτό θα λειτουργήσει για την τάση καθώς είναι ανάλογες μεταξύ τους, απλά χρειάζεστε την τιμή εκκίνησης και λήξης, σταθερά χρόνου και μέγεθος βήματος. Ένας ιστότοπος που ονομάζεται Symbolab είναι εξαιρετικός για να ελέγξετε αν τα μαθηματικά σας είναι σωστά, μπορεί να κάνει Laplace, ενσωμάτωση, διαφοροποίηση και πολλά άλλα πράγματα και σας δίνει όλα τα βήματα στην πορεία. Ο αντίστροφος μετασχηματισμός Laplace των παραπάνω μπορεί να βρεθεί εδώ.