Πίνακας περιεχομένων:
- Συγγραφέας John Day day@howwhatproduce.com.
- Public 2024-01-30 08:32.
- Τελευταία τροποποίηση 2025-01-23 14:39.

Σε αυτό το διδακτικό θα εξηγήσω τι είναι ο μέσος όρος λειτουργίας και γιατί πρέπει να τον προσέχετε, καθώς και να σας δείξω πώς πρέπει να εφαρμόζεται για μέγιστη υπολογιστική απόδοση (μην ανησυχείτε για την πολυπλοκότητα, είναι πολύ απλό να το καταλάβετε και θα παρέχετε μια εύχρηστη βιβλιοθήκη και για τα έργα arduino σας:)
Ο μέσος όρος λειτουργίας, επίσης κοινώς αναφερόμενος ως κινητός μέσος όρος, κινητός μέσος όρος ή μέσος όρος, είναι ένας όρος που χρησιμοποιείται για να περιγράψει τη μέση τιμή των τελευταίων τιμών Ν στις σειρές δεδομένων. Μπορεί να υπολογιστεί εξίσου με τον κανονικό μέσο όρο ή μπορείτε να χρησιμοποιήσετε ένα τέχνασμα ώστε να έχει ελάχιστο αντίκτυπο στην απόδοση του κώδικα σας.
Βήμα 1: Περίπτωση χρήσης: Εξομάλυνση μετρήσεων ADC

Το Arduino διαθέτει ένα αξιοπρεπές ADC 10 bit με πολύ μικρό θόρυβο. Κατά τη μέτρηση της τιμής σε έναν αισθητήρα όπως ποτενσιόμετρο, φωτοαντίσταση ή άλλα εξαρτήματα υψηλού θορύβου, είναι δύσκολο να πιστέψουμε ότι η μέτρηση είναι σωστή.
Μια λύση είναι να λαμβάνετε πολλαπλές μετρήσεις κάθε φορά που θέλετε να διαβάζετε τον αισθητήρα σας και να τις υπολογίζετε κατά μέσο όρο. Σε ορισμένες περιπτώσεις αυτή είναι μια βιώσιμη λύση αλλά όχι πάντα. Αν θέλατε να διαβάσετε ADC 1000 φορές ανά δευτερόλεπτο, θα έπρεπε να κάνετε 10 000 αν κάνατε κατά μέσο όρο 10 μετρήσεις. Μια τεράστια σπατάλη χρόνου υπολογισμού.
Η προτεινόμενη λύση μου είναι να λάβω μετρήσεις 1000 φορές το δευτερόλεπτο, να ενημερώσω τον τρέχοντα μέσο όρο κάθε φορά και να τον χρησιμοποιήσω ως τρέχουσα τιμή. Αυτή η μέθοδος εισάγει κάποια καθυστέρηση αλλά μειώνει την υπολογιστική πολυπλοκότητα της εφαρμογής σας, δίνοντάς σας πολύ περισσότερο χρόνο για επιπλέον επεξεργασία.
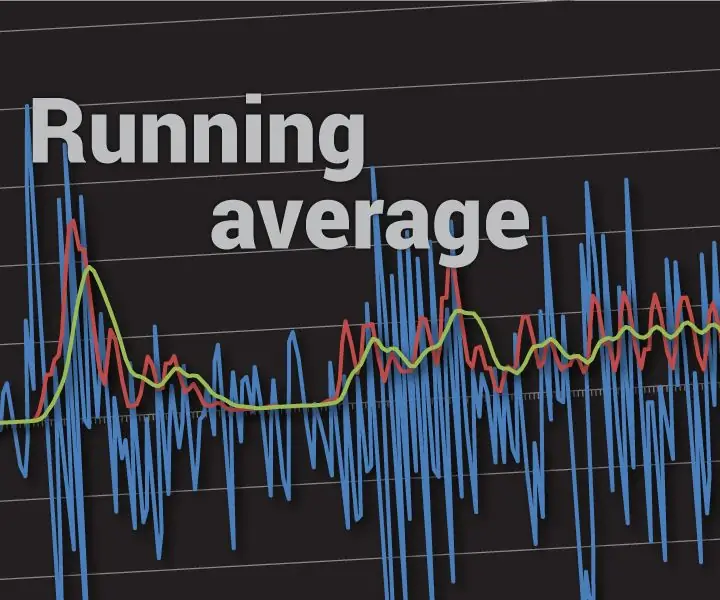
Στην παραπάνω εικόνα χρησιμοποίησα τον μέσο όρο των τελευταίων 32 μετρήσεων. Θα δείτε ότι αυτή η μέθοδος δεν είναι 100% ανθεκτική σε αστοχία, αλλά βελτιώνει σημαντικά την ακρίβεια (δεν είναι χειρότερη από τον μέσο όρο 32 δειγμάτων κάθε φορά). Αν θέλετε να υπολογίσετε κατά μέσο όρο 32 μετρήσεις κάθε φορά, αυτό θα χρειαζόταν πάνω από 0,25 ms στο Arduino UNO μόνο για μετρήσεις!
Βήμα 2: Περίπτωση χρήσης: Μέτρηση εξαρτήματος DC του σήματος μικροφώνου



Το Arduino μπορεί να μετρήσει τάσεις μεταξύ 0 και Vcc (συνήθως 5 V). Το ηχητικό σήμα είναι εντελώς AC και αν θέλετε να το μετρήσετε σε μικροελεγκτή, πρέπει να το κάνετε πόλωση περίπου 1/2 Vcc. Σε ένα έργο Arduino UNO που θα σήμαινε περίπου 2,5 V (DC) + ηχητικό σήμα (AC). Όταν χρησιμοποιείτε τροφοδοτικό 10 bit και 5 V, η προκατάληψη 2,5 V πρέπει να ισούται με 512. Έτσι, για να λάβετε μια τιμή AC σήματος, το 512 πρέπει να αφαιρεθεί από τη μέτρηση ADC και αυτό είναι, σωστά;
Σε έναν ιδανικό κόσμο, αυτό θα ήταν αλήθεια. Δυστυχώς η πραγματική ζωή είναι πιο περίπλοκη και η μεροληψία του σήματος μας τείνει να παρασυρθεί. Πολύ συνηθισμένος είναι ο θόρυβος 50 Hz (60 Hz εάν ζείτε στις ΗΠΑ) από το ηλεκτρικό δίκτυο. Συνήθως δεν είναι πολύ προβληματικό, αλλά είναι καλό να γνωρίζουμε ότι υπάρχει. Πιο προβληματική είναι η γραμμική μετατόπιση από τη θέρμανση των εξαρτημάτων. Ρυθμίζετε προσεκτικά τη διόρθωση μετατόπισης DC στην αρχή και απομακρύνεται αργά καθώς η εφαρμογή σας εκτελείται.
Θα επεξηγήσω αυτό το πρόβλημα με έναν ανιχνευτή κτυπήματος (μουσικής). Ρυθμίζετε την αφαίρεση της προκατάληψης και οι ρυθμοί είναι σαφείς (εικόνα 2). Μετά από κάποιο χρονικό διάστημα, οι κινήσεις μεροληψίας DC και οι παλμοί είναι ελάχιστα αισθητοί στον μικροελεγκτή (εικόνα 3). Ο αλγόριθμος ανίχνευσης παλμών θα διερευνηθεί σε βάθος σε μελλοντικό διδάσκοντα καθώς υπερβαίνει το πεδίο εφαρμογής αυτού του άρθρου.
Ευτυχώς, υπάρχει ένας τρόπος για να συνεχίζετε να υπολογίζετε συνεχώς το offset DC του ήχου. Δεν θα αποτελεί έκπληξη το γεγονός ότι ο μέσος όρος λειτουργίας, θέμα αυτού του διδακτικού, παρέχει μια λύση.
Γνωρίζουμε ότι η μέση τιμή κάθε σήματος AC είναι 0. Χρησιμοποιώντας αυτήν τη γνώση, μπορούμε να αφαιρέσουμε ότι η μέση τιμή του σήματος AC+DC είναι η προκατάληψη DC. Για να το αφαιρέσουμε, μπορούμε να πάρουμε τον τρέχοντα μέσο όρο των τελευταίων τιμών και να τον αφαιρέσουμε από την τρέχουσα ανάγνωση ADC. Σημειώστε ότι πρέπει να χρησιμοποιήσετε αρκετά μεγάλο μέσο όρο λειτουργίας. Για τον ήχο, ένα δέκατο του δευτερολέπτου (ο αριθμός των δειγμάτων εξαρτάται από τον ρυθμό δειγματοληψίας σας) πρέπει να είναι αρκετό, αλλά να γνωρίζετε ότι οι μέσοι όροι μεγαλύτερης διάρκειας λειτουργούν καλύτερα. Στην πρώτη εικόνα μπορείτε να δείτε παράδειγμα πραγματικού υπολογισμού πόλωσης DC με μέσο όρο λειτουργίας με 64 στοιχεία σε ρυθμό δείγματος 1 kHz (λιγότερο από ό, τι συνιστούσα, αλλά εξακολουθεί να λειτουργεί).
Βήμα 3: Υπολογισμός

Μπορείτε να φανταστείτε το μέσο τρέξιμο ως μέσο όρο βάρους των ατόμων στην αίθουσα αναμονής του γιατρού. Ο γιατρός ολοκληρώνει την εξέταση ενός ασθενούς και ταυτόχρονα ένας νέος μπαίνει στην αίθουσα αναμονής.
Για να μάθει το μέσο βάρος όλων των ασθενών που περιμένουν στην αίθουσα αναμονής, η νοσοκόμα θα μπορούσε στη συνέχεια να ρωτήσει κάθε ασθενή για το βάρος τους, να προσθέσει αυτούς τους αριθμούς και να διαιρέσει με τον αριθμό των ασθενών. Κάθε φορά που ο γιατρός δέχεται νέο ασθενή, η νοσοκόμα επαναλάμβανε ολόκληρη τη διαδικασία.
Mightσως να σκέφτεστε: "Αυτό δεν ακούγεται πολύ αποδοτικό … Πρέπει να υπάρχει καλύτερος τρόπος για να γίνει αυτό." Και θα είχες δίκιο.
Για τη βελτιστοποίηση αυτής της διαδικασίας, η νοσοκόμα θα μπορούσε να τηρεί αρχείο συνολικού βάρους της τρέχουσας ομάδας ασθενών. Μόλις ο γιατρός καλέσει τον νέο ασθενή, η νοσοκόμα τον ρωτούσε για το βάρος του και το αφαιρούσε από το σύνολο της ομάδας και τον άφηνε να φύγει. Ο νοσηλευτής ρωτούσε τον ασθενή που μόλις μπήκε στην αίθουσα αναμονής για το βάρος του και το πρόσθεσε στο σύνολο. Το μέσο βάρος των ασθενών μετά από κάθε βάρδια θα ήταν το άθροισμα των βαρών διαιρούμενο με τον αριθμό των ασθενών (ναι, όπως και πριν, αλλά τώρα η νοσοκόμα ρώτησε μόνο δύο άτομα για το βάρος τους αντί για όλους). Συνειδητοποιώ ότι αυτή η παράγραφος μπορεί να ήταν λίγο συγκεχυμένη, οπότε δείτε την παραπάνω εικόνα για επιπλέον σαφήνεια (ή κάντε ερωτήσεις στα σχόλια).
Αλλά ακόμα κι αν δεν βρήκατε την τελευταία παράγραφο μπερδεμένη, μπορεί να έχετε ερωτήσεις όπως τι πρέπει να υπάρχει στο συσσωρευτή στην αρχή, πώς μπορώ να βάλω αυτό που μόλις διάβασα σε έναν πραγματικό κωδικό C; Αυτό θα αντιμετωπιστεί στο επόμενο βήμα, όπου θα λάβετε επίσης τον πηγαίο μου κώδικα.
Βήμα 4: Ο κώδικας

Για να υπολογίσετε τον μέσο όρο λειτουργίας, χρειάζεστε πρώτα έναν τρόπο αποθήκευσης των τελευταίων τιμών Ν. θα μπορούσατε να έχετε έναν πίνακα με στοιχεία N και να μετακινείτε ολόκληρο το περιεχόμενο σε ένα μέρος κάθε φορά που προσθέτετε ένα στοιχείο (παρακαλώ μην το κάνετε αυτό) ή μπορείτε να αντικαταστήσετε ένα παλιό στοιχείο και να προσαρμόσετε τον δείκτη στο επόμενο στοιχείο που θα πεταχτεί έξω (κάντε το:)
Ο συσσωρευτής πρέπει να αρχίσει να αρχίζει στο 0, το ίδιο ισχύει για όλα τα στοιχεία στη γραμμή καθυστέρησης. Σε άλλη περίπτωση, ο μέσος όρος λειτουργίας σας θα είναι πάντα λάθος. Θα δείτε ότι το delayLine_init φροντίζει για την αρχικοποίηση της γραμμής καθυστέρησης, θα πρέπει να φροντίσετε μόνοι σας τον συσσωρευτή.
η προσθήκη ενός στοιχείου στη γραμμή καθυστέρησης είναι τόσο εύκολη όσο η μείωση του δείκτη του νεότερου στοιχείου κατά 1, βεβαιωθείτε ότι δεν δείχνει την πλευρά του πίνακα γραμμών καθυστέρησης. μετά τη μείωση του δείκτη όταν είναι 0, θα κυκλώσει γύρω στο 255 (επειδή είναι ένας ακέραιος ακέραιος αριθμός 8 bit). Ο τελεστής Modulo (%) με το μέγεθος του πίνακα γραμμών καθυστέρησης θα διασφαλίσει ότι το ευρετήριο θα δείχνει ένα έγκυρο στοιχείο.
Ο υπολογισμός του μέσου όρου λειτουργίας πρέπει να είναι εύκολα κατανοητός εάν ακολουθήσατε την αναλογία μου στο προηγούμενο βήμα. Αφαιρέστε το παλαιότερο στοιχείο από τον συσσωρευτή, προσθέστε τη νεότερη τιμή στον συσσωρευτή, σπρώξτε τη νεότερη τιμή στη γραμμή καθυστέρησης, επιστρέψτε τον συσσωρευτή διαιρούμενο με τον αριθμό στοιχείων.
Εύκολο, σωστά;
Μη διστάσετε να πειραματιστείτε χρησιμοποιώντας τον συνημμένο κώδικα για να καταλάβετε καλύτερα πώς λειτουργεί όλο αυτό. Όπως είναι σήμερα, το arduino διαβάζει αναλογική τιμή στον αναλογικό πείρο A0 και εκτυπώνει "[τιμή ADC], [μέσος όρος λειτουργίας]" στη σειριακή θύρα με ρυθμό 115200 baud. Εάν ανοίξετε το σειριακό plotter του arduino με το σωστό ρυθμό baud, θα δείτε δύο γραμμές: τιμή ADC (μπλε) και εξομάλυνση τιμής (κόκκινο).
Βήμα 5: Επιπλέον

Υπάρχουν μερικά πράγματα που δεν χρειάζεται απαραίτητα να γνωρίζετε για να χρησιμοποιήσετε τον μέσο όρο στο έργο σας και δεν θα βλάψετε να τα γνωρίζετε.
καθυστέρηση: Θα ξεκινήσω μιλώντας για την απεικόνιση αυτού του βήματος. Θα παρατηρήσετε ότι ο τρέχων μέσος όρος περισσότερων στοιχείων εισάγει μεγαλύτερη καθυστέρηση. Εάν ο χρόνος απόκρισης για αλλαγή στην τιμή είναι κρίσιμος, ίσως θελήσετε να χρησιμοποιήσετε μικρότερο μέσο όρο λειτουργίας ή να αυξήσετε το δείγμα (μετρήστε πιο συχνά).
Προχωράω.
προετοιμασία: Όταν μίλησα για αρχικοποίηση στοιχείων συσσωρευτή και καθυστέρησης, είπα ότι πρέπει να τα αρχικοποιήσετε όλα στο 0. Εναλλακτικά, μπορείτε να αρχικοποιήσετε τη γραμμή καθυστέρησης σε οτιδήποτε σας αρέσει, αλλά ο συσσωρευτής θα πρέπει να ξεκινά ως άθροισμα των νεότερων Ν στοιχείων στη γραμμή καθυστέρησης (όπου Ν είναι αριθμός στοιχείων στο μέσο τρέξιμό σας). Εάν ο συσσωρευτής ξεκινήσει με οποιαδήποτε άλλη τιμή, ο υπολογισμένος μέσος όρος θα είναι λάθος - είτε πολύ χαμηλός είτε πολύ υψηλός, πάντα κατά το ίδιο ποσό (υποθέτοντας τις ίδιες αρχικές συνθήκες). Σας προτείνω να προσπαθήσετε να μάθετε γιατί συμβαίνει αυτό χρησιμοποιώντας κάποια "προσομοίωση στυλό και χαρτιού".
μέγεθος συσσωρευτή: Θα πρέπει επίσης να σημειώσετε ότι ο συσσωρευτής θα πρέπει να είναι αρκετά μεγάλος για να αποθηκεύει το άθροισμα όλων των στοιχείων στη γραμμή καθυστέρησης εάν είναι όλα θετικά ή αρνητικά max. Πρακτικά αυτό σημαίνει ότι ο συσσωρευτής πρέπει να είναι ένας τύπος δεδομένων μεγαλύτερος από τα στοιχεία γραμμής καθυστέρησης και να είναι υπογεγραμμένος, εάν υπογραφούν στοιχεία γραμμής καθυστέρησης.
κόλπο: Οι γραμμές μεγάλης καθυστέρησης καταλαμβάνουν πολλή μνήμη. Αυτό μπορεί γρήγορα να γίνει πρόβλημα. Εάν η μνήμη σας είναι πολύ περιορισμένη και δεν σας ενδιαφέρει ιδιαίτερα η ακρίβεια, μπορείτε να προσεγγίσετε τον μέσο όρο λειτουργίας, παραλείποντας εντελώς την καθυστέρηση και κάνοντας το αντ 'αυτού: αφαιρέστε τον συσσωρευτή 1/N * από τον συσσωρευτή και προσθέστε νέα τιμή (σε παράδειγμα 8 μέσους χρόνους λειτουργίας: συσσωρευτής = συσσωρευτής * 7/8 + newValue). Αυτή η μέθοδος δίνει λάθος αποτελέσματα, αλλά είναι μια αξιοπρεπής μέθοδος υπολογισμού του μέσου όρου λειτουργίας όταν έχετε χαμηλή μνήμη.
γλωσσολογία: ο "μέσος όρος/μέσος όρος" χρησιμοποιείται συνήθως όταν αναφέρεται σε μέσους όρους σε πραγματικό χρόνο, ενώ ο "κινούμενος μέσος όρος/μέσος όρος" συνήθως σημαίνει ότι ο αλγόριθμος λειτουργεί σε σύνολο στατικών δεδομένων, όπως το υπολογιστικό φύλλο excel.
Βήμα 6: Συμπέρασμα
Ελπίζω ότι αυτό το διδακτικό ήταν αρκετά εύκολο να κατανοηθεί και ότι θα σας βοηθήσει στα μελλοντικά σας έργα. Μη διστάσετε να δημοσιεύσετε ερωτήσεις στα παρακάτω σχόλια εάν υπάρχει κάτι ασαφές.
Συνιστάται:
Σταθμισμένος μέσος όρος CP2 Excel: 14 βήματα
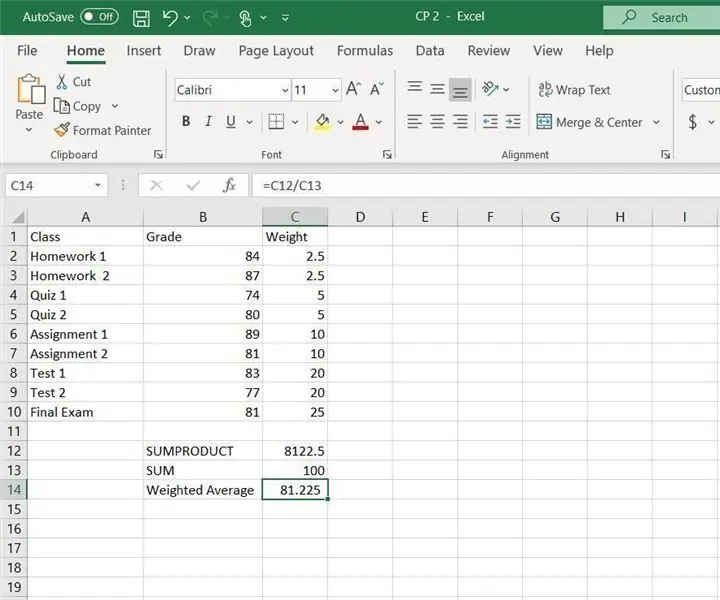
Σταθμισμένος μέσος όρος CP2 Excel: Οδηγίες για τον τρόπο υπολογισμού του σταθμισμένου μέσου όρου στο Excel. Σε αυτό το παράδειγμα, η συνάρτηση SUMPRODUCT και SUM θα χρησιμοποιηθούν στο Excel. Ο σταθμισμένος μέσος όρος είναι χρήσιμος για τον υπολογισμό του συνολικού βαθμού για μια τάξη
Δημιουργήστε τη δική σας εντολή εκτέλεσης με εύκολο βήμα: 4 βήματα
Δημιουργήστε τη δική σας εντολή εκτέλεσης με εύκολο βήμα: Εδώ θα δείξω πώς μπορείτε να δημιουργήσετε τη δική σας εντολή εκτέλεσης στο λειτουργικό σύστημα Windows. Στην πραγματικότητα, αυτή η δυνατότητα στα παράθυρα είναι εξαιρετική, η οποία είναι χρήσιμη για να ανοίξετε αμέσως το παράθυρο της εφαρμογής σας. Έτσι, τώρα μπορείτε επίσης να δημιουργήσετε την εντολή σας για να ανοίξετε οποιαδήποτε εφαρμογή εισάγοντας
10 βασικά έργα Arduino για αρχάριους! Κάντε τουλάχιστον 15 έργα με έναν πίνακα!: 6 βήματα

10 βασικά έργα Arduino για αρχάριους! Κάντε τουλάχιστον 15 έργα με έναν μόνο πίνακα !: Arduino Project & Φροντιστήριο Περιλαμβάνει 10 βασικά έργα Arduino. Όλοι οι πηγαίοι κώδικες, το αρχείο Gerber και άλλα. Όχι SMD! Εύκολη συγκόλληση για όλους. Εύκολα αφαιρούμενα και αντικαταστάσιμα εξαρτήματα. Μπορείτε να κάνετε τουλάχιστον 15 έργα με ένα μόνο bo
Αυξήστε την χωρητικότητα (χρόνος εκτέλεσης) της μπαταρίας του φορητού υπολογιστή σας .: 6 βήματα

Αυξήστε την χωρητικότητα (χρόνος εκτέλεσης) της μπαταρίας του φορητού υπολογιστή σας: Η μπαταρία του φορητού υπολογιστή σας είναι νεκρή; Ο χρόνος εκτέλεσης δεν είναι αρκετός για να σας ξεπεράσει την ημέρα; Έχετε ένα από αυτά τα τεράστια εξωτερικά πακέτα μπαταριών; Αυτό το εκπαιδευτικό έχει σκοπό να δείξει πώς μπορεί κάποιος να αντικαταστήσει τα νεκρά κύτταρα ιόντων λι-ιόντων/λι-πολυ ενός φορητού υπολογιστή
Αυτόνομο Όρος για Astro Photography: 4 Βήματα (με Εικόνες)

Αυτόνομο στήριγμα για φωτογράφιση Astro: Αυτό το μικρό στήριγμα επιτρέπει σε μια κάμερα φωτός να ακολουθεί τα αστέρια καθώς κινούνται στον ουρανό. Οι χρόνοι έκθεσης ενός λεπτού δεν αποτελούν πρόβλημα. Για να αποκτήσετε υπέροχες αστρο φωτογραφίες μπορείτε να στοιβάζετε αρκετές εικόνες. Απαιτούνται υλικά: Ηλεκτρομηχανικά χρονόμετρα μικρό τρίποδο, στο l
